Теоретические введения

Дифракция света – явление, наблюдаемое при распространении света в среде вблизи непрозрачных тел сквозь малые отверстия и связанное с отклонениями от законов геометрической оптики.

Дифракция приводит к огибанию световыми волнами препятствий и проникновению света в область геометрической тени.

Дифракция легко наблюдается, если размеры преграды, например, щели, через которую проходит свет, соизмеримы с длиной волны в пределах нескольких порядков.

Дифракцию объясняет принцип Гюйгенса – именно вторичные волны огибают препятствия на пути распространения первичных волн.

Френель дополнил принцип Гюйгенса представлением о когерентности вторичных волн и их интерференции.

Явление интерференции свидетельствует о том, что свет – волна.

Интерференцией световых волн называется сложение двух или более когерентных волн, вследствие которого наблюдается усиление или ослабление результирующих световых колебаний в различных точках пространства.

Когерентностью называется согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов. В простейшем случае когерентными являются волны одинаковой длины, между которыми существует постоянная разность фаз.

Все источники света, кроме лазера, некогерентны.

Монохроматическое излучение (греч. mono – один и chroma (родительный падеж chromatos) – цвет) – электромагнитное излучение, обладающее очень малым разбросом частот, в идеале – одной длиной волны. Монохроматическое излучение формируется в системах, в которых существует только один разрешённый электронный переход из возбуждённого в основное состояние. На практике используют несколько способов получения монохромного излучения: призматические системы для выделения потока излучения с заданной степенью монохроматичности; системы на основе дифракционной решетки; лазеры, излучение которых не только высокомонохроматично, но и когерентно; газоразрядные лампы и другие источники света, в которых происходит преимущественно один электронный переход (например, натриевая лампа, в излучении которой преобладает наиболее яркая линия D или ртутная лампа).

Монохроматические волны – неограниченные в пространстве волны одной определенной и постоянной частоты – являются когерентными.

Для получения монохроматического излучения используются оптические квантовые генераторы (ОКГ) – источники света, работающие на основе эффекта вынужденного излучения в активной среде с инверсной населённостью энергетических уровней. ОКГ, работающие в оптическом диапазоне, называются лазерами. ОКГ, работающие в диапазоне ультракоротких волн, называются мазерами.

Существует несколько типов лазеров: твёрдотельные, газовые, полупроводниковые и жидкостные (в основу такого деления положен тип активной среды). Лазеры также классифицируются по методу накачки: оптические, тепловые, химические, электроионизационные и др. Различают непрерывный и импульсный режимы генерации лазера.

Лазер как источник света качественно отличается от обычных, нелазерных источников. Для излучения лазера характерны: а) острая направленность, очень малое угловое расхождение в пучке; б) большая яркость (большая плотность потока энергии); в) временная и пространственная когерентность; г) строгая монохроматичность;

Лазер излучает узкий, малорасходящийся световой пучок. В случае теплового источника узкий пучок можно получить с помощью экрана с малым отверстием. Однако яркость лазера значительно больше, чем у обычного нелазерного источника света

Согласно принципу Гюйгенса-Френеля, световая волна, возбуждаемая каким-либо источником S, может быть представлена как результат суперпозиции (сложения) когерентных вторичных волн, излучаемых вторичными (фиктивными) источниками – бесконечно малыми элементами любой замкнутой поверхности, охватывающей источник S.

В зависимости от схемы наблюдения дифракционные явления условно разделяют на дифракцию Френеля (рис. 1.1.) и дифракцию Фраунгофера (рис. 1.2.).

Дифракция Френеля (дифракция в расходящихся лучах)	Дифракция Фраунгофера (дифракция в параллельных лучах)
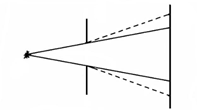Рис.1.1. Дифракция Френеля	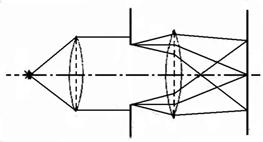Рис.1.2. Дифракция Фраунгофера: 1 – источник света; 2 – щель; 3 и 4 – линзы; 5 – дифрагированные лучи; 6 – фокальная плоскость
На препятствие падает сферическая или плоская волна	На препятствие падает плоская волна
Дифракционная картина наблюдается на экране, находящемся позади препятствия на конечном расстоянии от него	Дифракционная картина наблюдается на экране, который находится в фокальной плоскости собирающей линзы, установленной на пути прошедшего через препятствие света
На экране получается «дифракционное изображение» препятствия	На экране получается «дифракционное изображение» удаленного источника света

Зоны Френеля

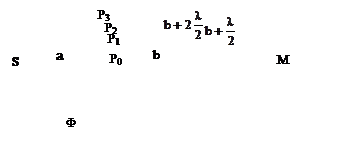
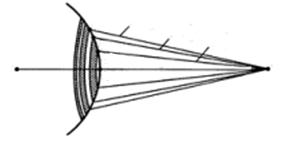
Рис. 1.3. Разбивка сферической волновой поверхности на кольцевые зоны Френеля

Согласно принципу Гюйгенса-Френеля, заменим действие источника S действием воображаемых источников, расположенных на вспомогательной поверхности Ф, являющейся поверхностью фронта волны, идущей из S (поверхность сферы с центром S).

Разобьем волновую поверхность Ф на кольцевые зоны такого размера, чтобы расстояния от краев зоны до M отличались на λ/2. Тогда, обозначив амплитуды колебаний от 1-й, 2-й, … m-й зон через A₁, A₂, … A_m (при этом A₁ > A₂ > A₃ >…), получим амплитуду результирующего колебания: A = A₁ – A₂ + A₃ – A₄ +…

При таком разбиении волновой поверхности на зоны оказывается, что амплитуда колебания A_m от некоторой m-й зоны Френеля равна среднему арифметическому от амплитуд примыкающих к ней зон

.

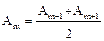Тогда результирующая амплитуда в точке M будет:

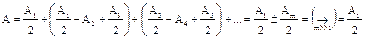, (1.1)

так как при m>>1 A₁>>A_m.

Таким образом, амплитуда результирующих колебаний в произвольной точке М определяется действием только половины от амплитуды центральной зоны Френеля.

Площади всех зон Френеля:

,

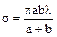где a – длина отрезка SP₀, являющегося радиусом сферы Ф, b – длина отрезка P₀M.

Радиус внешней границы m-й зоны Френеля:

.

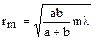Date: 2015-05-05; view: 412; Нарушение авторских прав