Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Варіант№10
|
|
1. Розв’язати систему лінійних рівнянь методом Гаусса, за формулами Крамера, матричним способом.а)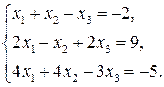 
2.Обчислити визначник 
(методом зведення до трикутної форми; шляхом розкладу за елементами рядка або стовпця).
3.Встановити парність підстановки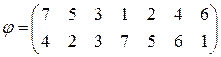 
4.Довести, що відношення х ділиться 
на у в множині М12 є нестрогим порядком.
5.Знайти дійсну та уявну частини комплексних чисел
а) (2-4і)3+(2+4і)3; б)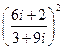 
6. Розв’язати рівняння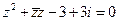 
7.Використовуючи тригонометричну форму комплексного числа, обчислити: а)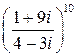 
; б)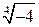 
.
8.Знайти всі значення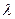 
при яких вектор 
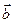(5,-3, 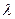) лінійно виражається через вектори 
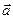1(2,3,5), 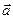2(1,5,8), 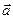3(1,-4,1).
9.Знайти деякий базис системи векторів і виразити через цей базис інші вектори, якщо 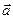1(2,-1,3,4), 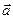2(1,2,-3,1), 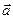3(5,-5,12,11), 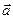4(1,-3,6,3).
10.Знайти ранг матриці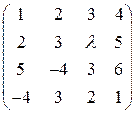 
в залежності від значень параметра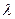
11.Дослідити систему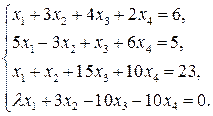 
і знайти загальний розв’язок в залежності від значення параметра .
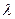12.Знайти при якому значенні 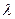система 
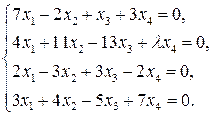лінійних однорідних рівнянь має ненульові розв’язки. Розв’язати її при знайдених значеннях .
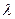Date: 2015-04-23; view: 549; Нарушение авторских прав