Плотность энергетических уровней

Для того чтобы знать, как распределяются по энергиям электроны в кристалле, надо установить, как распределены внутри зон разрешенные квантовые состояния, а во-вторых, как они заполняются электронами, т.е. вероятность их заполнения.

Концентрацию электронов, имеющих энергии, заключенные в интервале от Е до Е+dЕ, можно представить так:

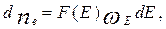
где 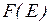– функция плотности энергетических состояний;

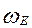– вероятность заполнения энергетических уровней зарядоносите-

лями.

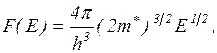
где 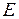– энергия электрона, отсчитанная от границы зоны;

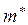– эффективная масса электрона, учитывающая энергетическую

связь его с полями частиц кристалла;

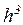– элементарная ячейка пространства импульсов.

Электронный газ в металлах всегда вырожден. Реальные температуры катодов около 2000° С. В этом случае используют распределение Ферми-Дирака:

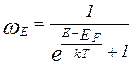, (1)

где 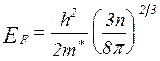– энергия или уровень Ферми.

При этом уравнение концентрации электронов принимает вид:

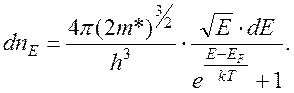
Проанализируем это уравнение. При Т = О и Е > Е_F первый член знаменателя обращается в бесконечность, а вероятность заполнения электронами энергетических уровней (W_E) и соответственно вся правая часть уравнения оказывается равной нулю.

Следовательно, при температуре абсолютного нуля в металле нет электронов с энергией больше Е_F.

При Т = О и Е < Е_F первый член знаменателя - нуль, вероятность заполнения электронами энергетических уровней (W_E) оказывается равной единице и кривая распределения электронов по энергиям (кривая Т=0 на рис. 2.10) представляет собой обратную параболу.

Итак, у металлов константа Е_F имеет простой и наглядный физический смысл: это наибольшая энергия, которой обладают электроны при температуре абсолютного нуля.

При Т > О и Е = Е_F получим 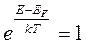и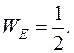

В результате приходим к очень важному для последующего изложения выводу, применимому не только к металлам, но также к диэлектрикам и полупроводникам: уровень Ферми – это такой уровень, вероятность заполнения которого электронами при любых температурах равна 1/2.

При Т > О и Е < Е_F величина (W_E) несколько меньше единицы. Вместе с тем для энергий Е > Е_F появляется некоторая отличная от нуля вероятность заполнения энергетических уровней. Распределение валентных электронов металла по энергиям при Т > О соответствует кривой на рис. 2.10.

Рис. 2.10 – Распределение электронов по энергиям в металле

Вопросы распределения по энергиям носителей заряда в полупроводниках будут рассматриваться позднее. Мы же остановимся на вопросе расположения уровня Ферми в кристаллах.

В проводниках уровень Ферми располагается на уровне перехода из зоны проводимости в валентную зону.

У диэлектриков и собственных полупроводников уровень Ферми располагается в середине запрещенной зоны и практически не зависит от температуры.

У донорного полупроводника уровень Ферми при Т = О располагается посередине между донорным уровнем и дном зоны проводимости, а при повышении температуры он смещается вниз, причем тем сильнее, чем меньше концентрация донорной примеси.

У дырочного полупроводника уровень Ферми при Т = О располагается посередине между акцепторным уровнем и потолком валентной зоны, а при повышении температуры он смещается вверх, причем тем сильнее, чем меньше концентрация акцепторов.

Date: 2015-05-04; view: 906; Нарушение авторских прав