Вронскиан. Линейная зависимость и независимость функций

Определителем Вронского W(x; y ₁(x), y ₂(x),..., y_n (x)) называется определитель, первая строка которого образована функциями y ₁(x), y ₂(x),..., y_n (x) из C _{n -1}[ a, b ], а последующие строки образованы производными от функций предыдущей строки:

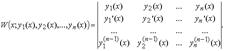
Если определитель этой матрицы равен нулю то функция линейна зависима. Если функция не равна нулю то функция независима.

13.

14. Определение. Числовой ряд наз. сходящимся если существует конечный предел n-ной частичной суммы, где S – сумма ряда

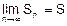
Если при этом предел =∞ или не существует то ряд (1) расходится

Необходимое условие сходимости ряда: Если ряд (1) сходится, то предел

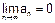
Доказательство:

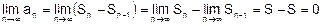
Стоит заметить, что если условие выполняется ряд может как сходиться, так и расходиться, если же оно не выполняется – то ряд расходится.

15.. Ряды с положительными членами. Признаки сравнения, пр. Даламбера.

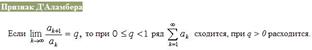
При́знак д’Аламбе́ра (или Признак Даламбера) — признак сходимости числовых рядов, установлен Жаном д’Аламбером в 1768 г.

Если для числового ряда

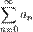
существует такое число 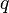, , 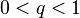что, начиная с некоторого номера, выполняется неравенство

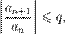
то данный ряд абсолютно сходится; если же, начиная с некоторого номера

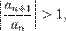то ряд расходится.

16. Интегральный признак Коши́ – Макло́рена — признак сходимости убывающего положительного числового ряда. Признак Коши – Маклорена даёт возможность свести проверку сходимости ряда к проверке сходимости несобственного интеграла соответствующей функции на 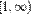, последний часто может быть найден в явном виде.

Радикальный признак Коши — признак сходимости числового ряда:

Если для числового ряда

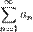
с неотрицательными членами существует такое число 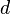, , 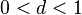что, начиная с некоторого номера, выполняется неравенство 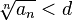, то данный ряд сходится.

17. Степенные ряды: Ряд вида

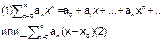
где 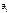- числа, , называется степенным рядом.

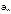-коэффициент данного ряда

Теорема Абеля: если степенной ряд (1) сх при 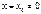, то (1) сх для всех 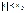т.е (–|x0|;|x0|)

И если ряд (1) расх при 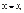, то степенной ряд (1) расх для всех 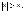т.е (-∞;-|x1|)U(|x1|;+ ∞)

Структура области сходимости степенного ряда

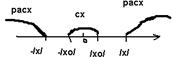
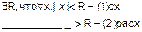
R-радиус сходимости

(-R;R) – инт-л сход-ти.

Инт-л, в кот включ. Или не включ. концы рядов наз областью сходимости.

Радиус сх-ти степ. Ряда:

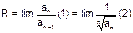
(1) – по признаку Даламбера

(2) - по радикальн. признаку Коши

Date: 2015-06-08; view: 684; Нарушение авторских прав