Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Метод моментов для точечной оценки параметров распределения
|
|
Предполагаем, что известен вид функции распределения исследуемой случайной величины (например, равномерное дискретное, или непрерывное экспоненциальное или нормальное и т.д.).
Для определения неизвестных параметров этого известного распределения составляем уравнения, в левой части которых – теоретические, а в правых – эмпирические моменты одинаковых порядков. Число таких уравнений равно числу неизвестных параметров распределения (для равномерного -2, для показательного – 1, для нормального – 2 и т. д.)
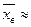
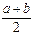; DB 
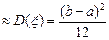для равномерного;
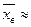a; DB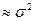 
для нормального;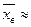 
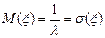для экспоненциалього.
Метод наибольшего правдоподобия для точечной оценки параметров распределения.
Составляем функцию правдоподобия дискретной случайной величины, аргументы которой – полученные выборочным методом значения случайной величины и оцениваемый параметр распределения. Исследуем эту функцию, или, если это удобнее, логарифм функции правдоподобия на экстремум и находим значение оценки, при которой функция достигает максимума. Эта оценка – оценка наибольшего правдоподобия.
Доверительный интервал – случайный интервал, в пределах которого с вероятностью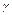 
находится неизвестный оцениваемый параметр. 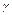- доверительная вероятность, или надёжность оценки.
1.Доверительный интервал для оценки мат ожидания СВ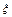 
.
< 
< + 
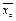
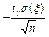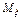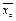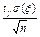, где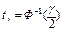 
2.Доверительный интервал для оценки среднеквадратического отклонения СВ .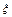
, где s –несмещённое выборочное среднеквадратичное отклонение, q – табличная функция, зависящая от объёма выборки n и надёжности оценки .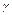
5. Понятие корреляционной зависимости. Теоретическая и эмпирическая линия регрессии.
Основные задачи теории корреляции – определение вида зависимости между случайными величинами и определение силы или тесноты этой зависимости.
Пусть в результате n испытаний (или в выборке объёма n) получены значения признаков X и Y.
Неупорядоченный статистический ряд значений случайных величин X и Y - таблица, первая строка которой – номер испытания, вторая – значение признака X, полученное в i-том испытании, третья – соответствующее значение признака Y.
Если некоторые пары значений признаков повторяются, ряд можно упорядочить и представить в виде корреляционной таблицы, то есть таблицы, содержащей матрицу частот nij, в которой результаты наблюдения обоих признаков записаны в порядке возрастания.
Корреляционная зависимость -
X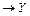 
- функциональная зависимость – взаимнооднозначная зависимость
Статистическая зависимость: любому значению признака X соответствует закон распределения соответствующих значений признака Y.
| yo | |||
| ni |
Корреляционная зависимость: частный случай статистической зависимости, при которой каждому значению одной случайной величины ставится в соответствие числовая характеристика соответствующего распределения другой.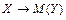 
или точнее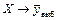 
Среднее арифметическое значение величины У, вычисленное при условии, что Х принимает фиксированное значение, называется условным средним и обозначается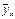 
. Аналогично, 
-условное среднее величины Х, при У = у.
Корреляционная зависимость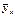 
от X:
| X | x1 | x2 | x3 | ….. | xn |
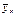
| yx1 | yx2 | yx3 | …… | yxn |
где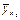 
, например = 
.
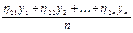Эмпирическая функция регрессии: ломаная, проведённая через точки с координатами (Xi;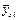 
)
Теоретическая линия регрессии:
По виду эмпирической линии регрессии, определим тип кривой (вид функции), которая наилучшим образом отразит зависимость между Х и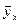 
. Если точки (
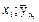) расположены «вдоль» прямой, строят «прямую регрессии», т.е. находят уравнение теоретической линии регрессии в виде
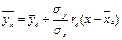
Аналогично строят регрессию икс на игрек.
6. Ковариация и корреляция случайных величин. Выборочный коэффициент корреляции.
Выборочный эмпирический корреляционный момент – величина, служащая для оценки тесноты связи между случайными величинами.
= 
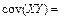
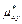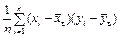. Если Х и У независимы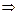 
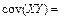0
При вычислении удобно пользоваться формулой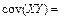 
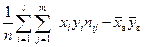
Размерность коэффициента корреляции равна произведению размерностей случайных величин Х и У.
Для получения безразмерной величины, разделим его на произведение средних квадратичных отклонений.
Выборочный коэффициент корреляции:
= 
= 
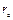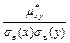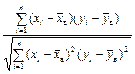или =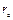 
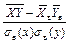
Свойства выборочного коэффициента корреляции.
1) Значения коэффициента корреляции изменяются на множестве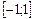 
. 
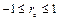, то есть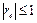 
2) Чем больше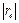 
, тем теснее связь между изучаемыми количественными признаками.
3) Если 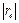=1 –связь между случайными величинами становится функциональной.
4) Если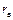 
=0 –корреляционная линейная зависимость между изучаемыми признаками отсутствует. Но это не исключает существования какого-либо другого вида корреляционной зависимости (например показательной).
7. Факторный анализ
Данные делятся на группы в зависимости от уровней (их p) влияющего на них фактора. Пусть в каждой группе q наблюдений значения фактора.
По каждой группе вычисляется средняя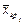 
.
Общая дисперсия показывает разброс всех данных относительно среднего значения.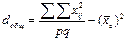 
; 
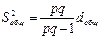
Факторная дисперсия показывает разброс средних групповых значений относительно общего среднего.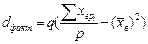 
; 
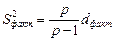
Остаточная дисперсия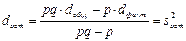 
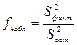
Отношение исправленной факторной к исправленной остаточной дисперсии является критерием, определяющим значимость влияния исследуемого фактора на измеряемый признак. Если наблюдаемое значение критерия превышает критическое, взятое из таблицы распределения Фишера – Снедекора, то гипотеза о влиянии фактора на измеряемый признак принимается.
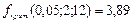
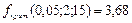
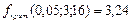
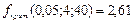
8. Статистические гипотезы – предположения о виде неизвестного распределения или о параметрах известных распределений.
Выдвигаемую гипотезу называют нулевой (основной) гипотезой. Обозначают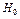 
.
Гипотезу, противоречащую основной называют конкурирующей или альтернативной -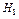 
Статистический критерий – случайная величина, служащая для проверки основной гипотезы.
Критическая область – область значений критерия, при которых гипотеза отвергается.
Область принятия гипотезы - область значений критерия, при которых гипотеза принимается.
В результате проверки гипотез могут совершаться ошибки первого и второго рода.
Ошибка первого рода – отвергается гипотеза 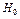, а она правильная - 
риск.
Ошибка второго рода – принимается гипотеза 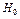, а она неправильная - 
риск.
, 
, 
, 
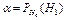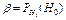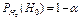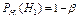
Алгоритм критерия согласия Пирсона: Выдвигается гипотеза о виде распределения неизвестной СВ, по данным выборки находим точечные оценки параметров распределения этой СВ методом моментов. Находим теоретические частоты, вычисляем значение критерия Пирсона и сравниваем его с критическим, взятым из тб. распред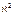 
, для заданных степеней свободы и уровня значимости.
Задачи проверки статистических гипотез:
1. О равенстве дисперсий
(распределение Фишера- Снедекора;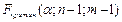 
)
Наблюдаемое значение критерия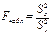 
2.О равенстве матожиданий
(распределние Стьюдента.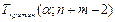 
)
При подтверждённой предыдущей гипотезе вычисляем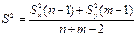 
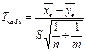
3. О равенстве матожидания заданному числу a при неизвестной дисперсии
(распределние Стьюдента; 
)
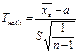
4. О равенстве матожидания заданному числу при известной дисперсии
(Функция Лапласа;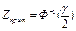 
)
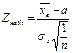
Вопросы к модулю по матстатистике.
1. Определение и задачи математической статистики.
2. Выборочный метод сбора статистических данных.
3. Статистическое распределение случайной величины. Эмпирическая функция распределения.
4. Полигон частот и гистограмма.
5. Выборочные характеристики.
6. Понятие точечных и интервальных оценок. Доверительный интервал.
7. Свойства точечных оценок.
8. Метод моментов и метод максимального правдоподобия для точечной оценки параметров распределения
9. Основные задачи и понятия теории корреляции
10. Ковариация и корреляция случайных величин. Выборочный коэффициент корреляции и его свойства
11. Эмпирическая и теоретическая линии регрессии.
12. Факторный анализ.
13. Статистические гипотезы. Алгоритм применения критерия согласия Пирсона.
14. Задачи проверки статистических гипотез.
Вопросы к экспресс опросу.
1) Чем занимается матстатистика?
2) Основные задачи матстатистики?
3) Что такое выборка и генеральная совокупность?
4) Какая выборка называется репрезентативной?
5) В чём суть повторны и бесповторных методов составления выборки?
6) В чём заключается типический и серийный способы составления выборки?
7) В чём заключается простой и механистический способы составления выборки?
8) Как выглядит статистическое распределение случайной величины?
9) Что такое накопленные частоты? Эмпирическаая фенкция распределения?
10) Как строят полигон частот и гистограмму?
11) Формула для вычисления среднего значения выборки
12) Формула для вычисления выборочной дисперсии
13) Формула для вычисления средневыборочного отклонения
14) Формула для вычисления начального эмпирического момента.
15) Формула для вычисления центрального эмпирического момента.
16) Понятие моды, медианы и размаха варьирования выборки
17) Формула для вычисления исправленной выборочной дисперсии.
18) Понятие точечной оценки и её точности.
19) Понятие несмещённой оценки.
20) Понятие эффективной оценки.
21) Понятие состоятельной оценки.
22) Метод моментов отыскания неизвестных параметров равномерного распределения исследуемого признака.
23) Метод моментов отыскания неизвестных параметров нормального распределения исследуемого признака.
24) Интервальная оценка. Доверительный интервал и надёжность оценки.
25) Формула для вычисления доверительного интервала для неизвестного матожидания нормальнораспределённой случайной величины.
26) Формула для вычисления доверительного интервала для неизвестного среднеквадратического отклонения нормальнораспределённой случайной величины.
27) Основные задачи теории корреляции.
28) Понятие корреляционной таблицы.
29) Понятие корреляционной зависимости.
30) Вид линий эмпирической и теоретической регрессии.
31) Формула для построения теоретической линии регрессии игрека на икс.
32) Формула для построения теоретической линии регрессии икса на игрек.
33) Расскажите о ковариации случайных величин.
34) Формула для вычисления коэффициента корреляции.
35) Свойства коэффициента корреляции.
36) Алгоритм применения факторного анализа.
37) Формула для вычисления факторных и общих дисперсий при равном количестве данных в каждой группе фактора.
38) Понятие статистических гипотез и критериев.
39) Статистические ошибки проверки гипотез.
40) Задача проверки гипотезы о равенстве двух дисперсий.
41) Задача проверки гипотезы о равенстве двух матожиданий.
42) Задача проверки гипотезы о равенстве матожидания заданному числу при известной дисперсии.
43) Задача проверки гипотезы о равенстве матожидания заданному числу при неизвестной дисперсии.
Date: 2015-06-08; view: 1107; Нарушение авторских прав