Выборочный метод сбора статистических данных

Модуль 6. Элементы математической статистики.

Вопрос 1. Определение и задачи математической статистики. Выборочный метод.

Математическая статистика – наука, занимающаяся разработкой методов сбора, регистрации и обработки результатов наблюдений (измерений) с целью познания закономерностей случайных массовых явлений. Результаты наблюдений (измерений) называются статистическими данными.

Если в теории вероятностей считается заданной модель явления и надо произвести расчёты возможного реального течения этого явления, то в мат. статистике исходят из каких-либо известных реализаций некоторых случайных событий (статистических данных), которые носят обычно числовой характер.

Мат. статистика разрабатывает методы, которые позволяют по этим статистическим данным подобрать подходящую теоретико- вероятностную модель.

Основные задачи математической статистики:

1) приближённое определение неизвестного закона распределения случайной величины;

2) приближённое определение неизвестных параметров распределения (их статистические оценки);

3) проверка правдоподобия гипотез о распределении случайной величины.

Выборочный метод сбора статистических данных.

Вся исследуемая совокупность однородных объектов называется генеральной совокупностью.

Множество из “n” объектов, отобранных случайным образом из генеральной совокупности, называется выборочной совокупностью - выборкой. Число “n” – объём выборки.

Выборочный метод - метод основанный на том, что по данным обследованиям выборки, выделенной из данной генеральной совокупности, делается заключение о всей генеральной совокупности.

Репрезентативная выборка – выборка, в которую каждый объект генеральной совокупности имеет одинаковую возможность попасть.

Если выборка репрезентативна, то результаты её изучения будут близки к результатам, которые могли бы быть получены, если бы исследовалась вся генеральная совокупность.

Способы составления выборки:

1) Повторный способ (серия независимых испытаний) – отобранный объект возвращается в генеральную совокупность.

2) Бесповторный способ – объект не возвращается в генеральную совокупность и получаем серию зависимых испытаний.

Различают: 1) простой – случайный способ составления выборки, когда генеральная совокупность не расчленяется; 2) механистический способ, когда ген. совокупность расчленяется на n групп и из каждой группы выбирают по 1 объекту; 3) типический способ – случайный выбор объектов из типической группы 4) серийный - совокупность делится на группы – серии и случайным образом выбирается одна целая группа.

Вопрос 2. Статистическое распределение случайной величины. Эмпирическая функция распределения. Полигон частот и гистограмма.

Пусть Х – случайная величина, количественное значение интересующего нас признака.

Составим простой статистический ряд:

N			…	n
X			…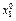

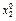
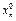
-– номер измерения количественного признака.

- значение признака, полученное в этом измерении.

Возможные различные значения случайной величины Х назовём вариантами. Составим новую таблицу, в первой строке которой расположим варианты в порядке возрастания, во второй строке – соответствующие числа 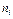- част о ты значений признака, показывающие, сколько раз наблюдалось i – тое значение признака. Эта таблица – статистическое распределение случайной величины Х – таблица значений признака, расположенных в порядке возрастания и соответствующих им частот.

Х				…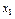
				…
				…
			+	…
				…

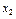
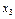
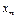
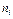
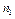
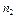
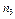
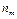
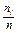
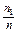
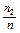
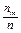
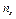
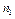
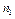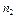
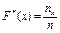
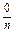
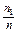
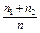
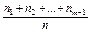
- вариационный ряд

- ряд частот значений признака

- ряд относительных частот

- ряд накопленных частот

- эмпирическая функция распределения выборки

Причём сумма частот признака равна объёму выборки n, а сумма относительных частот равна 1.

Накопленные частоты вычисляются по формуле 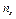= 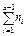, а эмпирическая функция распределения определяет относительную частоту события: «значение признака Х меньше заданного 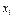». Эмпирическая функция распределения выборки – ступенчатая неубывающая функция. .

Если пары чисел 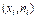определяют m точек плоскости, соединённых отрезками, то полученную ломаную линию назовём полигоном частот. Аналогично, по первой и третьей строке таблицы, строится полигон относительных частот.

Интервальное распределение частот – упорядоченная последовательность интервалов варьирования значений исследуемого признака с соответствующими частотами или относительными частотами попаданий в каждый из них значений исследуемого признака.

Число интервалов разбиения 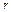определяется условиями проведения исследования, может быть вычислено по формулам 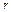= 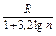или 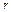= 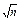. Для небольших выборок 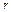обычно принимают равным числу от 6 до 15.

Откладывая на оси абсцисс полученные интервалы варьирования признака, а на оси ординат соответствующие им относительные частоты, делённые на ширину интервала (числа 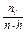, где 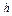- ширина интервала), получим гистограмму непрерывного признака. Кривая, «сглаживающая» гистограмму – эмпирическая функция плотности относительной частоты. Площадь соответствующей криволинейной трапеции равна 1.

Вопрос 3. Выборочные характеристики:

1) Выборочная средняя - 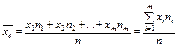- среднее значение признака.

2) Выборочная дисперсия 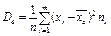или -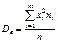

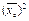
3) Средневыборочное отклоне ние 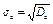- показатель разброса значений признака относительно его среднего значения.

4) Мода признака - 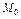– варианта, имеющая наибольшую частоту.

5) Медиана признака – 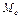- варианта признака, делящая вариационный ряд на две части, с равным числом вариант в каждой. Если число вариант чётно, медиана равна среднему значению для двух вариант середины ряда.

6) Размах варьирования – R - разность между максимальной и минимальной вариантой.

7) Начальный эмпирический момент порядка k: 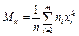. 8) 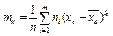- центральный эмпирический момент порядка k.

Date: 2015-06-08; view: 719; Нарушение авторских прав