
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Решение задачи. 1.Особенности задачи. Прежде всего, выясним, какие величины этой задачи могут быть вычислены уже известными методами
|
|
1.Особенности задачи. Прежде всего, выясним, какие величины этой задачи могут быть вычислены уже известными методами. Очевидно, что каждая из параллельных ветвей АВБ и АГБ (рис. 1) представляет собой неразветвлённую цепь с заданным напряжением на её зажимах
(точки А и Б). Поэтому
I1=U/Z1=U/ √r12+ ( L)2;
L)2;
I1= U/Z1=U/ √r12+ ( C)2.
C)2.
Иное положение с общим током L. Для его вычисления требуются новые методы. Поскольку общий ток / равен геометрической сумме токов ветвей I1 и I2, то возможен геометрический путь решения, основанный на применении векторной диаграммы. Существует и алгебраический путь решения (см. следующую задачу).
|
2_ Векторная диаграмма. Для неразветвлённых цепей, как было показано, удобно начинать построение векторной диаграммы с вектора тока, общего для всех участков цепи. Для цепи на
рис. 1 также желательно найти………………………………………………………………………………нет текста ……………
………………………………………
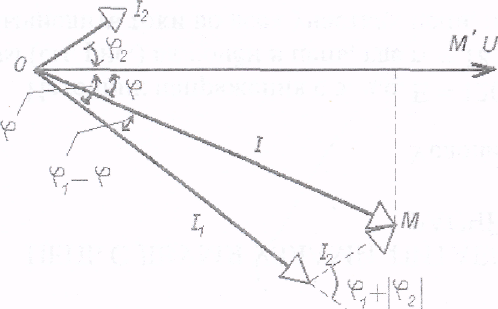
Рис 2 Векторная диаграмма для цепи из
двух параллельных ветвей по рис 1.
В ветви с активно-индуктивным сопротивлением ток I1 отстает по фазе на угол 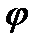 1 от напряжения U, а в ветви с активно-ёмкостным сопротивлением ток I2 опережает по фазе напряжение U на угол
1 от напряжения U, а в ветви с активно-ёмкостным сопротивлением ток I2 опережает по фазе напряжение U на угол 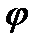 2. Общий ток I (рис 2) построен как геометрическая сумма токов I1, I2.
2. Общий ток I (рис 2) построен как геометрическая сумма токов I1, I2.
3, Вычисление токов. О токах ветвей уже говорилось выше. В нашем случае
I1= U/ √r12+ (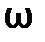 L)2=102/ √802+(3.14•0.19)2 =1.2 A
L)2=102/ √802+(3.14•0.19)2 =1.2 A
I2= U/ √r12+ (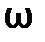 C)2=120/ √2602+(1/3.14•21.2•10-6)2=0.4 A
C)2=120/ √2602+(1/3.14•21.2•10-6)2=0.4 A
Эти токи смещены по фазе относительно напряжения на углы (без учета знака)
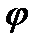 1=arcoc r1/z1=arcos 80/100=37o
1=arcoc r1/z1=arcos 80/100=37o
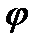 2 =arcos r2 / z2=arcos 260/300=30o
2 =arcos r2 / z2=arcos 260/300=30o
Общий ток I и его сдвиги по фазе 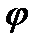 находим из треугольника токов ОКМ (рис. 2) по теореме косинусов:
находим из треугольника токов ОКМ (рис. 2) по теореме косинусов:
I=√I12+I22-2I1I2 cos OKM,
но
ОКМ=180о-(φ1+ φ2 )
а
cos[180o-(φ1+ φ2 )]=-cos(φ1+ φ2 ),
поэтому
I=√I12+I22-2I1I2 cos (φ1+ φ2 )=
=√1,22+0,42+2•1,2 • 0,4 • 0,39=1,4 А
По теореме синусов для треугольника ОКМ
I/ sin (φ1+ φ2 ) = I2/sin(φ1-φ)
откуда
sin(φ1-φ)=I1/ I=sin 67o=(0.4/1.4) • 0.92=0.264
или
φ=φ1-15о20’=21о 40’.
4, Вычисление мощностей. Активная мощность всей цепи
P=UI cos φ=120•1.4 cos22o=157o
Слагается из мощностей ветвей:
P1=I12 r1 = (1.2)2 • 80=115 Вт
P2=I22 r2= (0.4)2 • 260=42 Вт
(Действительно, Р1+Р2=115+42=157 Вт = Р)
Реактивная мощность всей цепи
Q=UI sin φ=120 • 1.4sin 22o= 62 вар
Равна алгебраической сумме реактивных мощностей ветвей:
Q1=UI1 sin φ1=120•1.2 •0,6= 86 вар
Q2=UI2 sin φ2=120 • 0,4(-0,5)= -24 вар
Где учтено, что полное сопротивление первой ветви имеет индуктивный характер (φ1>0), а второй ветви – емкостный (φ2<0);
Q=Q1+Q2=86-24=62 вар.
3,Расчет параллельного соединения активно – индуктивного и емкостного сопротивлений в цепи однофазного переменного тока.
1.Взять данные для своего варианта из таблицы в соответствии с № по списку в журнале.
2.Рассчитать неизвестные в таблице величины.
3.По результатам расчета построить векторную диаграмму
4.Рузультаты оформить на бланке отчета.
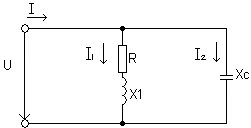
Таблица данных рис.1.
| № n\n | U B | I A | I1 A | I2 A | R Ом | L мГн | C мкФ | P Вт | Q вар | S ВА | Cos φ | fр Гц |
| 19,11 | 796,18 | |||||||||||
| 12,74 | 454,96 | |||||||||||
| 25,48 | 1592,36 | |||||||||||
| 9,55 | 636,94 | |||||||||||
| 19,11 | 530,79 |
Date: 2015-06-08; view: 423; Нарушение авторских прав