
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

ВВЕДЕНИЕ. Предлагается решить по 3 типовые задачи
Предлагается решить по 3 типовые задачи. Представлено 26 вариантов. Числовые данные вариантов приведены в таблицах. Последний (26-й вариант), каждой задачи решен, и, таким образом, даны примеры решения всех типовых задач.
При выполнении расчетно-графической работы студент должен сделать следующее:
1. Записать конкретное словесное условие задачи с числовыми значениями, взятыми из таблицы.
2. Записать краткое условие. Выразить числовые данные в единицах СИ.
3. Дать конкретный чертеж, поясняющий содержание задачи соответствующего варианта.
4. Решение сопроводить краткими, но исчерпывающими пояснениями, раскрывающими физический смысл употребляемых формул (указать основные законы, разъяснить буквенные обозначения величин).
5. Решить задачу в общем виде и получить рабочую формулу.
6. Подставить в рабочую формулу числовые значения, выраженные в единицах СИ.
7. Произвести вычисления искомых величин, руководствуясь правилами приближенных вычислений.
ЗАДАЧА 1. ПОЛЯРИЗОВАННЫЙ СВЕТ. ВРАЩЕНИЕ ПЛОСКОСТИ ПОЛЯРИЗАЦИИ СВЕТА
Варианты 1 – 26
Кристаллическая пластинка, обладающая оптической активностью с постоянной вращения α, помещена между двумя николями – поляризатором и анализатором (рис. 1а и 1б). На поляризатор падает естественный или линейно поляризованный (в зависимости от варианта) свет, интенсивность которого I0. После прохождения через поляризатор интенсивность света равна I1, а после прохождения через анализатор – I2. Угол между направлением колебаний светового вектора линейно поляризованной волны, подающей на поляризатор, и главной плоскостью поляризатора равен φ1, а угол между главными плоскостями анализатора и поляризатора равен φ2 (углы отсчитываются по часовой стрелке). Кристаллическая пластинка свет не поглощает, и толщина ее равна d. В николях теряется по 10 % проходящего через них света (неидеальные поляризатор и анализатор). Найти неизвестную величину, используя данные табл. 1. На рисунке по данным варианта показать углы φ1, φ2, φ3 и Δφ, где φ3 – угол поворота плоскости поляризации света в пластинке, Δφ – угол между 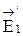 волны, падающей на анализатор, и главной плоскостью анализатора (см. рис. 1б).
волны, падающей на анализатор, и главной плоскостью анализатора (см. рис. 1б).
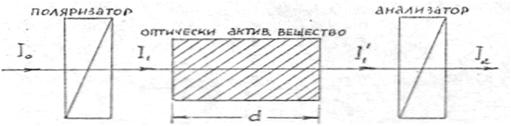 |
Рис. 1а. Прохождение света через систему поляризатор – вещество – анализатор (I 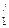 - интенсивность света на выходе из кристаллической
- интенсивность света на выходе из кристаллической
пластинки)
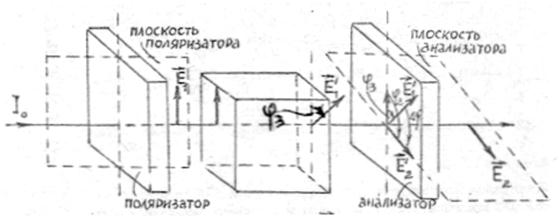 |
Рис. 1б. Направление колебаний
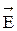 (состояние поляризации) световой волны при прохождении ее через систему
(состояние поляризации) световой волны при прохождении ее через систему
поляризатор – вещество – анализатор
Таблица 1
Данные для расчетов
| Вариант | I0 – естест. или линейно поляриз. | φ1, град | I1/I0 | φ2, град | I2/I0 | α, град/мм | d, мм |
| Естест. | - | ? | ? | - 30 | |||
| Линейно поляриз. | ? | ? | + 30 | ||||
| Линейно поляриз. | ? | ? | + 10 | ||||
| Продолжение таблицы 1 | |||||||
| Вариант | I0 – естест. или линейно поляриз. | φ1, град | I1/I0 | φ2, град | I2/I0 | α, град/мм | d, мм |
| Линейно поляриз. | ? | 0,5 | + 30 | ? | |||
| Естест. | - | ? | ? | 0,1 | - | ||
| Естест. | - | ? | 0,3 | + 10 | ? | ||
| Естест. | - | ? | 0,2 | ? | |||
| Линейно поляриз. | ? | ? | 0,11 | - 15 | 2,5 | ||
| Линейно поляриз. | ? | 0,8 | ? | ||||
| Линейно поляриз. | ? | ? | 0,05 | + 10 | 1,5 | ||
| Естест. | - | ? | 0,15 | - 10 | ? | ||
| Линейно поляриз. | ? | ? | 0,7 | - 20 | |||
| Естест. | - | ? | 0,4 | ? | |||
| Линейно поляриз. | ? | ? | 0,25 | + 20 | |||
| Естест. | - | ? | ? | + 25 | |||
| Естест. | - | ? | ? | 0,08 | + 30 | ||
| Естест. | - | ? | 0,35 | + 10 | ? | ||
| Линейно поляриз. | ? | ? | - 15 | 2,5 | |||
| Линейно поляриз. | ? | 0,01 | ? | 1,5 | |||
| Линейно поляриз. | ? | 0,7 | - 30 | ? | |||
| Линейно поляриз. | ? | ? | + 30 | ||||
| Линейно поляриз. | ? | ? | + 45 | ||||
| Линейно поляриз. | ? | ? | + 60 | ||||
| Естест. | - | ? | 0,3 | - 10 | ? | ||
| Естест. | - | ? | 0,3 | - 20 | ? | ||
| Естест. | - | ? | ? | + 30 | 1,5 |
Пример решения задачи № 1 (вариант № 26)
Дано: Решение:
|
естественный свет
φ2 = 900 (рис. 5в)
α = 30 град/мм
d = 1,5 мм
k = 10 % = 0,1

Найти: 1) I1/I0 -?
2) I2/I0 -?
2) Угол поворота плоскости поляризации линейно поляризованного света, прошедшего через оптически активное вещество, определяется по формуле 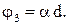
В нашем случае
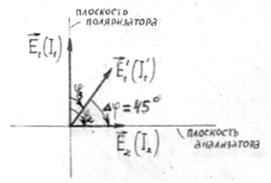
φ3 = 30 град/мм ∙ 1,5 мм = 450
Δφ = φ2 – φ3 = 900 – 450 = 450.
По закону Малюса для идеального анализатора
|
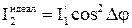 , а в данном случае
, а в данном случае
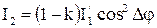 . Так как
. Так как 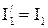 то
то
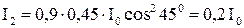 ;
;
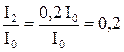 .
.
ЗАДАЧА 2. ИНТЕРФЕРЕНЦИЯ СВЕТА ОТ ДВУХ КОГЕРЕНТНЫХ
ИСТОЧНИКОВ
Варианты 1 – 26
Расстояние между двумя когерентными источниками света S1 и S2 равно d. Источники, испускающие монохроматический свет с длиной волны в вакууме λ0 = 0,5 мкм, расположены на расстоянии L от экрана. Рассмотреть два случая: 1) волны распространяются в однородной среде с абсолютным показателем преломления nср; 2) на пути первой волны помещена в ту же среду прозрачная пластинка (пленка) толщиной h с абсолютным показателем преломления n пл (рис. 2).
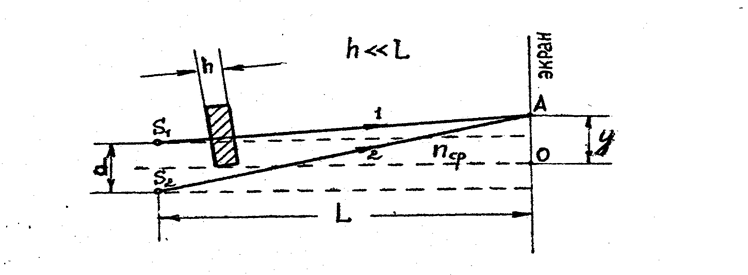
Определить для обоих случаев оптическую разность хода δ двух волн в зависимости от варианта или в точке О, одинаково удаленной от источников, или в точке А, расположенной на разных расстояниях от источников (табл. 2). Определить разность фаз Δφ двух интерферирующих волн в той же точке. Какая освещенность будет в этой точке – минимальная или максимальная? Нарисуйте конкретный чертеж, соответствующий Вашему варианту.
Рис. 2. Интерференция света от двух когерентных источников
(обычно у << L, d << L)
Таблица 2
Данные для расчетов
| Вариант | Точка на экране | d, м | у, м | L, м | h, мкм | ncp | nпл |
| А | 5 ∙ 10-4 | 2 ∙ 10-2 | 1,3 | 1,5 | |||
| О | - | - | 6,5 | 1,5 | 2,0 | ||
| А | 8 ∙ 10-4 | 4 ∙ 10-2 | 1,5 | 1,2 | |||
| О | - | - | 2,0 | 1,5 | |||
| А | 2 ∙ 10-4 | 5 ∙ 10-2 | 1,75 | 1,5 | |||
| О | - | - | 13,75 | 1,5 | 1,7 | ||
| А | 3 ∙ 10-4 | 1,6 ∙ 10-2 | 1,5 | 1,1 | 1,5 | ||
| О | - | - | 1,5 | 8,125 | 1,6 | 1,2 | |
| Окончание табл. 2 | |||||||
| Вариант | Точка на экране | d, м | у, м | L, м | h, мкм | ncp | nпл |
| А | 3,15 ∙ 10-4 | 1 ∙ 10-2 | 3,5 | 1,1 | 2,0 | ||
| О | - | - | 1,8 | 1,4 | |||
| А | 7 ∙ 10-4 | 1,5 ∙ 10-2 | 1,1 | 1,3 | |||
| О | - | - | 1,2 | 1,7 | |||
| А | 3,5 ∙ 10-4 | 0,05∙ 10-2 | 0,5 | 1,6 | 1,4 | ||
| О | - | - | 0,5 | 12,5 | 1,7 | 2,0 | |
| А | 6 ∙ 10-4 | 0,1 ∙ 10-2 | 1,5 | 7,3 | 1,5 | 2,0 | |
| О | - | - | 1,5 | 9,75 | 1,3 | 1,5 | |
| А | 4 ∙ 10-4 | 0,05 ∙ 10-2 | 0,8 | 1,9 | 1,4 | ||
| О | - | - | 0,8 | 22,5 | 1,4 | 1,5 | |
| А | 5 ∙ 10-4 | 0,3 ∙ 10-2 | 1,5 | 1,7 | 1,9 | ||
| О | - | - | 1,5 | 2,5 | 2,0 | 1,9 | |
| А | 1 ∙ 10-2 | 2 ∙ 10-4 | 1,1 | 1,3 | 1,5 | ||
| А | 2 ∙ 10-2 | 2 ∙ 10-4 | 1,2 | 1,5 | |||
| О | 3 ∙ 10-2 | 2 ∙ 10-4 | 1,3 | 1,3 | 2,0 | ||
| О | 4 ∙ 10-2 | 2 ∙ 10-4 | 1,4 | 1,5 | 1,8 | ||
| О | 5 ∙ 10-2 | 2 ∙ 10-4 | 1,5 | 2,0 | 1,3 | ||
| А | 9 ∙ 10-4 | 1 ∙ 10-2 | 10,5 | 1,5 |
Пример решения задачи № 2 (вариант 26)
Здесь и в последующих примерах приводится краткое условие задачи и ее краткое решение. Студентам во всех задачах следует записать полное словесное условие и давать подробное решение, как это сделано в примере решения предыдущей задачи № 1 (вариант 26).
|
Дано:
λ0 = 0,5 мкм = 0,5 ∙ 10-6 м
Рассматриваемая точка
на экране – точка А
d = 9 ∙ 10-4 м
у = 1 ∙ 10-2 м
L = 1 м
h = 10,5 мкм = 10,5 ∙ 10-6 м
ncp = 1
nпл = 1,5

Найти: 1) δ -?; 2) Δφ -?
L2 = ncp 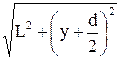 ;
;
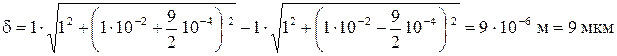 .
.
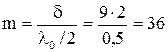 - четное число длин полуволн;
- четное число длин полуволн;
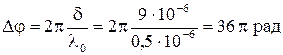 - четное число π.
- четное число π.
В точке А будет наблюдаться максимум освещенности.
2) Для случая 2 (с пластинкой):
δ = L2 – L1 = 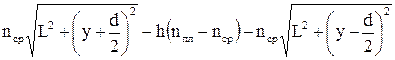 ;
;
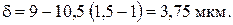
В точке А будет наблюдаться минимум освещенности, так как
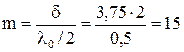 - нечетное число длин полуволн;
- нечетное число длин полуволн;
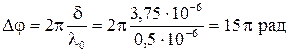 - нечетное число π.
- нечетное число π.
ЗАДАЧА 3. ДИФРАКЦИЯ СВЕТА НА ДИФРАКЦИОННОЙ
РЕШЕТКЕ (ДИФРАКЦИЯ ФРАУНГОФЕРА)
Варианты 1 – 26
На дифракционную решетку Д нормально падает монохроматический свет с длиной волны λ (фронт волны – плоский). На экране Э, расположенном за собирающей линзой параллельно решетке и отстоящем от нее на расстоянии L, наблюдается дифракционная картина (рис. 4). Расстояние между двумя дифракционными максимумами k-го и i-го порядков равно ℓ. Определить постоянную дифракционной решетки d, число n штрихов решетки на 1 мм ее длины и общее число N главных максимумов, получаемых с помощью этой решетки.
Нарисуйте конкретный чертеж, соответствующий Вашему варианту (табл. 4).
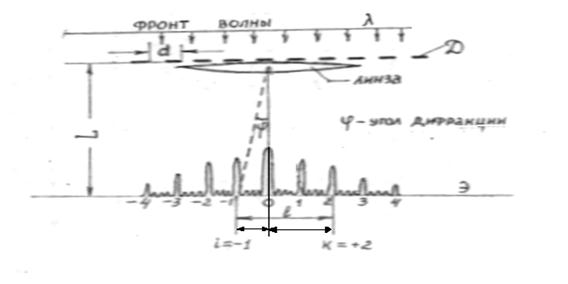 |
Рис. 4. Дифракция при прохождении света
через дифракционную решетку
Таблица 4
Данные для расчетов
| Вариант | λ, мкм | L, м | ℓ, см | k | i | d, мкм | n, 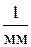
| N |
| 0,5 | + 1 | + 3 | ? | ? | ? | |||
| ? | 1,5 | - 1 | - 3 | ? | ? | |||
| Окончание табл. 4 | ||||||||
| Вариант | λ, мкм | L, м | ℓ, см | k | i | d, мкм | n, 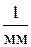
| N |
| 0,63 | ? | + 1 | + 2 | ? | ? | |||
| 1,15 | ? | - 1 | - 2 | ? | ? | |||
| 0,69 | ? | + 1 | ? | ? | ||||
| ? | 0,8 | - 1 | ? | ? | ||||
| 0,5 | 0,8 | ? | + 1 | - 2 | ? | ? | ||
| 0,63 | ? | + 1 | - 3 | ? | ? | |||
| 0,45 | ? | - 1 | + 2 | ? | ? | |||
| 0,38 | ? | - 2 | + 1 | ? | ? | |||
| ? | - 2 | + 3 | ? | ? | ||||
| ? | - 3 | + 3 | ? | ? | ||||
| 0,5 | ? | + 2 | ? | ? | ||||
| 0,5 | ? | + 1 | ? | ? | ||||
| ? | - 2 | ? | ? | |||||
| 1,15 | ? | + 3 | + 2 | ? | ? | |||
| ? | 0,5 | - 3 | - 2 | ? | ? | |||
| ? | 0,8 | + 3 | ? | ? | ||||
| ? | 1,5 | - 3 | ? | ? | ||||
| 1,15 | 1,5 | ? | - 3 | + 2 | ? | ? | ||
| ? | + 1 | ? | ? | |||||
| ? | 0,8 | - 1 | + 1 | ? | ? | |||
| 0,5 | ? | - 2 | + 2 | ? | ? | |||
| 0,6 | ? | - 1 | - 2 | ? | ? | |||
| 0,7 | ? | + 1 | + 2 | ? | ? | |||
| 0,65 | 0,5 | - 1 | + 2 | ? | ? | ? |
Пример решения задачи № 3 (вариант 26)
|
Дано:
λ = 0,65 мкм = 0,65 ∙ 10-6 м
L = 0,5 м
ℓ = 10 см = 0,1 м
k = - 1; i = + 2
 |
Найти: 1) d -?; 2) n -?; 3) N -?
|
Получаем: d tgφ1 = λ; d tgφ2 = 2λ или 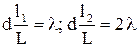 . Так как l1 = l – l2, получаем
. Так как l1 = l – l2, получаем 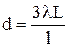 .
.
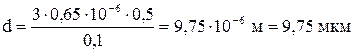 .
.
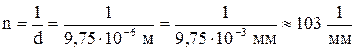 ;
;
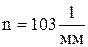 , то есть 103 штриха на 1 мм.
, то есть 103 штриха на 1 мм.
N = 2kmax + 1, где kmax получаем при φ = 900;
kmax = 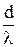 ; N =
; N = 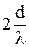 + 1 =
+ 1 = 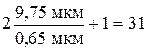 .
.
| <== предыдущая | | | следующая ==> |
| Критерии отбора | | |
Date: 2015-05-04; view: 688; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |
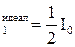 , а с учетом 10 % поглощения
, а с учетом 10 % поглощения
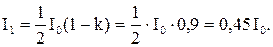
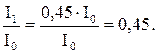
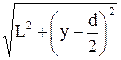 ;
L2 = ncp
;
L2 = ncp 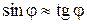 .
.