
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Примеры решения задач. Задача 1.Уравнение движения материальной точки имеет вид ,где .Определите среднее значение скорости
|
|
Задача 1. Уравнение движения материальной точки имеет вид 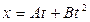 ,где
,где 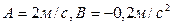 .Определите среднее значение скорости, и ускорения в интервале времени от 2 до 4 сек.
.Определите среднее значение скорости, и ускорения в интервале времени от 2 до 4 сек.
Решение: по определению средней скорости:
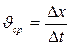

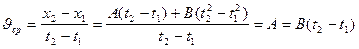
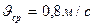
По определению среднего ускорения, оно равно:
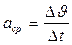 ,
, 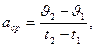
Мгновенная скорость может быть получена из уравнения
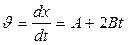 , тогда
, тогда 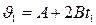 ,
, 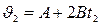 .
.
Подставляя эти выражения в уравнение для среднего ускорения, получим:
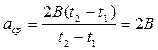 .
.
То есть ускорение точки при заданном законе движения постоянно, что с очевидностью получается из уравнения движения, поскольку ускорение (его мгновенное значение) может быть получено дифференцированием уравнения движения, что дает именно такой результат:
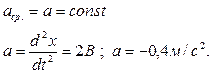
Ответ: 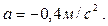
Задача 2. С какой высоты упало тело, если вторую половину своего пути оно пролетело за 1 сек?
Решение: Проиллюстрируем задачу графически.
Поскольку в условии задачи весь, участок движения разбит на два нам необходимо будет записать два уравнения движения.
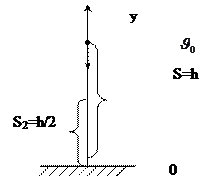 Так как на нижнем отрезке S2 пути движение происходило с неизвестной нам начальной скоростью, рационально записать уравнения движения для всего отрезка и верхнего его участка S1, поскольку в этих случаях начальная скорость равна нулю.
Так как на нижнем отрезке S2 пути движение происходило с неизвестной нам начальной скоростью, рационально записать уравнения движения для всего отрезка и верхнего его участка S1, поскольку в этих случаях начальная скорость равна нулю.
Учтем, что 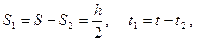 тогда
тогда 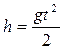 ,
, 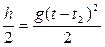 .
.
Решая эти уравнения совместно, подставляя верхнее уравнение в нижнее, получаем: 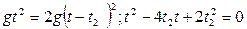
Решение этого уравнения имеет вид:
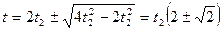
Второе решение квадратного уравнения не подходит по смыслу - все время движения не может быть меньше времени движения на втором участке пути.
Подставляя в выражение для h значение t, получаем:
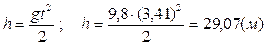 .
.
Ответ: h=29,07м.
Задача 3: Человек тянет груз за веревку, при этом веревка составляет с горизонталью угол 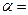 450, а коэффициент трения груза о горизонтальную поверхность, по которой он движется 0,01. Определите ускорение груза, если его масса 40 кг, а сила приложенная человеком к веревке 50 Н. Принять sin450=cos450 = 0,7.
450, а коэффициент трения груза о горизонтальную поверхность, по которой он движется 0,01. Определите ускорение груза, если его масса 40 кг, а сила приложенная человеком к веревке 50 Н. Принять sin450=cos450 = 0,7.
Решение: В данном случае необходим также рисунок, иллюстрирующий условия задачи. Выберем систему отсчета таким образом, чтобы ось OX совпадала с землей, а ось OY была к ней перпендикулярна. Груз будем считать достаточно малым, чтобы его можно принять за материальную точку.

Тогда на рисунке все силы будут приложены в одной точке – центре груза.
Кроме того, необходимо спроектировать, силу тяги на оси координат и найти ее компоненты 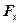 и
и 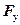 . Только после этого можно записать условие задачи в аналитической форме:
. Только после этого можно записать условие задачи в аналитической форме:
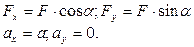
Составим систему уравнений описывающих движение тела. Основное уравнение движения в векторной форме будет иметь вид:
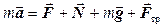
Для решения задачи его надо записать в скалярной форме в проекциях на оси OX и OY, то есть оно распадается на два скалярных уравнения:
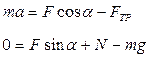
Кроме того, следует учесть зависимость силы трения скольжения от N. Окончательно система уравнений имеет вид:
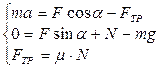
Выразив из двух последних уравнений N и F ТР, подставим их в первое и получим окончательно:
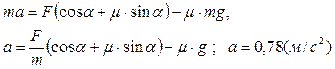
Ответ: а=0,78 м/с2.
Задача 4. К шару массой 2кг и радиусом 10см прикреплен стержень массой 4,8кг и длиной 1,2м, являющийся продолжением диаметра шара. Найти момент инерции системы относительно оси, проходящей через свободный конец стержня перпендикулярно к нему.
 |
Решение. Момент инерции шара относительно оси О2О2 проходящей через центр шара 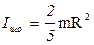 .
.
Момент инерции шара относительно ОО по теореме Штейнера равен:
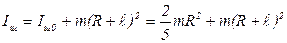
Момент инерции стержня относительно оси О1О1:
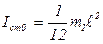
Момент инерции стержня относительно оси ОО по теореме Штейнера:
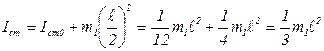
Суммарный момент инерции относительно оси ОО:
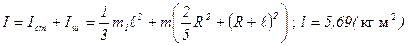
Ответ: 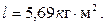
Задача 5. Блок имеет неподвижную ось вращения. Масса блока 1кг, радиус равен 0,2м. На блок намотана нить, к концу которой привязан груз массой 2кг. С каким ускорением будет двигаться груз?
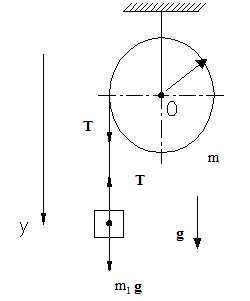 |
Решение. Груз движется поступательно, IIзакон Ньютона для него имеет вид:
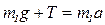
В проекции на ось у получим:
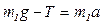 (1)
(1)
Блок вращается равноускоренно, для него запишем основное уравнение динамики вращательного движения:
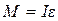 (2), где
(2), где 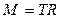 (3)
(3)
Для однородного диска
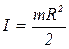 (4)
(4)
Угловое ускорение связано с тангенциальным ускорением соотношением:
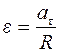 (5)
(5)
Подставив выражения 3, 4, 5 в уравнение (2), получим:
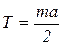 (6)
(6)
Решая совместно (1) и (6), получаем:
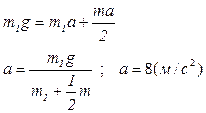
Ответ: а=8м/с2.
Задача 6. Человек массой 60кг стоит на краю платформы, имеющей форму диска радиусом 1м. Момент инерции платформы 20кг·м2. Платформа вместе с человеком вращается с угловой скоростью 1рад/с. Какую работу совершит человек, перейдя в центр диска? Момент инерции человека считать, как для материальной точки.
Решение. Поскольку взаимодействие происходит между человеком и платформой, систему считаем замкнутой и применяем закон сохранения момента импульса. В начальный момент времени момент инерции системы: 
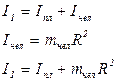
Момент импульса системы:
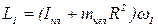
Когда человек перешел в центр платформы, его момент инерции стал равен 0, угловая скорость изменилась до ω2, а момент импульса
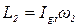
По закону сохранения момента импульса:
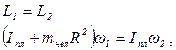
откуда
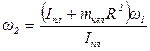
Начальная кинетическая энергия системы
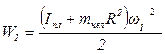
Человек, перейдя в центр диска, совершил работу, что привело к изменению кинетической энергии системы, кинетическая энергия стала равной W2.
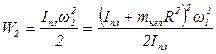
По закону сохранения энергии работа равна:
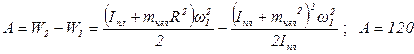 (Дж)
(Дж)
Ответ: А=120 Дж.
Задача 7. В сосуде объемом 2м3 находится смесь 4кг гелия и 2кг водорода при температуре 27С. определить давление и молярную массу смеси газов.
Решение. Воспользуемся уравнением Клайперона – Менделеева, применив его к гелию и водороду:
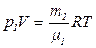 (1)
(1)
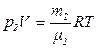 (2)
(2) 
где р1 – парциальное давление гелия; m1 – масса гелия; 
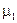 - его молярная масса; V - объем сосуда; Т - температура газа; R =8,31 Дж/(моль • К) - молярная газовая постоянная; p2 - парциальное давление водорода; m2 - масса водорода;
- его молярная масса; V - объем сосуда; Т - температура газа; R =8,31 Дж/(моль • К) - молярная газовая постоянная; p2 - парциальное давление водорода; m2 - масса водорода; 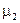 - его молярная масса. Под парциальным давлением p1 и р2 понимается то давление, которое производил бы газ, если бы он только один находился в сосуде. По закону Дальтона давление смеси равно сумме парциальных давлений газов, входящих в состав смеси:
- его молярная масса. Под парциальным давлением p1 и р2 понимается то давление, которое производил бы газ, если бы он только один находился в сосуде. По закону Дальтона давление смеси равно сумме парциальных давлений газов, входящих в состав смеси:
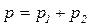 (3)
(3)
Из уравнения (1) и (2) выразим p1 и р2 подставим в уравнение (3).
Имеем
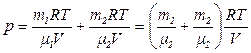 (4)
(4)
Date: 2015-05-04; view: 833; Нарушение авторских прав