
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Измерения и обработка результатов измерений
|
|
3.1. Упражнение 1. Определение коэффициента жесткости пружин.
3.1.1. С помощью динамометра измерить веса входящих в комплект лабораторного стенда грузов (имеющих форму цилиндра, параллелепипеда и шара). Полученные результаты взвешиваний записать в колонку 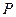 таблицы 1.
таблицы 1.
3.1.2. К каждой из имеющихся на стенде пружин подвесить в следующем порядке тела:
| - тело в форме параллелепипеда; | |
| - тела в форме параллелепипеда и цилиндра; | |
| - тело в форме шара. |
С помощью измерительной линейки на подставке 4 (см. рис.4) измерить положения точки подвеса тел к пружине. Результаты измерений записать в колонку 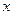 таблицы 1. Т.к. положение нижнего конца ненагруженной пружины (при данной методике измерений) является трудно определимой величиной, то опытное определение коэффициента жесткости пружины
таблицы 1. Т.к. положение нижнего конца ненагруженной пружины (при данной методике измерений) является трудно определимой величиной, то опытное определение коэффициента жесткости пружины 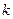 сделаем следующим образом. Пусть положение нижнего конца свободной пружины есть
сделаем следующим образом. Пусть положение нижнего конца свободной пружины есть 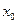 , а при подвешивании к пружине груза весом
, а при подвешивании к пружине груза весом 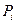 оно составит
оно составит 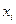 . Тогда формулу (2.2) запишем в виде
. Тогда формулу (2.2) запишем в виде
 , , 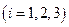 . .
| (2.3) |
Так как при трех измерениях для различных грузов и одной пружины величины 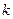 и
и 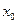 являются неизменными, то из уравнений (2.3) можно определить коэффициент жесткости пружины, исключив неизвестную величину
являются неизменными, то из уравнений (2.3) можно определить коэффициент жесткости пружины, исключив неизвестную величину 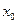 следующим образом:
следующим образом:
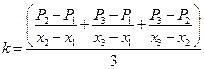
| (2.4) |
Результаты вычислений величины 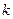 для каждой пружины занести в таблицу 1 в соответствующую колонку.
для каждой пружины занести в таблицу 1 в соответствующую колонку.
3.1.3. Определить зависимость периода собственных колебаний пружинных маятников от массы груза. Для этого измерить секундомером время  полных
полных  колебаний маятника, а период
колебаний маятника, а период 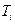 собственных колебаний определить по формуле
собственных колебаний определить по формуле
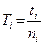
| (2.5) |
для каждой из пружин при различных грузах (таких же как и в п. 3.1.2), имеющих массы 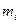 . Построить график зависимости
. Построить график зависимости  от
от 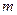 (по оси абсцисс откладывают массу
(по оси абсцисс откладывают массу 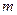 ).
).
3.1.4. Найти зависимость собственных колебаний пружинного маятника от коэффициента жесткости пружин 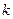 . Для этого взять из таблицы 1 значения периода
. Для этого взять из таблицы 1 значения периода  собственных колебаний маятников с различными пружинами, нагруженных одним и тем же грузом
собственных колебаний маятников с различными пружинами, нагруженных одним и тем же грузом 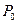 , а затем построить график зависимости
, а затем построить график зависимости 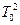 от величины, обратно пропорциональной
от величины, обратно пропорциональной 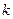 (по оси абсцисс откладывают значения
(по оси абсцисс откладывают значения 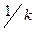 ).
).
3.1.5. По формуле
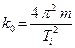
| (2.6) |
вычислить теоретический коэффициент жесткости пружин, используя полученные ранее (см. п. 3.1.3) опытным путем значения 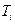 . Сравнить вычисленные значения
. Сравнить вычисленные значения 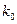 с результатами вычислений, проведенными по формуле (2.4) для одних и тех же пружин. Результаты анализа привести в выводах к отчету.
с результатами вычислений, проведенными по формуле (2.4) для одних и тех же пружин. Результаты анализа привести в выводах к отчету.
Таблица 1.
| №№ опыта | 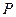 ,
Н ,
Н
| 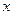 ,
см ,
см
| 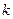 ,
Н/м ,
Н/м
|  ,
с ,
с
| 
| 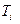 ,
с ,
с
| 
| 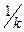
| 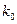
|
| I. | Первая пружина | ||||||||
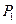 . .
| 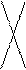
| 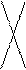
| |||||||
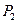 . .
| |||||||||
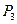 . .
| |||||||||
| Средние значения | 
| 
| |||||||
| II. | Вторая пружина | ||||||||
 . .
| 
| 
| |||||||
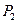 . .
| |||||||||
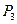 . .
| |||||||||
| Средние значения | 
| 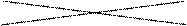
| |||||||
| III. | Третья пружина | ||||||||
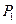 . .
| 
| 
| |||||||
 . .
| |||||||||
 . .
| |||||||||
| Средние значения | 
| 
|
3.1.5. Сделать вывод, проведя анализ полученных результатов.
3.2. Упражнение 2. Определение логарифмического декремента затухания пружинного маятника методом сравнения амплитуд.
3.2.1 Грузов в виде шара с помощью соединительной проволоки подвесить к пружине с наименьшим 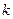 , а затем поместить в сосуд с жидкостью и привести маятник в колебание (соединительная проволока используется для того, чтобы затухания колебаний не вызывались движением пружины в жидкости, а сила упругости при подвешивании груза практически бы не изменялась). Измерить время
, а затем поместить в сосуд с жидкостью и привести маятник в колебание (соединительная проволока используется для того, чтобы затухания колебаний не вызывались движением пружины в жидкости, а сила упругости при подвешивании груза практически бы не изменялась). Измерить время 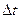 , за которое начальная амплитуда
, за которое начальная амплитуда 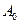 уменьшится в
уменьшится в 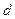 раз (т.е.
раз (т.е. 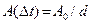 ). Первоначальную амплитуду установить при помощи отклонения груза в интервале от 25 до 40 мм. Значение
). Первоначальную амплитуду установить при помощи отклонения груза в интервале от 25 до 40 мм. Значение 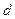 задает преподаватель (в противном случае брать
задает преподаватель (в противном случае брать 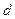 =2).
=2).
3.2.2 Вычислить логарифмический декремент затухания 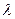 . Для этого формулу (1.8) следует преобразовать следующим образом. Поскольку время уменьшения амплитуды колебаний составляет
. Для этого формулу (1.8) следует преобразовать следующим образом. Поскольку время уменьшения амплитуды колебаний составляет 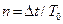 периодов колебаний, то отношение амплитуд
периодов колебаний, то отношение амплитуд
 . .
|
Отсюда после логарифмирования
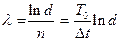
| (2.7) |
По этой формуле вычислить 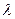 не менее трех раз. Для этого пункт 3.2.1. данного упражнения необходимо выполнить трижды, каждый раз задав отличное от предыдущих значение начальной амплитуды колебаний груза. При определении
не менее трех раз. Для этого пункт 3.2.1. данного упражнения необходимо выполнить трижды, каждый раз задав отличное от предыдущих значение начальной амплитуды колебаний груза. При определении 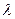 считать, что период
считать, что период  затухающих колебаний равен периоду
затухающих колебаний равен периоду 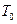 свободных колебаний маятника.
свободных колебаний маятника.
3.2.3 По формуле (1.10) найти значение коэффициента сопротивления для каждого значения амплитуды.
3.2.4 Найти среднее значение и доверительный интервал коэффициента сопротивления как для прямых измерений.
Результаты измерений и вычислений записать в таблицу 2.
Таблица 2.
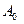
|  ,
с ,
с
| 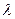
| 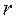 , кг/с , кг/с
| 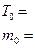
| |
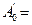
| 
| 
| |||
| 2. | |||||
| 3. | |||||
| Средние значения | |||||
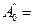
| 1. | 
| 
| ||
| 2. | |||||
| 3. | |||||
| Средние значения | |||||
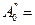
| 1. | 
| 
| ||
| 2. | |||||
| 3. | |||||
| Средние значения |
Контрольные вопросы:
- Объясните методику определения коэффициента жесткости.
- Объясните методику определения логарифмического декремента затухания пружинного маятника.
- Дайте определение колебательного процесса физической системы.
- Дайте определение амплитуды колебания.
- Дайте определение фазы колебаний. На сколько изменяется фаза за время одного полного колебания?
- Какие колебания называются гармоническими?
- Какие колебания называются свободными?
- Запишите дифференциальное уравнение свободных колебаний с одной степенью свободы и его решение.
- Что такое степень свободы? Сколькими степенями свободы может обладать пружинный маятник, изображенный на рис. 2в?
- Что называется квазиупругой силой? Возвращающей силой?
- Что такое затухающие колебания?
- Запишите дифференциальное уравнение затухающих колебаний и его решение.
- Какие из механических систем называются диссипативными?
- Раскройте физический смысл декремента затухания.
ЛИТЕРАТУРА:
1. Савельев И.В. Курс общей физики, т.1.-М.:"Наука",-1987.-320с..
2. Детлаф А.Л., Яворский Б.М. Курс физики, т.1.-М.:"Высш.шк."
3. Трофимова Т.И. Курс физики.- М.:"Высш.шк.",-1990.-478с.
Date: 2015-05-04; view: 587; Нарушение авторских прав