
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Краткие теоретические сведения. Колебательным движением называется движение, обладающее той или иной степенью повторяемости во времени
|
|
Колебательным движением называется движение, обладающее той или иной степенью повторяемости во времени. Движение называется периодическим, если значения величин, изменяющихся в процессе движения. Повторяются через равные промежутки времени.
Систему, совершающую колебания, независимо от ее природы называют осциллятором.
1.1. Свободные колебания. Для тела (точки), совершающей колебания, существует положение устойчивого равновесия. Вывести тело из этого состояния можно, приложив внешнюю силу. Тело, выведенное из состояния равновесия и представленное самому себе, совершает колебания около положения равновесия. Такие колебания называются собственными или свободными. Частота 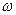 , с которой система совершает такие колебания, называется собственной.
, с которой система совершает такие колебания, называется собственной.
Простейшим типом колебаний являются гармонические, т.е. такие колебания, при которых колеблющаяся величина изменяется со временем по закону синуса или косинуса.
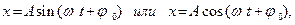
|
где 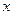 - колеблющаяся величина (смещение, скорость, ускорение, сила и т.п.),
- колеблющаяся величина (смещение, скорость, ускорение, сила и т.п.), 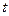 - время,
- время, 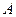 - амплитуда колебания (амплитуда равна максимальному абсолютному значению отклонения колеблющейся величины от положения равновесия),
- амплитуда колебания (амплитуда равна максимальному абсолютному значению отклонения колеблющейся величины от положения равновесия), 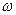 - циклическая или круговая частота.
- циклическая или круговая частота.
Физический смысл циклической частоты состоит в том, что она численно равна числу колебаний, совершаемых за 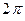 секунд, т.е.
секунд, т.е.

|
где 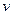 - частота колебаний, т.е. число колебаний, совершаемых за единицу времени,
- частота колебаний, т.е. число колебаний, совершаемых за единицу времени,  - период колебаний – время, за которое совершается одно полное колебание.
- период колебаний – время, за которое совершается одно полное колебание.
Величина 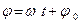 называется фазой колебания. Фаза колебания – функция времени, которая определяет значение колеблющейся величины
называется фазой колебания. Фаза колебания – функция времени, которая определяет значение колеблющейся величины 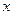 в данный момент времени
в данный момент времени 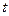 . Она показывает, какую часть от амплитуды
. Она показывает, какую часть от амплитуды 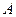 составляет смещение в данный момент времени:
составляет смещение в данный момент времени: 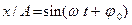 . Величина
. Величина 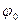 называется начальной фазой колебания. Она определяет значение величины
называется начальной фазой колебания. Она определяет значение величины 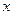 в начальный момент времени
в начальный момент времени 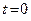 .
.
|
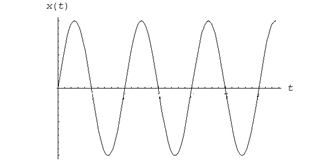
| Рис. 1. |
График гармонических колебаний изображен на рис. 1.
Дифференциальное уравнение гармонических колебаний с одной степенью свободы (см. рис. 2.а) имеет вид
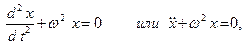
|
где 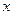 - смещение колеблющейся системы.
- смещение колеблющейся системы.
Если в уравнение (1.2) подставить одно из решений (1.1), то получим
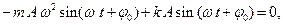
|
| а) | 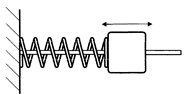
| откуда
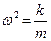 Если система может совершать два независимых друг от друга колебания в двух взаимно перпендикулярных направлениях, то такая система обладает двумя степенями свободы (рис. 2 б).
Если система совершает колебания около положения равновесия (после того как она каким-либо образом была выведена из положения устойчивого равновесия) без воздействия переменных внешних сил., то такие колебания называются собственными или свободными
Частота, с которой система совершает такие колебания, называется собственной частотой системы.
Если система может совершать два независимых друг от друга колебания в двух взаимно перпендикулярных направлениях, то такая система обладает двумя степенями свободы (рис. 2 б).
Если система совершает колебания около положения равновесия (после того как она каким-либо образом была выведена из положения устойчивого равновесия) без воздействия переменных внешних сил., то такие колебания называются собственными или свободными
Частота, с которой система совершает такие колебания, называется собственной частотой системы.
|
| б) | 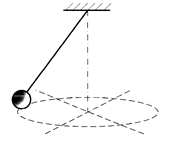
| |
| с) | 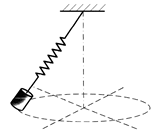
| |
| Рис. 2. |
1.2. Пружинный маятник. Примером гармонического осциллятора является пружинный маятник. Пружинный маятник – это груз массой т, закрепленный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой или квазиупругой силы 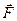 (силы, имеющие иную природу, чем упругие силы, но также удовлетворяющие уравнению
(силы, имеющие иную природу, чем упругие силы, но также удовлетворяющие уравнению 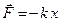 , называются квазиупругими). Эта сила всегда направлена к положению равновесия, а смещение
, называются квазиупругими). Эта сила всегда направлена к положению равновесия, а смещение 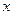 - в противоположную сторону, поэтому значения силы и смещения имеют противоположные знаки. Такая сила называется возвращающей силой. По второму закону Ньютона для возвращающей силы имеем
- в противоположную сторону, поэтому значения силы и смещения имеют противоположные знаки. Такая сила называется возвращающей силой. По второму закону Ньютона для возвращающей силы имеем
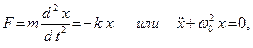
|
где 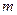 - масса груза,
- масса груза, 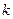 - коэффициент упругости пружины,
- коэффициент упругости пружины,
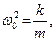
|
где  - циклическая частота,
- циклическая частота, 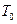 - период собственных колебаний.
- период собственных колебаний.
Из формулы (1.5) легко определить период собственных упругих колебаний груза на пружине. Так как
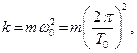
|
то

|
1.3. Затухающие колебания. Если колеблющаяся система находится в вязкой среде, то колебания через некоторое время прекратятся. Это явление представляет собой затухающее колебание.
Затухающими колебаниями называются колебания, энергия которых уменьшается с течением времени. В результате амплитуда колебаний уменьшается и колебания затухают.
Система тел, механическая энергия которых постепенно уменьшается за счет преобразования в другие виды энергии, называется диссипативной. Все реальные колебательные системы являются диссипативными. Энергия в диссипативной системе расходуется на работу против сил трения. Затухающие колебания совершаются при действии двух сил: упругой силы 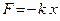 и силы сопротивления
и силы сопротивления 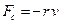 среды. Уравнение затухающего колебания при небольших затуханиях имеет вид:
среды. Уравнение затухающего колебания при небольших затуханиях имеет вид:
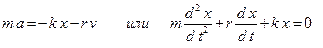 , ,
|
или
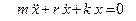 , ,
|
где 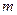 - масса колеблющегося тела,
- масса колеблющегося тела, 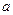 -ускорение тела,
-ускорение тела, 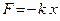 - величина возвращающей силы,
- величина возвращающей силы, 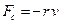 -сила сопротивления среды,
-сила сопротивления среды, 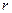 - коэффициент сопротивления среды,
- коэффициент сопротивления среды, 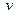 - скорость движения тела в среде. Решение уравнения (1.7) дает зависимость смещения
- скорость движения тела в среде. Решение уравнения (1.7) дает зависимость смещения 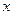 от времени
от времени 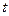 :
:
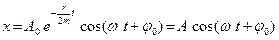
|
где 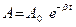 - амплитуда затухающих колебаний,
- амплитуда затухающих колебаний, 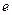 - основание натурального логарифма,
- основание натурального логарифма, 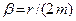 - коэффициент затухания,
- коэффициент затухания, 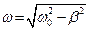 - циклическая частота затухающих колебаний системы,
- циклическая частота затухающих колебаний системы, 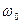 - собственная циклическая частота свободных колебаний системы (колебаний системы вне вязкой среды).
- собственная циклическая частота свободных колебаний системы (колебаний системы вне вязкой среды).
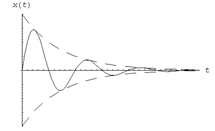 Рис. 3. Рис. 3.
| График затухающих колебаний при 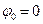 показан на рис. 3.
Отношение двух последующих амплитуд одного и того же знака показан на рис. 3.
Отношение двух последующих амплитуд одного и того же знака  и и 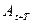 , отстоящих друг от друга на период равно , отстоящих друг от друга на период равно
| |
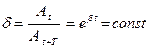
| ||
и называется декрементом затухания. Натуральный логарифм от этого отношения
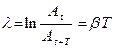
|
называется логарифмическим декрементом затухания.
В случае небольших затуханий 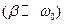 можно считать, что
можно считать, что 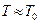 . Тогда
. Тогда
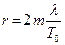
|
Date: 2015-05-04; view: 1008; Нарушение авторских прав