
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Методы расчета конструкций
|
|
Метод расчета фундаментов зависит от формы подошвы и относительной гибкости фундамента. Если конструкция имеет удлиненную прямоугольную опорную площадь, причем любая полоса шириной 1 м, выделенная в поперечном направлении из конструкции, работает в одинаковых условиях со всякой другой подобной полосой, т.е. имеет одинаковую жесткость и одинаковое распределение внешней нагрузки (рис.35), то расчет этой полосы проводится в условиях плоской задачи. При этом длина опорной площади должна быть по крайней мере в 3 раза больше ширины. В условиях плоской задачи рассчитываются главным образом фундаменты гидротехнических сооружений.

Рис.35. Схема выделения полосы из конструкции для расчета в условиях плоской задачи
Круглые и кольцевые фундаментные плиты рассчитываются на основе решения осесимметричной задачи. К ним относятся фундаменты доменных печей, фундаменты типа конусных оболочек и т.п.
Ленточные фундаменты под колонны рассчитываются как балки в условиях пространственной задачи. Фундаменты из перекрестных лент в силу сложности их конструкции рассчитываются по гипотезе Винклера. Плоские прямоугольные фундаменты под отдельные колонны рассчитываются как прямоугольные плиты в условиях пространственной задачи. При значительной их жесткости допустимо проводить расчет обычным способом, исходя из гипотезы о равномерном распределении реактивных давлений. Сплошные фундаментные плиты под ряды колонн или под стены (в том числе каркасных зданий), под полы промышленных зданий и т.п. рассчитываются с помощью ЭВМ как плиты большой протяженности.
Методы расчета конструкций на упругом основании (кроме плит большой протяженности) разделяются на две группы:
методы, в которых на основе условий равновесия и условия полного примыкания подошвы балки или плиты к грунту составляются одна или две системы линейных уравнений с несколькими неизвестными; решение этих систем позволяет определить эпюру реактивных давлений, а затем уже и эпюры изгибающих моментов, поперечных сил и прогибов (осадок);
методы, основанные на использовании готовых таблиц всех этих расчетных величин; такие таблицы составлены для большинства типов конструкций при различной их относительной гибкости, характере и размещении нагрузок и значительно сокращают время и труд расчетчика.
И в том, и в другом случае трением между подошвой фундамента и основанием принято пренебрегать (в запас прочности).
Основными методами, требующими решения систем уравнений, являются следующие:
1. Метод Б. Н. Жемочкина. Этот метод применим для расчета как балок в условиях пространственной задачи, так и полос в условиях плоской задачи. Здесь вся опорная площадь фундамента разбивается на ряд участков, причем в пределах каждого участка реакции грунта для упрощения считаются равномерно распределенными (рис.36).
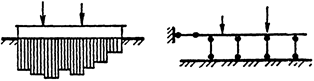
Рис.36. К расчету балки или полосы по методу Б.Н.Жемочкина
Между балкой (полосой) и основанием в середине каждого участка помещается абсолютно жесткий стержень (на рис.36 для ясности число стержней сокращено). Горизонтальный стержень поставлен для того, чтобы сделать систему неизменяемой: он никакой роли в расчете не играет. Постановкой вертикальных стержней-связей ставится условие, что вертикальные перемещения балки и основания в местах этих стержней одинаковы.
Неизвестными в расчете являются силы Fi в стержнях, осадка si и угол поворота tg αi в каком-либо сечении балки, принимаемом за начальное. Эти неизвестные определяются исходя из условия равенства прогибов балки и осадки грунта в точках, где поставлены стержни. К полученным контактным уравнениям прибавляются два уравнения, вытекающие из условия равновесия.
Аналогичный метод тем же автором предложен для расчета круглых и кольцевых плит.
Метод Б. Н. Жемочкина особенно удобен при переменном сечении балки или сложной форме подошвы. Он обобщается на случай, когда основание представляет собой сжимаемый слой конечной толщины. Метод неприменим для расчета прямоугольных плит в строгой постановке, когда в каждой точке плиты определяются два момента, изгибающих плиту соответственно в продольном и поперечном направлениях. Его нельзя также использовать для расчета длинных ленточных фундаментов под ряд колонн.
2. Метод М. И. Горбунова-Посадова. Этот метод охватывает все основные типы конструкций на упругом основании. Эпюра реактивных давлений здесь определяется в виде многочлена 10-й степени. При симметрично нагруженной полосе многочлен для плоской задачи имеет вид:
р (х) = а 0 + а 2 х 2 + а 4 х 4 + а 6 х 6 + а 8 х 8 + а 10 х 10, (136)
где х=х`/l – приведенное расстояние от середины полосы до данной точки (где х ` - действительное расстояние; l – полудлина полосы).
При нессиметричной нагрузке к многочлену (136) добавляется многочлен с нечетными степенями х 9-й степени. Расчет при симметричной нагрузке приводит к решению системы из шести уравнений относительно неизвестных а2i, а в общем случае – двух систем с шестью и пятью неизвестными. Эти системы получаются путем приравнивания перемещений поверхности грунта ω (х) от давлений р (х) прогибам полосы от тех же давлений. Давления р (х) для полосы являются реактивными давлениями, направленными снизу вверх. И перемещения поверхности, и прогибы выражаются так же через степенные ряды, коэффициенты которых линейно зависят от коэффициентов а2i и а2i+1. Приравнивание коэффициентов при одинаковых степенях в уравнении перемещений и прогибов и дает нужные системы уравнений. При пространственной задаче метод аналогичен, но в решении участвуют уже двойные степенные ряды.
Расчет конструкций на упругом основании по таблицам
Расчет балок и плит на упругом основании по гипотезе упругого полупространства или сжимаемого слоя по таблицам готовых расчетных величин дан в виде основных сведений по классификации балок и плит для выбора нужных таблиц, а также таблицы для наиболее важных случаев расчета.
Расчет балок (полос) в условиях плоской задачи. В таблицах даны реактивные давления, поперечные силы и изгибающие моменты для полос, принимаемых за абсолютно жесткие, для полос конечной длины и жесткости, бесконечных и полубесконечных. Предусмотрены случаи равномерной нагрузки и нагрузки в виде сосредоточенной силы или момента, приложенных в любом сечении.
Полоса считается абсолютно жесткой, если показатель ее гибкости t (величина безразмерная) удовлетворяет неравенству
t = 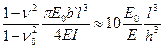 < 1, (137)
< 1, (137)
где Е 0 и ν 0 – модуль деформации и коэффициент Пуассона грунта; Е и ν – модуль упругости и коэффициент Пуассона материала полосы; I – момент инерции сечения полосы; l – полудлина полосы; h – высота; b` - ширина, равная 1 м.
Второе приближенное значение для t в формуле (137) относится к полосам прямоугольного сечения. Табл.9 служит для расчета жестких полос для наиболее важного случая нагрузки сосредоточенной силой, приложенной в любом сечении полосы.
Таблица имеет два входа: по α, приведенным к полудлине полосы l – абсциссы точек приложения нагрузки, и по ξ, приведенным к l – абсциссы сечений, для которых устанавливается расчетная величина. Начало отсчета – середина полосы, при этом принимается, что для сечений, расположенных правее середины полосы, значения ξ положительны, а левее – отрицательны. Величины α и ξ округляются до первого знака после запятой.
В таблице приведены ординаты безразмерных величин 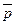 ,
, 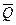 ,
, 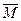 , которые позволяют определять истинные значения реактивных давлений р, поперечных сил Q и изгибающих моментов М с помощью равенств:
, которые позволяют определять истинные значения реактивных давлений р, поперечных сил Q и изгибающих моментов М с помощью равенств:
р = р 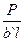 (кПа); Q =
(кПа); Q = 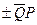 (кН); М =
(кН); М =  (кН·м) (138)
(кН·м) (138)
(подразумевается, что сила Р дана в кН, а полудлина – в м).
В таблицах для 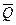 звездочкой отмечены значения слева от силы Р. Справа значения
звездочкой отмечены значения слева от силы Р. Справа значения 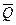 будут
будут 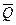 =
= 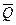 * - 1. Если сила приложена в левой половине полосы в таблице для
* - 1. Если сила приложена в левой половине полосы в таблице для 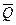 , все значения меняют знак на обратный.
, все значения меняют знак на обратный.
Полосы считаются имеющими конечную длину и жесткость в случае, если их показатель гибкости удовлетворяет неравенству
1 ≤ t ≤ 10 (139)
Наконец, длинные полосы, когда t > 10, при расчете приближенно принимаются либо за бесконечно длинные, либо за полубесконечные. Полоса считается бесконечной, когда сила Р приложена на расстоянии аl от левого конца полосы и на расстоянии аr от правого конца, удовлетворяющих неравенствам:
α l = al/L ≥ 2; α r = ar/L ≥ 2, (140)
где L – упругая характеристика балки, м:
L = 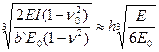 . (141)
. (141)
В случае если неравенство (140) справедливо лишь для или только для ar, полоса называется полубесконечной.
Если полоса загружена рядом сосредоточенных сил, то определяются эпюры от каждой силы в отдельности, а затем они суммируются.
Расчет балок в условиях пространственной задачи. В этом случае метод расчета также зависит от показателя гибкости балки
t = 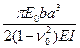 , (142)
, (142)
где а и b – полудлина и полуширина балки.
Балка принимается за жесткую, если показатель гибкости t ≤ 0,5. Балка принимается за длинную, если
λ = а/L; β = b/L = b `/(2 L); b ` = 2 b, (143)
где L определяется равенством (141),
и удовлетворяются условия:
при 0,01 < β < 0,15 λ > 1
0,15 < β < 0,3 λ > 2
0,3 < β < 0,5 λ > 3,5
Остальные балки рассчитываются как короткие, т.е. имеющие конечную длину и жесткость.
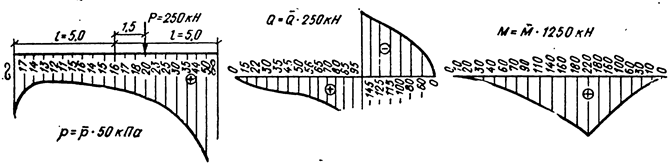 |
Т А Б Л И Ц А 9. БЕЗРАЗМЕРНЫЕ ЭПЮРЫ ДЛЯ ЖЕСТКОЙ ПОЛОСЫ ШИРИНОЙ b `=1 м, НАГРУЖЕННЫЕ СОСРЕДОТОЧЕННОЙ СИЛОЙ Р, кН
| α | ξ | α | ||||||||||||||||||||
| -1,0 | -0,9 | -0,8 | -0,7 | -0,6 | -0,5 | -0,4 | -0,3 | -0,2 | -0,1 | 0,0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | ||
| р | ||||||||||||||||||||||
| 0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 | ∞ ∞ ∞ ∞ ∞ -∞ -∞ -∞ -∞ -∞ | 0,73 0,60 0,47 0,34 0,20 0,07 -0,06 -0,19 -0,32 -0,45 -0,58 | 0,53 0,45 0,36 0,28 0,19 0,11 0,02 -0,06 -0,15 -0,23 -0,32 | 0,46 0,38 0,32 0,26 0,20 0,13 0,07 -0,01 -0,05 -0,12 -0,18 | 0,40 0,35 0,30 0,25 0,21 0,16 0,11 0,06 0,02 -0,03 -0,08 | 0,37 0,33 0,29 0,26 0,22 0,18 0,15 0,11 0,07 0,04 | 0,35 0,32 0,29 0,26 0,24 0,21 0,18 0,15 0,12 0,10 0,07 | 0,33 0,31 0,29 0,27 0,25 0,23 0,21 0,19 0,17 0,16 0,13 | 0,32 0,31 0,30 0,29 0,27 0,26 0,25 0,23 0,22 0,21 0,19 | 0,32 0,32 0,31 0,30 0,29 0,29 0,28 0,27 0,27 0,26 0,26 | 0,32 0,32 0,32 0,32 0,32 0,32 0,32 0,32 0,32 0,32 0,32 | 0,32 0,33 0,33 0,34 0,35 0,35 0,36 0,36 0,37 0,38 0,38 | 0,32 0,34 0,35 0,36 0,38 0,39 0,40 0,42 0,43 0,44 0,45 | 0,33 0,35 0,37 0,39 0,41 0,43 0,45 0,47 0,49 0,51 0,53 | 0,35 0,37 0,40 0,43 0,46 0,49 0,51 0,54 0,57 0,60 0,63 | 0,37 0,40 0,44 0,48 0,51 0,55 0,59 0,62 0,66 0,70 0,73 | 0,40 0,45 0,49 0,54 0,59 0,64 0,68 0,73 0,78 0,83 0,87 | 0,45 0,51 0,57 0,63 0,69 0,76 0,82 0,88 0,94 1,01 1,07 | 0,53 0,61 0,70 0,78 0,87 0,95 1,04 1,12 1,21 1,29 1,38 | 0,73 0,86 0,99 1,12 1,26 1,39 1,52 1,65 1,78 1,91 2,04 | ∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞ ∞ | 0,0 -0,1 -0,2 -0,3 -0,4 -0,5 -0,6 -0,7 -0,8 -0,9 -1,0 |
Q
| 0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 | 0,14 0,12 0,09 0,06 0,03 0,00 -0,02 -0,05 -0,08 -0,11 -0,13 | 0,20 0,17 0,13 0,09 0,05 0,01 -0,02 -0,06 -0,10 -0,14 -0,18 | 0,25 0,21 0,16 0,12 0,07 0,03 -0,02 -0,06 -0,11 -0,16 -0,20 | 0,29 0,24 0,19 0,14 0,09 0,04 -0,01 -0,06 -0,11 -0,16 -0,21 | 0,33 0,28 0,22 0,17 0,11 0,07 0,00 -0,06 -0,11 -0,16 -0,22 | 0,37 0,31 0,25 0,19 0,14 0,08 0,02 -0,05 -0,10 -0,16 -0,21 | 0,40 0,34 0,28 0,22 0,16 0,10 0,04 -0,02 -0,08 -0,14 -0,20 | 0,44 0,37 0,31 0,25 0,19 0,12 0,06 0,00 -0,06 -0,13 -0,19 | 0,47 0,40 0,34 0,28 0,21 0,15 0,09 0,02 -0,04 -0,10 -0,16 | 0,50* 0,44 0,37 0,31 0,24 0,18 0,12 0,05 -0,01 -0,07 -0,14 | -0,47 0,47* 0,40 0,34 0,28 0,21 0,15 0,09 -0,02 -0,04 -0,10 | -0,44 -0,50 0,44* 0,38 0,31 0,25 0,19 0,13 0,05 0,00 -0,06 | -0,40 -0,46 -0,52 0,42* 0,35 0,29 0,23 0,17 0,11 0,05 -0,01 | -0,37 -0,43 -0,49 -0,54 0,40* 0,34 0,28 0,22 0,16 0,11 0,05 | -0,33 -0,39 -0,44 -0,50 -0,55 0,39* 0,34 0,28 0,28 0,17 0,21 | -0,29 -0,35 -0,40 -0,45 -0,50 -0,55 0,40* 0,35 0,30 0,25 0,20 | -0,25 -0,30 -0,34 -0,39 -0,43 -0,48 -0,53 0,43* 0,38 0,34 0,29 | -0,20 -0,24 -0,28 -0,32 -0,36 -0,40 -0,43 -0,47 0,49* 0,45 0,41 | -0,14 -0,17 -0,20 -0,23 -0,26 -0,28 -0,31 -0,34 -0,37 0,61* 0,58 | 1* | 0,0 -0,1 -0,2 -0,3 -0,4 -0,5 -0,6 -0,7 -0,8 -0,9 -1,0 |
M
| 0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 | 0,01 0,01 0,01 0,00 0,00 0,00 0,00 0,00 -0,01 -0,01 -0,01 | 0,03 0,02 0,02 0,01 0,01 0,00 0,00 -0,01 -0,01 -0,02 -0,02 | 0,05 0,04 0,03 0,02 0,01 0,00 -0,01 -0,02 -0,02 -0,03 -0,04 | 0,08 0,06 0,05 0,03 0,02 0,01 -0,01 -0,02 -0,04 -0,05 -0,06 | 0,11 0,09 0,07 0,05 0,03 0,02 -0,01 -0,03 -0,03 -0,07 -0,09 | 0,14 0,12 0,09 0,07 0,04 0,03 -0,01 -0,03 -0,06 -0,08 -0,11 | 0,18 0,15 0,12 0,09 0,06 0,04 -0,01 -0,04 -0,07 -0,10 -0,13 | 0,22 0,19 0,15 0,11 0,07 0,05 0,00 -0,04 -0,07 -0,11 0,15 | 0,27 0,23 0,18 0,14 0,09 0,07 0,01 -0,03 -0,08 -0,12 -0,17 | 0,32 0,27 0,22 0,17 0,12 0,09 0,02 -0,02 -0,08 -0,13 -0,18 | 0,27 0,31 0,26 0,20 0,14 0,11 0,03 -0,01 -0,08 -0,14 -0,19 | 0,22 0,26 0,30 0,24 0,17 0,14 0,05 0,00 -0,08 -0,14 -0,20 | 0,18 0,21 0,24 0,28 0,21 0,17 0,07 0,02 -0,07 -0,14 -0,20 | 0,14 0,17 0,19 0,22 0,24 0,21 0,09 0,05 -0,05 -0,13 -0,20 | 0,11 0,13 0,15 0,17 0,19 0,15 0,13 0,08 -0,01 -0,11 -0,20 | 0,08 0,09 0,11 0,12 0,13 0,14 0,16 0,12 -0,02 -0,09 -0,20 | 0,05 0,06 0,07 0,08 0,09 0,05 0,11 0,06 0,02 -0,06 -0,18 | 0,03 0,03 0,04 0,04 0,05 0,02 0,06 0,06 0,07 -0,03 -0,16 | 0,01 0,01 0,01 0,01 0,02 0,02 0,02 0,02 0,02 0,03 -0,12 | 0,0 -0,1 -0,2 -0,3 -0,4 -0,5 -0,6 -0,7 -0,8 -0,9 -1,0 |
ξ
| α | 0,9 | 0,8 | 0,7 | 0,6 | 0,5 | 0,4 | 0,3 | 0,2 | 0,1 | -0,1 | -0,2 | -0,3 | -0,4 | -0,5 | -0,6 | -0,7 | -0,8 | -0,9 | -1 | α |
 |
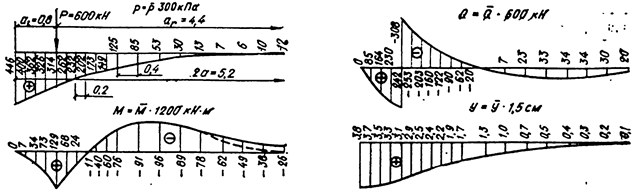
Т А Б Л И Ц А 10. БЕЗРАЗМЕРНЫЕ ЭПЮРЫ ДЛЯ ПОЛУБЕСКОНЕЧНЫХ ПОЛОС ШИРИНОЙ b `=1 м, НАГРУЖЕННЫХ СОСРЕДОТОЧЕННОЙ СИЛОЙ Р, кН
| α | ξ | |||||||||||||||||||||
| 0,2 | 0,4 | 0,6 | 0,8 | 1,0 | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 | 2,2 | 2,4 | 2,6 | 2,8 | 3,0 | 3,2 | 3,4 | 3,6 | 3,8 | 4,0 | |||
| р | ||||||||||||||||||||||
| 0,2 0,4 0,6 0,8 1,0 1,2 1,4 1,6 1,8 2,0 | - - - - - - - - - - - | 1,27 1,12 0,96 0,80 0,66 0,53 0,42 0,32 0,24 0,17 0,12 | 0,76 0,71 0,66 0,59 0,51 0,43 0,36 0,29 0,24 0,18 0,14 | 0,50 0,51 0,51 0,50 0,46 0,41 0,36 0,30 0,26 0,21 0,17 | 0,34 0,37 0,40 0,42 0,43 0,41 0,37 0,33 0,28 0,24 0,20 | 0,23 0,27 0,31 0,35 0,38 0,40 0,38 0,35 0,32 0,28 0,24 | 0,15 0,20 0,24 0,29 0,34 0,37 0,39 0,38 0,35 0,31 0,28 | 0,09 0,14 0,19 0,24 0,29 0,33 0,37 0,39 0,38 0,35 0,31 | 0,05 0,09 0,14 0,19 0,24 0,29 0,33 0,37 0,39 0,38 0,35 | 0,02 0,06 0,11 0,16 0,20 0,25 0,29 0,34 0,37 0,39 0,38 | -0,01 0,04 0,08 0,12 0,17 0,21 0,26 0,30 0,34 0,37 0,39 | -0,02 0,02 0,06 0,09 0,13 0,18 0,22 0,26 0,30 0,34 0,37 | -0,03 0,00 0,04 0,07 0,11 0,14 0,18 0,22 0,26 0,30 0,34 | -0,04 -0,01 0,02 0,05 0,08 0,12 0,15 0,19 0,23 0,27 0,30 | -0,04 -0,01 0,01 0,04 0,06 0,09 0,12 0,16 0,19 0,23 0,27 | -0,04 -0,02 0,00 0,02 0,05 0,07 0,10 0,13 0,16 0,19 0,23 | -0,04 -0,02 0,00 0,02 0,04 0,06 0,08 0,10 0,13 0,16 0,19 | -0,04 -0,02 0,00 0,02 0,02 0,04 0,06 0,08 0,10 0,13 0,167 | -0,03 -0,02 -0,01 0,00 0,02 0,03 0,05 0,06 0,08 0,11 0,13 | -0,03 -0,02 -0,01 0,00 0,01 0,02 0,03 1,05 0,06 1,08 0,11 | -0,03 -0,02 -0,01 0,00 0,00 0,01 0,02 0,04 0,05 0,07 0,08 | |
| Q | ||||||||||||||||||||||
| 0,0 0,2 0,4 0,6 0,8 1,0 1,2 1,4 1,6 1,8 2,0 | -0,44 0,47* 0,40 0,32 0,25 0,20 0,15 0,11 0,07 0,05 0,03 | -0,25 -0,35 0,55* 0,45 0,36 0,29 0,22 0,17 0,12 0,08 0,05 | -0,12 -0,23 -0,33 0,56* 0,46 0,37 0,29 0,23 0,17 0,12 0,08 | -0,04 -0,14 -0,24 -0,35 0,55* 0,45 0,37 0,29 0,22 0,17 0,12 | -0,02 -0,08 -0,17 -0,27 -0,37 0,53* 0,44 0,36 0,28 0,22 0,17 | 0,05 -0,03 -0,11 -0,21 -0,30 -0,39 0,52* 0,43 0,35 0,28 0,22 | 0,08 0,00 -0,07 -0,15 -0,24 -0,32 -0,40 0,51* 0,42 0,34 0,28 | 0,09 0,02 -0,04 -0,11 -0,18 -0,26 -0,33 -0,42 0,50* 0,42 0,34 | 0,10 0,04 -0,01 -0,08 -0,14 -0,20 -0,27 -0,34 -0,42 0,50* 0,41 | 0,10 0,05 0,00 -0,05 -0,10 -0,16 -0,22 -0,28 -0,35 -0,43 0,49* | 0,09 0,05 0,01 -0,03 -0,07 -0,12 -0,17 -0,23 -0,26 -0,36 -0,43 | 0,09 0,06 0,02 -0,01 -0,05 -0,09 -0,13 -0,18 -0,21 -0,29 -0,36 | 0,08 0,06 0,03 0,00 -0,03 -0,06 -0,10 -0,14 -0,17 -0,23 -0,29 | 0,08 0,05 0,03 0,01 -0,01 -0,04 -0,07 -0,10 -0,13 -0,18 -0,24 | 0,07 0,05 0,03 0,02 0,00 -0,02 -0,05 -0,07 -0,10 -0,14 -0,19 | 0,06 0,05 0,03 0,02 0,01 -0,01 -0,03 -0,05 -0,07 -0,11 0,14 | 0,05 0,04 0,03 0,02 0,01 0,00 -0,02 -0,03 -0,05 -0,08 -0,11 | 0,04 0,04 0,03 0,02 0,02 0,01 0,00 -0,02 -0,03 -0,06 -0,08 | 0,04 0,03 0,03 0,02 0,02 0,01 0,00 -0,01 -0,02 -0,04 -0,06 | 0,03 0,03 0,03 0,02 0,02 0,02 0,01 0,00 -0,01 -0,02 -0,04 | ||
| M | ||||||||||||||||||||||
| 0,0 0,2 0,4 0,6 0,8 1,0 1,2 1,4 1,6 1,8 2,0 | -0,12 0,06 0,05 0,04 0,03 0,03 0,02 0,01 0,01 0,01 0,00 | -0,19 -0,02 0,15 0,12 0,10 0,07 0,06 0,04 0,03 0,01 0,01 | -0,23 -0,08 0,07 0,22 0,17 0,14 0,11 0,08 0,06 0,04 0,02 | -0,24 -0,12 0,01 0,14 0,27 0,22 0,17 0,13 0,10 0,07 0,04 | -0,24 -0,14 -0,03 0,08 0,20 0,32 0,25 0,20 0,15 0,10 0,07 | -0,24 -0,15 -0,06 0,03 0,13 0,24 0,35 0,31 0,21 0,16 0,11 | -0,22 -0,15 -0,08 0,00 0,08 0,16 0,26 0,37 0,29 0,22 0,16 | -0,21 -0,15 -0,09 -0,03 0,04 0,11 0,19 0,28 0,38 0,30 0,22 | -0,19 -0,15 -0,10 -0,05 0,00 0,06 0,13 0,20 0,29 0,39 0,30 | -0,17 -0,14 -0,10 -0,06 0,02 0,03 0,08 0,14 0,21 0,29 0,39 | -0,15 -0,12 -0,11 -0,07 -0,04 0,00 0,04 0,09 0,15 0,22 0,30 | -0,13 -0,11 -0,11 -0,07 -0,05 -0,02 0,01 0,05 0,10 0,15 0,22 | -0,12 -0,10 -0,10 -0,07 -0,06 -0,04 -0,01 0,02 0,05 0,10 0,15 | -0,10 -0,09 -0,09 -0,07 -0,06 -0,05 -0,03 -0,01 0,02 0,06 0,10 | -0,09 -0,08 -0,08 -0,07 -0,06 -0,05 -0,04 -0,02 0,00 0,02 0,06 | -0,07 -0,07 -0,07 -0,06 -0,06 -0,06 -0,05 -0,04 -0,02 0,00 0,02 | -0,06 -0,06 -0,06 -0,06 -0,06 -0,06 -0,05 -0,04 -0,03 -0,02 0,00 | -0,05 -0,05 -0,05 -0,06 -0,06 -0,06 -0,05 -0,05 -0,04 -0,04 -0,02 | -0,04 -0,05 -0,05 -0,05 -0,05 -0,05 -0,05 -0,05 -0,05 -0,04 -0,03 | -0,04 -0,04 -0,04 -0,05 -0,05 -0,05 -0,05 -0,05 -0,05 -0,05 -0,04 | ||
 |
Т А Б Л И Ц А 11. БЕЗРАЗМЕРНЫЕ ЭПЮРЫ ДЛЯ ДЛИННЫХ БАЛОК НА УПРУГОМ ОСНОВАНИИ
| ξ | α | |||||||||||
| 0,0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | ∞ | |
| При β=0,025 р | ||||||||||||
| 0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,2 1,4 1,6 1,8 2,0 2,2 2,4 2,6 2,8 3,0 | 3,227 2,626 2,105 1,658 1,282 0,963 0,698 0,481 0,306 0,165 0,057 -0,085 -0,152 -0,170 -0,158 -0,134 -0,106 -0,076 -0,052 -0,032 -0,021 | 2,747 2,296 1,895 1,538 1,229 0,959 0,730 0,538 0,376 0,246 0,141 -0,003 -0,083 -0,115 -0,121 -0,109 -0,091 -0,068 -0,050 -0,033 -0,020 | 2,259 1,963 1,683 1,421 1,182 0,962 0,768 0,603 0,454 0,328 0,230 0,079 -0,012 -0,062 -0,083 -0,084 -0,074 -0,059 -0,045 -0,033 -0,020 | 1,828 1,644 1,465 1,291 1,121 0,958 0,802 0,660 0,528 0,413 0,314 0,160 0,057 -0,006 -0,040 -0,056 -0,058 -0,051 -0,012 -0,033 -0,024 | 1,402 1,335 1,248 1,159 1,059 0,947 0,831 0,715 0,601 0,494 0,401 0,243 0,127 0,047 -0,003 -0,030 -0,042 -0,043 -0,039 -0,035 -0,023 | 1,101 1,057 1,034 1,106 0,967 0,911 0,839 0,755 0,665 0,575 0,484 0,325 0,199 0,106 0,043 0,002 -0,023 -0,034 -0,035 -0,035 -0,034 | 0,867 0,825 0,829 0,846 0,857 0,851 0,826 0,772 0,714 0,645 0,563 0,409 0,275 0,167 0,089 0,035 -0,002 -0,019 -0,031 -0,034 -0,040 | 0,723 0,643 0,643 0,680 0,727 0,765 0,775 0,772 0,745 0,703 0,634 0,494 0,353 0,233 0,141 0,073 0,024 -0,008 -0,017 -0,032 -0,044 | 0,570 0,482 0,480 0,537 0,588 0,669 0,723 0,750 0,757 0,742 0,693 0,576 0,432 0,300 0,192 0,110 0,051 0,013 -0,013 -0,031 -0,042 | 0,434 0,340 0,345 0,395 0,480 0,569 0,649 0,711 0,751 0,759 0,737 0,650 0,507 0,367 0,213 0,149 0,079 0,028 -0,009 -0,031 -0,039 | 0,273 0,219 0,226 0,284 0,371 0,471 0,573 0,659 0,724 0,756 0,762 0,712 0,583 0,438 0,301 0,192 0,111 0,050 -0,003 -0,031 -0,030 | 0,761 0,733 0,668 0,602 0,552 0,509 0,456 0,388 0,310 0,233 0,164 0,065 0,013 -0,009 -0,016 -0,016 -0,014 -0,012 -0,009 -0,007 -0,005 |
| М | ||||||||||||
| 0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,2 1,4 1,6 1,8 2,0 2,2 2,4 2,6 2,8 3,0 | -0,085 -0,142 -0,181 -0,202 -0,209 -0,207 -0,198 -0,185 -0,168 -0,150 -0,113 -0,080 -0,050 -0,028 -0,013 -0,004 0,002 0,005 0,006 0,006 | 0,013 -0,050 -0,094 -0,124 -0,142 -0,150 -0,150 -0,144 -0,135 -0,124 -0,098 -0,072 -0,054 -0,030 -0,017 -0,007 0,000 0,002 0,004 0,004 | 0,011 0,041 -0,011 -0,050 -0,076 -0,092 -0,102 -0,105 -0,105 -0,100 -0,085 -0,067 -0,048 -0,033 -0,020 -0,011 -0,006 -0,002 0,000 0,002 | 0,007 0,033 0,072 0,026 -0,007 -0,035 -0,054 -0,067 -0,072 -0,074 -0,070 -0,061 -0,048 -0,035 -0,024 -0,015 -0,007 -0,003 0,000 0,001 | 0,007 0,028 0,059 0,104 0,059 0,022 -0,004 -0,024 -0,039 -0,048 -0,056 -0,054 -0,046 -0,035 -0,026 -0,018 -0,011 -0,005 -0,002 0,000 | 0,006 0,022 0,048 0,085 0,131 0,085 0,050 0,020 -0,002 -0,018 -0,039 -0,044 -0,043 -0,071 -0,031 -0,024 -0,017 -0,009 -0,004 -0,001 | 0,006 0,018 0,039 0,068 0,105 0,152 0,107 0,068 0,039 0,015 -0,018 -0,033 -0,039 -0,037 -0,031 -0,024 -0,017 -0,009 -0,006 -0,002 | 0,005 0,015 0,031 0,054 0,085 0,122 0,168 0,120 0,081 0,050 0,004 -0,020 -0,033 -0,035 -0,032 -0,026 -0,018 -0,013 -0,011 -0,002 | 0,004 0,011 0,022 0,041 0,065 0,092 0,131 0,176 0,130 0,189 0,030 -0,007 -0,028 -0,034 -0,035 -0,030 -0,024 -0,017 -0,015 -0,005 | 0,003 0,007 0,017 0,030 0,046 0,070 0,100 0,137 0,179 0,135 0,059 0,011 -0,018 -0,031 -0,035 -0,033 -0,028 -0,020 -0,015 -0,009 | 0,002 0,005 0,011 0,020 0,031 0,048 0,070 0,100 0,137 0,181 0,092 0,031 -0,007 -0,026 -0,035 -0,035 -0,031 -0,024 -0,018 -0,013 | 0,176 0,130 0,091 0,058 0,032 0,011 -0,005 -0,016 -0,023 -0,027 -0,029 -0,028 -0,024 -0,020 -0,016 -0,012 -0,010 -0,008 -0,006 -0,005 -0,004 |
| Q | ||||||||||||
| 0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,2 1,4 1,6 | 0* -0,708 -0,472 -0,284 -0,138 -0,026 0,056 0,113 0,153 0,176 0,187 0,183 0,159 0,146 | 0,252* -0,539 -0,367 -0,229 -0,120 -0,036 0,027 0,073 0,103 0,122 0,135 0,126 0,105 | 0,220 0,393* -0,452 -0,322 -0,215 -0,129 -0,061 -0,009 0,030 0,058 0,088 0,093 0,086 | 0,174 0,330 0,467* -0,413 -0,309 -0,221 -0,149 -0,089 -0,042 -0,006 0,040 0,061 0,065 | 0,137 0,266 0,387 0,497* -0,402 -0,314 -0,237 -0,171 -0,116 -0,072 -0,008 0,028 0,048 | 0,106 0,211 0,313 0,412 0,506* -0,407 -0,328 -0,256 -0,194 -0,141 -0,060 -0,009 0,021 | 0,083 0,166 0,250 0,335 0,420 0,504* -0,416 -0,340 -0,272 -0,212 -0,114 -0,047 -0,004 | 0,066 0,128 0,194 0,264 0,340 0,417 0,495* -0,427 -0,354 -0,288 -0,174 -0,090 -0,033 | 0,050 0,091 0,146 0,202 0,266 0,386 0,413 0,488* -0,438 -0,365 -0,237 -0,137 -0,064 | 0,038 0,071 0,107 0,150 0,202 0,263 0,333 0,407 0,482* -0,442 -0,303 -0,188 -0,100 | 0,026 0,047 0,072 0,103 0,144 0,197 0,261 0,330 0,402 0,482* -0,373 -0,243 -0,141 | -0,500* -0,425 -0,355 -0,292 -0,234 -0,181 -0,132 -0,090 -0,055 -0,028 -0,008 0,014 0,021 0,021 |
Date: 2015-06-07; view: 1637; Нарушение авторских прав