Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Конечно-разностная аппроксимация
|
|
Пусть нижний индекс соответствует координате, а верхний времени, например 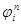 , и кроме того,
, и кроме того, 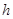 - шаг по координате,
- шаг по координате, 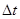 -по времени.
-по времени.
Аппроксимация производных имеет вид:

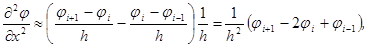
обозначим 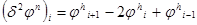 , тогда подстановка в уравнение теплопроводности даёт:
, тогда подстановка в уравнение теплопроводности даёт:
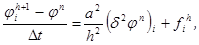
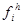 - плотность поверхностных источников,
- плотность поверхностных источников,
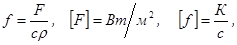
полученную разностную схему перепишем в виде:
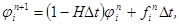
где 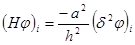 - оператор, действующий на функцию
- оператор, действующий на функцию 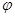 .
.
|
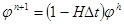 .
.
Явная схема устойчива только при малых шагах по времени. Для повышения устойчивости можно перейти к неявным схемам, например,
 , которую можно переписать как явную
, которую можно переписать как явную
 ,
,
где 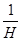 - обратный оператор, эта схема обладает лучшей устойчивостью.
- обратный оператор, эта схема обладает лучшей устойчивостью.
Задание №18. Численное решение уравнения теплопроводности по явной разностной схеме. Выявление неустойчивости.
Уравнение: 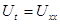 ,
,
Граничные условия: 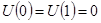 ,
,
Начальное условие  гауссоида, центрированная относительно
гауссоида, центрированная относительно 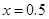
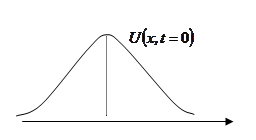 |
Аналитическое решение имеет вид
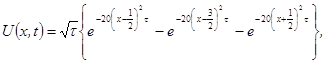 где
где 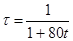 .
.
Задание.
Убедиться, что для шага по времени 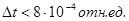 при
при  явная схема работает устойчиво, а при
явная схема работает устойчиво, а при 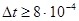 неустойчиво (осцилляции).
неустойчиво (осцилляции).
Задание №19. Остывание шара.
Уравнение теплопроводности имеет вид:
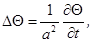
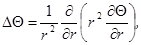 и заменой переменных
и заменой переменных 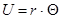 приводится к виду:
приводится к виду:

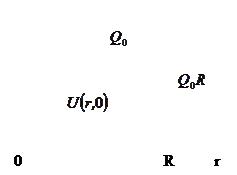
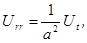 (как плоская стенка)
(как плоская стенка)
 начальное условие:
начальное условие: 
граничные условия: 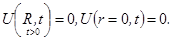
Вариант 1: Вычислить время остывания варённого куриного яйца, 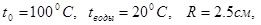
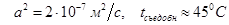 в центре шара. Аналитическое решение даётся интегралом Пуассона
в центре шара. Аналитическое решение даётся интегралом Пуассона
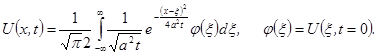
 Вариант 2: За какое время остынет чугунное ядро в центре со
Вариант 2: За какое время остынет чугунное ядро в центре со 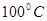 до
до 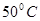 ,
, 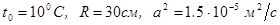 .
.

 Задание №20. Нагревание длинного стержня.
Задание №20. Нагревание длинного стержня.




 Как быстро распространяется температурная волна? Из уравнения
Как быстро распространяется температурная волна? Из уравнения

 теплопроводности- бесконечно быстро, т.е. при
теплопроводности- бесконечно быстро, т.е. при 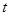 сколь угодно малом,
сколь угодно малом, 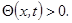
(противоречит молекулярной физике!). Чтобы избежать этого надо брать конечное изменение температуры.
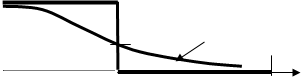
Рассмотрим краевую задачу подробнее, будем считать стержни теплоизолированными от воздуха и пренебрегаем излучением. Соответствует задаче о соприкосновении двух длинных стержней с разностью температур 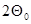 . Начальное условие приближённо имеет вид для правого стержня:
. Начальное условие приближённо имеет вид для правого стержня:
 |
|


{полагая, что стержень тонкий, и источник поддерживает постоянную температуру, получаем граничное условие} 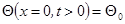 . Для правого конца
. Для правого конца 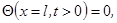 где
где  - длина стержня (это условие приближённое,
- длина стержня (это условие приближённое,  с запасом,
с запасом, 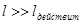 ).
).
Аналитическое решение рассматриваемой задачи имеет вид:
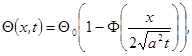 где
где  - функция ошибок,
- функция ошибок, 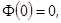 см. Тихонов, Самарский, «Уравнения математической физики», с.233. Найдём скорость температурной волны, для этого приравняем «фазу» в двух близко расположенных точках
см. Тихонов, Самарский, «Уравнения математической физики», с.233. Найдём скорость температурной волны, для этого приравняем «фазу» в двух близко расположенных точках
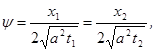 под скоростью будем понимать величину
под скоростью будем понимать величину
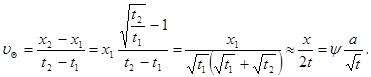
Из полученной формулы видно, что скорость изменения координаты с заданной температурой зависит от материала, например, 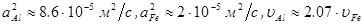 , и, кроме того, скорость уменьшается со временем. Для проверки можно осуществить следующий эксперимент:
, и, кроме того, скорость уменьшается со временем. Для проверки можно осуществить следующий эксперимент:
 |





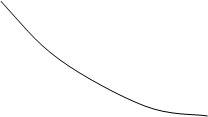


 Можно осуществить такой же компьютерный эксперимент (с графическим изображением падающих кнопок) при повышении
Можно осуществить такой же компьютерный эксперимент (с графическим изображением падающих кнопок) при повышении  , например, на
, например, на  . Отметим, что скорость тепловой волны зависит также от фазы, т.е. от значения температуры, которую мы «ждём» в точке наблюдения.
. Отметим, что скорость тепловой волны зависит также от фазы, т.е. от значения температуры, которую мы «ждём» в точке наблюдения.
Замечания по поводу численной реализации алгоритма.
При задании граничного условия 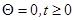 на свободной границе вносится дополнительная погрешность, снизить которую можно или «удлинением стержня» или переформулировкой граничного условия.
на свободной границе вносится дополнительная погрешность, снизить которую можно или «удлинением стержня» или переформулировкой граничного условия.
В первом случае запас по длине нужно выбирать с учётом допустимой погрешности решения. В нашем случае помогает анализ аналитического решения:
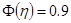 при
при 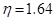 , при этом
, при этом 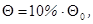
 при
при 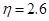 , при этом
, при этом 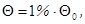
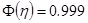 при
при 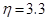 , при этом
, при этом 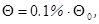
таим образом, достаточно выбрать 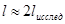 .
.
Во втором случае можно, например, ввести бесконечный граничный элемент, тогда:
|



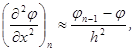
 будет оказывать демпфирующее воздействие на
будет оказывать демпфирующее воздействие на 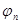 . Во втором случае длину можно ограничить
. Во втором случае длину можно ограничить 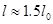 . Хорошо бы сравнить численные результаты.
. Хорошо бы сравнить численные результаты.
Date: 2015-05-04; view: 877; Нарушение авторских прав
 , выражение
, выражение 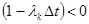 , при уменьшении
, при уменьшении 
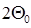
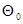
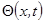 Х
правый стержень
Х
правый стержень