Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Дизъюнктивные и конъюнктивные нормальные формы. Совершенные конъюнктивные и дизъюнктивные нормальные формы
|
|
Элементарной конъюнкцией называется конъюнкция, состоящая только из переменных или их отрицаний. Например: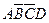 
.
Дизъюнктивно-нормальной формой (ДНФ) называется дизъюнкция элементарных конъюнкций. Например: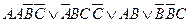 
.
Если учесть, что нулевые конъюнкции можно опустить, а А*А=А, то приведенная ДНФ сведется к более простому виду: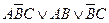 
. Дальнейшее упрощение получается с помощью законов поглощения: 
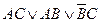. Но полученная формула еще не является минимальной. Можно применить правило, основанное на соображениях симметрии: в рассматриваемой формуле каждая из переменных А, В, встречается два раза, но переменная В встречается один раз с отрицанием, а один раз без отрицания. Значит, симметрия нарушена по переменной В. Тогда тот член дизъюнкции, который эту переменную В не содержит, пропадет, т. е. поглотится АС.
Покажем, что это действительно так:
= 
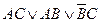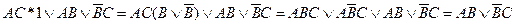
(по закону поглощения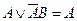 
).
Мы доказали следующее правило поглощения:
Если ДНФ является трехчленом, зависящим от трех переменных, и если симметрия нарушена только по одной из переменных, то пропадает тот член дизъюнкции, который эту переменную не содержит.
Проиллюстрируем это правило еще на двух примерах.
1. 
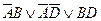. Этот трехчлен содержит два раза 
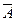, два раза 
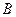, но один раз 
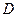и один раз 
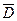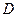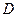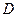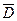. Значит,, симметрия нарушена по . Поэтому, согласно нашему правилу, пропадает член, не содержащий букву (т. е. не содержащий ни , ни ). Значит, надо вычеркнуть 
.
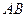2. 
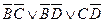. Этот трехчлен содержит два раза 
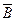, два раза 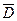, но один раз 
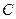и один раз 
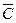. Симметрия нарушена по 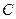. Значит, вычеркиваем член, не содержащий 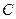, т. е. вычеркиваем 
.
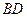Минимальной мы назовемту ДНФ, которая имеет самую короткую запись.
Существует еще одно правило поглощения, которое тоже основано на соображениях симметрии:
Если ДНФ является трехчленом, зависящим от трех переменных, и если симметрия нарушена по двум из этих переменных, то данная ДНФ равносильна дизъюнкции, одним из членов которой является переменная, по которой симметрия не нарушена, а вторым членом служит тот член первоначальной ДНФ, который эту переменную не содержит.
Например: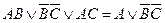 
. Покажем, что это действительно так:
.
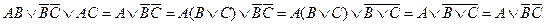Рассмотрим еще несколько примеров, иллюстрирующих это правило.
1. 
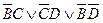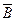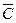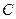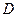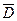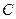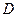. Этот трехчлен содержит два раза , но содержит по одному разу и , и по одному разу и . Значит, симметрия нарушена дважды: по и по . Симметрия не нарушена только по 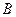. Поэтому, применяя наше правило, получим дизъюнкцию, одним членов которой будет 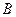, а другим — тот член трехчлена, | который_ не содержит 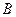. Значит, получим 
.
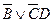2. 
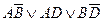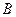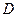. В этом трехчлене симметрия нарушена по и по . Симметрия не нарушена только по 
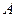. Значит, = 
.
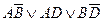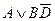Для каждой формулы существует бесконечно много различных, но равносильных ей ДНФ. Если, например, найдена одна ДНФ, то путем повторения имеющихся элементарных конъюнкций, добавления нулевых конъюнкций, добавления поглощаемых конъюнкций можно построить бесконечно много новых, но равносильных ей ДНФ.
Например: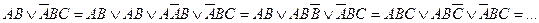 
Среди всех этих ДНФ есть одна, которая отличаете однородностью и «совершенством» своей формы. Mы имеем в виду формулу: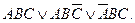 
Она так и называется: «совершенная дизъюнктивно-нормальная форма» (СДНФ).
Дадим точное определение:
СДНФ — это такая ДНФ, которая удовлетворяет следующим условиям:
1. Все элементарные конъюнкции различны.
2. Нет нулевых конъюнкций.
3. Ни одна из элементарных конъюнкций не содержит одинаковых членов.
4. Каждая элементарная конъюнкция содержит все переменные.
Чтобы получить СДНФ, надо сначала найти минимальную ДНФ. Тогда будут выполнены условия 1, 2, 3. Посли этого надо преобразовать эту минимальную ДНФ таким образом, чтобы было выполнено условие 4. Это делается следующим образом:
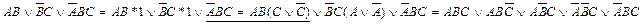Приведение формул алгебры высказываний к КНФ виду
Элементарной дизъюнкцией называется дизъюнкция, состоящая только из переменных или их отрицаний. Например: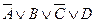 
.
Конъюнктивной нормальной формой (КНФ) называется конъюнкция элементарных дизъюнкций. Например: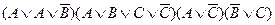 
. Если воспользоваться равносильностью 
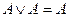, то 
можно заменить через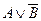 
. Кроме того, известно, что, 
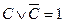. А если один член дизъюнкции равен 1, то и вся дизъюнкция равна 1. Значит: 
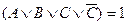. Но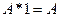 
. Значит, единичный член конъюнкции можно просто опустить. Таким образом, первоначальная КНФ| сводится к более простой форме: 
.
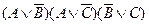Но эта формула не является еще минимальной. Для КНФ тоже существуют правила поглощения, основанные на соображениях симметрии. Эти правила можно получить по закону двойственности из аналогичных правил, установленных для ДНФ.
Мы знаем, например, что: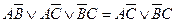 
(симметрия нарушена по переменной 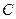. Поглотилось выражение, не содержащее эту переменную). Запишем теперь двойственную равносильность: 
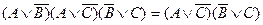. В левой части стоит ранее полученная КНФ. Значит, эту КНФ действительно можно свести к более простой форме.
В то же время мы установили новое правило поглощения:
Если КНФ зависит от трех переменных и представляет собой конъюнкцию трех элементарных дизъюнкций и если симметрия нарушена только по одной из переменных, то поглощается та элементарная дизъюнкция, которая эту переменную не содержит.
Аналогичным образом можно получить и второе правило поглощения, основанное на соображениях симметрии. Мы уже знаем, что: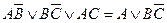 
.
Запишем двойственную равносильность: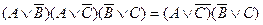 
Сформулируем соответствующее правило поглощения:
Если КНФ зависит от трех переменных и представляет собой конъюнкцию трех элементарных дизъюнкций и если симметрия нарушена по двум из этих переменных, то данная КНФ равносильна конъюнкции, одним из членов которой является переменная, по которой симметрия не нарушена, а вторым членом является тот член первоначальной КНФ, который эту переменную не содержит.
Date: 2015-06-06; view: 1111; Нарушение авторских прав