Квантово механическая теория атома водорода

В атоме водорода или водородоподобном ионе потенциальная энергия электрона равна 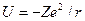, где Ze – заряд ядра, r – расстояние между ядром и электроном. Уравнение Шредингера в этом случае имеет вид:

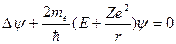. (1)

Поскольку поле является центрально-симметричным, удобно воспользоваться сферической системой координат: 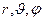. Подставив в (1) выражение оператора Лапласа в сферических координатах, получим уравнение:

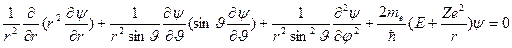. (2)

Можно показать, что уравнение (2) имеет однозначные, конечные и непрерывные решения в следующих случаях:

1) при любых положительных значениях Е;

2) при дискретных отрицательных значениях энергии, равных

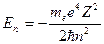(n = 1, 2, 3, …) (3)

Случай Е > 0 соответствует электрону, пролетающему вблизи ядра и удаляющемуся вновь на бесконечность. Случай Е < 0 соответствует электрону, находящемуся в пределах атома. Сравнение (3) с (4) лекции 8 показывает, что квантовая механика приводит к таким же значениям энергии водородного атома, какие получались и в теории Бора. Однако в квантовой механике эти значения получаются логическим путем из основного предположения о том, что движение микрочастиц описывается уравнением Шредингера. Бору же для получения такого результата пришлось вводить специальные дополнительные предположения.

Собственные функции уравнения (2) содержат три целочисленных параметра. Один из них совпадает с номером уровня энергии п, два других принято обозначать буквами l и m. Эти числа называются квантовыми:

n – главное квантовое число,

l – азимутальное квантовое число,

m – магнитное квантовое число.

При данном п числа l и m могут принимать следующие значения:

l = 0, 1, 2,..., n – 1 т. е. всего п различных значений;

m = – l, – l + 1, …–1, 0, +1, …, l – 1, l, т. е. всего 2 l + 1 различных значений.

Таким образом, каждому Е_п (кроме Е ₁) соответствует несколько волновых функций 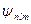, отличающихся значениями квантовых чисел l и m. Это означает, что атом водорода может иметь одно и то же значение энергии, находясь в нескольких различных состояниях.

Состояния с одинаковой энергией называются вырожденными, а число различных состояний с каким-либо значением энергии называется кратностью вырождения соответствующего энергетического уровня. Кратность вырождения уровней водорода легко вычислить, исходя из возможных значений для l и m. Каждому из п значений квантового числа l соответствует 2 l + I значений квантового числа m. Следовательно, число различных состояний, соответствующих данному п, равно .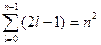

Таким образом, каждый уровень энергии водородного атома имеет вырождение кратности n ².

Е n		n	l	m	В таблице приведены состояния, соответствующие первым трем энергетическим уровням. Как мы выяснили, состояние электрона в водородном атоме зависит от трех квантовых чисел п, l и m, причем значение главного квантового числа п определяет энергию состояния. Естественно предположить, что и два других квантовых числа также определяют какие-то физические величины. Действительно, в квантовой механике доказывается, что азимутальное квантовое число l определяет величину момента импульса электрона в атоме, а магнитное квантовое число m – величину проекции этого момента на заданное направление
Е 1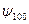
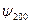
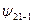
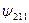
Е 2				–1
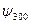
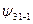
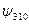
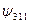
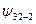
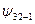
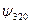
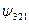
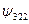
Е 3				–1 –2 –1

в пространстве. Под заданным направлением (мы будем обозначать его буквой z) понимают направление, выделенное физически, путем создания, например, электрического или магнитного поля.

Момент импульса М оказывается равным:

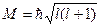. (4)

Проекция момента импульса на заданное направление равна:

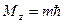. (5)

Соотношения (4) и (5) показывают, что момент импульса электрона в атоме и проекция этого момента являются, как и энергия, квантованными величинами. Постоянную 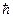можно рассматривать как естественную единицу момента импульса. (Микрочастица, находящаяся в состоянии с отличным от нуля моментом импульса М. обладает также и магнитным моментом m. Направления М и m связаны между собой (в случае электрона эти направления противоположны). Поэтому, проекция m на физически выделенное направление должна также квантоваться. Квантование проекции магнитного момента атома непосредственно обнаруживается в опыте Штерна и Герлаха).

Итак, состояния с различными значениями азимутального квантового числа l отличаются величиной момента импульса. В атомной физике применяются заимствованные из спектроскопии условные обозначения состояний электрона с различными значениями момента импульса. Электрон, находящийся в состоянии с l = 0 называют s-электроном (соответствующее состояние – s-состоянием), с l = 1 – р-электроном, с l = 2 – d-электроном, с l = 3 – f-электроном, затем идут g, h и т. д. уже по алфавиту. Значение главного квантового числа указывается перед условным обозначением квантового числа l. Таким образом, электрон в состоянии с п = 3 и l = 1 обозначается символом Зр и т. д. Поскольку l всегда меньше п, возможны следующие состояния электрона:

1s, 2s, 2p, 3s, 3p, 3d, 4s, 4p, 4d, 4f и т. д.

Схема уровней энергии атома показана на рис. 1. На этой схеме отражено (правда, частично) вырождение уровней; кроме того, она имеет еще ряд существенных преимуществ, по сравнению с приводимой ранее (лекция 8), которые вскоре станут очевидными.

Мы знаем, что испускание и поглощение света происходит при переходах электрона с одного уровня на другой. В квантовой механике доказывается, что возможны только такие переходы, при которых квантовое число l изменяется на единицу:

D l = ±1. (6)

Условие, выраженное соотношением (6), называется правилом отбора. Существование правила (6) обусловлено тем, что фотон обладает собственным моментом импульса (спином), равным примерно 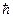(в дальнейшем мы уточним его значение). При испускании фотон уносит из атома этот момент, а при поглощении привносит, так что правило отбора (6) есть просто следствие закона сохранения момента импульса.

На рис. 1 показаны переходы, разрешенные правилом (6). Пользуясь условными обозначениями состояний электрона, переходы, приводящие к возникновению серии Лаймана, можно записать в виде:

np ® 1s (n = 2, 3, 4, …).

Cерии Бальмера соответствуют переходы:

ns ® 2p и nd ® 2p (n = 3, 4, 5, …).

и т. д.

Состояние 1s является основным состоянием атома водорода. В этом состоянии атом обладает минимальной энергией. Чтобы перевести атом из основного состояния в возбужденное (т. е. в состояние с большей энергией), ему необходимо сообщить энергию. Это может быть Осуществлено за счет теплового соударения атомов (по этой причине нагретые тела светятся – атомы излучают, возвращаясь из возбужденного в основное состояние), или

за счет столкновения атома с достаточно быстрым электроном, или, наконец, за счет поглощения атомом фотона.

Фотон при поглощении его атомом исчезает, передавая атому всю свою энергию. Атом не может поглотить только часть фотона, ибо фотон, как и электрон, как и другие элементарные частицы, является неделимым. Поэтому атом может поглощать только те фотоны, энергия которых в точности соответствует разности энергий двух его уровней. Поскольку поглощающий атом обычно находится в основном состоянии, спектр поглощения водородного атома должен состоять из линий, соответствующих переходам:

1s ® np.

Этот результат полностью согласуется с опытом.

Собственные функции s-состояний (т. е. состояний с l = 0) оказываются не зависящими от углов 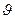и 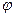. Это можно записать следующим образом:

.

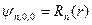Вероятность найти электрон в тонком шаровом слое радиуса r и толщины dr равна:

.

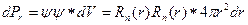Выражение 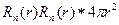представляет собой плотность вероятности нахождения электрона на расстоянии r от ядра.

Волновые функции для l, отличных от нуля, распадаются на два множителя, один из которых зависит только от r, а другой – только от углов и 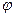. Таким образом, и в этом случае можно ввести понятие плотности вероятности нахождения электрона на расстоянии r от ядра, подразумевая под R(r) ту часть функции 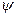которая зависит только от r.

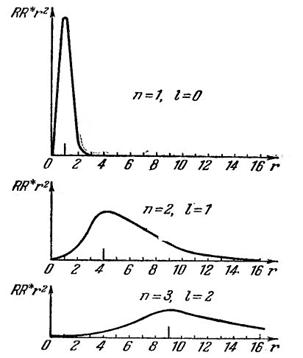
На рис. 2 приведены плотности вероятности для случаев 1) n= 1, l = 0; 2) п = 2, l = 1 и 3) п = 3, l = 2. За единицу масштаба для оси r принят радиус первой боровской орбиты. На графиках отмечены радиусы соответствующих боровских орбит. Как видно из рисунка, эти радиусы совпадают с наиболее вероятными расстояниями электрона от ядра.

Date: 2015-05-04; view: 816; Нарушение авторских прав