Частица в бесконечно глубокой одномерной потенциальной яме. Прохождение частиц через потенциальный барьер

Чтобы пояснить сказанное в предыдущем параграфе, рассмотрим конкретный пример, достаточно простой для того, чтобы уравнение Шредингера можно было легко решить.

Исследуем поведение частицы в бесконечно глубокой одномерной потенциальной яме. Предположим, что частица может двигаться только вдоль оси х. Пусть движение ограничено непроницаемыми для частицы стенками: х = 0 и х = l. Потенциальная энергия U имеет в этом случае следующий вид (рис. 8, а): она равна нулю при 0 < х < l и обращается в бесконечность при х < 0 и х > l.

Поскольку функция 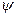зависит только от одной координаты х, уравнение (4) будет иметь вид:

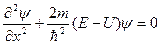. (10)

За пределы потенциальной ямы частица попасть не может, поэтому вероятность обнаружить частицу, а следовательно и 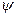-функция за пределами ямы равна нулю. Далее, из условия непрерывности следует, что 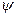должна быть равна нулю и на границах ямы:

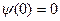и 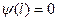. (11)

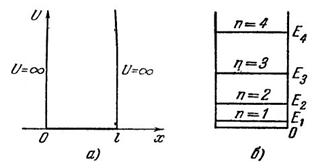Рис. 8.

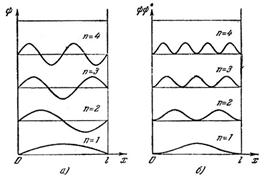Рис. 9.

Выражения (11) и определяют те условия, которым должны удовлетворять решения уравнения (10), имеющие физический смысл. В области, где 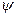не равна тождественно нулю, уравнение (10) принимает следующий вид:

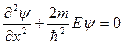. (12)

(U в этой области равна нулю). Введя обозначение 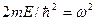получим уравнение, хорошо известное из теории колебаний:

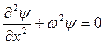. (12)

Решения такого уравнения, как известно, имеют вид:

.

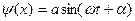Условиям (11) можно удовлетворить соответствующим выбором постоянных 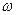и 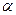. Из условия 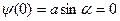получаем, что 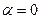. Далее, должно выполняться условие: 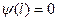, что возможно лишь в случае, если

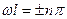(n = 1, 2 3, …) (13)

(n = 0 отпадает, поскольку при этом получается 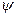тождественно равна нулю и частица нигде не находится).

Из (13) вытекает, что решения уравнения (12) будут иметь физический смысл не при всех значениях энергии Е, а лишь при значениях, удовлетворяющих соотношению:

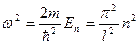(n = 1, 2 3, …).

Таким образом, не прибегая ни к каким дополнительным предположениям (как это пришлось сделать Бору), мы получили квантование энергии частицы и нашли собственные значения этой энергии:

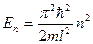(n = 1, 2 3, …). (14)

Схема энергетических уровней изображена на рис. 8, б. Произведем оценку расстояний между соседними уровнями для различных значений массы частицы т и ширины ямы l. Разность энергий двух соседних уровней равна 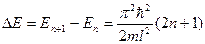. Если взять т порядка массы молекулы, а l порядка 10 см (молекулы газа в сосуде), получается энергия ~10^-32 n эрг. Столь густо расположенные энергетические уровни будут практически восприниматься как сплошной спектр энергии, так что хотя квантование энергии в принципе будет иметь место, но на характере движения молекул сказываться не будет.

Аналогичный результат получается, если взять т порядка массы электрона при тех же размерах ямы (свободные электроны в металле). В этом случае 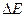будет иметь порядок 10^-28 n эрг или 10^-16 n эВ.

Однако совсем иной результат получается для электрона, если область, в пределах которой он движется, будет порядка атомных размеров (10^-8см). В этом случае 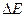будет иметь порядок 10^-10 n эрг или 10² n эВ. Очевидно, что в этом случае дискретность энергетических уровней будет проявляться весьма заметным образом.

Собственными функциями, как следует из условия (13), будут

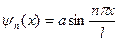. (15)

Для нахождения коэффициента а воспользуемся условием нормировки (9), которое в данном случае запишется следующим образом:

.

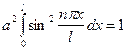На концах промежутка интегрирования подынтегральная функция обращается в нуль. Поэтому значение интеграла можно получить, умножив среднее значение 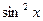(равное, как известно, 1/2) на длину промежутка l. В результате получится: 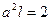, откуда 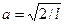. Таким образом, собственные функции имеют вид:

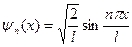(n = 1, 2, 3, …) (16)

Графики функций (16) изображены на рис. 9, а. На рис. 9, б дана плотность вероятности обнаружения частицы на различных расстояниях от стенок ямы,
равная 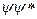. Как следует из графиков, частица в состоянии при п = 2 не может быть обнаружена в середине ямы и вместе с тем одинаково часто бывает как в левой, так и в правой половине ямы. Такое поведение частицы, очевидно, не совместимо с представлением о траекториях. Отметим, что согласно классическим представлениям все положения частицы в яме равновероятны.

6. Прохождение частицы через барьер

Пусть частица, движущаяся слева направо, падает на потенциальный барьер высоты U ₀ и ширины l (рис. 10). По классическим представлениям поведение частицы имеет следующий характер. Если энергия частицы больше высоты барьера (Е > U ₀). частица беспрепятственно проходит «над» барьером (на участке 0 < x < l)лишь уменьшается скорость частицы, но затем при x > l снова принимает первоначальное значение). Если же Е меньше U₀ (как изображено на рисунке), то частица отражается от барьера и летит в обратную сторону; сквозь барьер частица проникнуть не может.

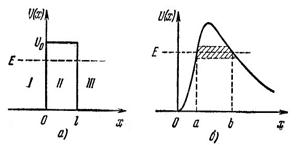Рис. 10.

Иначе выглядит поведение частицы согласно квантовой механике. Во-первых, даже при Е > U ₀ имеется отличная от нуля вероятность того, что частица отразится от барьера и полетит в обратную сторону. Во-вторых, при Е < U₀ имеется отличная от нуля вероятность того, что частица проникнет «сквозь» барьер и окажется в области, где x > l. Такое, совершенно невозможное с классической точки зрения, поведение микрочастицы вытекает непосредственно из решения уравнения Шредингера.

Рассмотрим случай Е < U ₀. В этом случае уравнение Шредингера имеет вид:

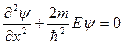(17)

для областей I и III и вид

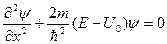(18)

для области II, причем Е – U ₀ < 0.

Легко убедиться (хотя бы подстановкой), что общее решение уравнения Шредингера для каждой из трех областей будет иметь вид:

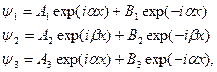
Заметим, что решение вида 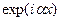соответствует волне, распространяющейся в направлении оси х, а решение вида 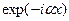волне, распространяющейся в противоположном направлении. Поскольку в области III имеется только волна, прошедшая через барьер и распространяющаяся слева направо, коэффициент В ₃ = 0. Для нахождения остальных коэффициентов необходимо воспользоваться граничными условиями.

После решения системы уравнений для коэффициента прозрачности получается:

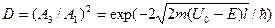. (19)

Как следует из полученного выражения, вероятность прохождения частицы через потенциальный барьер сильно зависит от ширины барьера l и от его превышения над Е, т. е. от (U ₀ – E) Если при какой-то ширине барьера коэффициент прохождения D=А₃/А₁ равен, допустим, 0,01, то при увеличении ширины в два раза D станет равным 0,0001, т.е. уменьшается в 100 раз. Тот же эффект в этом случае вызвало бы возрастание в четыре раза величины (U ₀ – E) Коэффициент прохождения резко уменьшается при увеличении массы частицы т.

В случае потенциального барьера произвольной формы (см., например, рис. 10, б) формула (19) должна быть заменена более общей формулой:

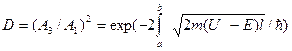, (20)

где U = U(x).

При преодолении потенциального барьера частица как бы проходит через «туннель» в этом барьере (заштрихованная область на рис. 10, б), в связи с чем рассмотренное нами явление часто называют туннельным эффектом.

С классической точки зрения туннельный эффект представляется абсурдным, так как частица, «находящаяся в туннеле», должна была бы обладать отрицательной кинетической энергией. Однако туннелирование – явление специфически квантовое, не имеющее аналога в классической физике. В квантовой же механике деление полной энергии на кинетическую и потенциальную не имеет смысла, так как противоречит принципу неопределенности. Действительно, тот факт, что частица обладает определенной кинетической энергией Т, был бы равнозначен тому, что частица имеет определенный импульс р. Аналогично тот факт, что частица имеет определенную потенциальную энергию U, означал бы, что частица находится в точно заданном месте пространства. Поскольку координата и импульс частицы не могут одновременно иметь определенных значений, не могут быть одновременно точно определены Т и U. Таким образом, хотя полная энергия частицы Е имеет вполне определенное значение, она не может быть представлена в виде суммы точно определенных энергий Т и U. Ясно, что при такой ситуации заключение об отрицательности Т в туннеле становится беспочвенным.

Date: 2015-05-04; view: 845; Нарушение авторских прав