
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Строительство
|
|
Методические указания к выполнению контрольной работы № 1
Для направлений бакалавриата:
Строительство
Профиль:
Промышленное и гражданское строительство
Уфа 2012
00УДК 51(07)
ББК 22.1я73,22.161.6
М 54
Рекомендовано к изданию методической комиссией механического факультета (протокол № 9 от 27 июля 2012 года) и заседанием кафедры математики (протокол № 7 от 10 апреля 2012 года)
Составители: доцент Авзалова З.Т.,
ассистент Чистякова С.В.
Рецензент: доцент кафедры физики Белобородова Н.Н.
Ответственный за выпуск: зав. кафедрой математики доцент Лукманов Р.Л.
Порядок выполнения контрольных работ
К выполнению контрольной работы следует приступать после изучения соответствующего теоретического материала по учебнику и лекциям, а также решения задач на практических занятиях.
При выполнении контрольных работ студент должен, руководствоваться следующими указаниями:
каждую работу следует выполнять в отдельной тетради, на передней обложке которой должны быть указаны фамилия и инициалы студента, шифр, номер контрольной работы и дата ее отсылки в институт;
решения всех задач и пояснения к ним должны быть достаточно подробными, рекомендуется делать соответствующие ссылки на вопросы теории с указанием формул, теорем, выводов, которые используются при решении;
все вычисления должны быть приведены полностью, чертежи и графики должны быть выполнены аккуратно, четко, с указанием единиц масштаба, координатных осей, обозначения в задачах должны соответствовать указаниям на чертеже;
для удобства рецензирования преподавателем контрольной работы следует оставлять на каждой странице поля;
после получения отрецензированной работы студент должен исправить в ней все ошибки. В случае незачета студент обязан в кратчайший срок выполнить все требования рецензента и представить работу на повторное рецензирование. Неверно выполненные задачи или вся работа заново решаются в той же тетради, исправление небольших недочетов и ошибок приводится в конце работы. До экзамена необходимо исправить все ошибки и получить зачет. Работы, выполненные небрежно, несамостоятельно, или содержащие задачи не своего варианта, возвращаются без проверки.
В период экзаменационной сессии, на зачете студент обязан представить зачтенную контрольную работу и по требованию преподавателя дать устные пояснения ко всем задачам, содержащимся в работе.
Студент выполняет тот вариант контрольной работы, который соответствует двум последним цифрам i и j его учебного шифра и определяется по схеме данной преподавателем.
Литература.
1. Шипачев В.С. Основы высшей математики. Учебное пособие./ Под редакцией А.Н. Тихонова. -2-е издание, стереотип.- М.: Высш. шк., 1994.-479с.
2. Шипачев В.С. Задачник по высшей математике. Учебное пособие.-2-е издание, испр.-М.: Высш. шк., 2000.-304с.
3. Зайцев И.А. Высшая математика. Учеб. для с/х вузов. 2-е издание, испр.и доп.-М.: Высш. шк., 1998.-409 с.
1 Решить заданную систему уравнений методом Крамера
1) 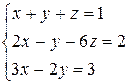 , 2)
, 2) 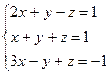 3)
3) 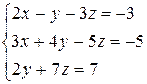 ,
,
4) 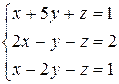 , 5)
, 5) 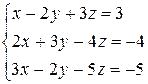 , 6)
, 6) 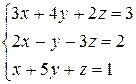 ,
,
7) 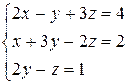 , 8)
, 8) 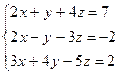 , 9)
, 9) 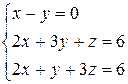 ,
,
10) 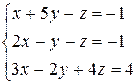 , 11)
, 11) 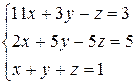 , 12)
, 12) 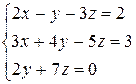 ,
,
13) 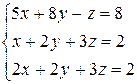 , 14)
, 14) 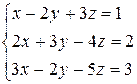 , 15)
, 15) 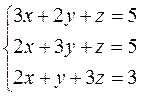 ,
,
16) 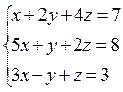 , 17)
, 17) 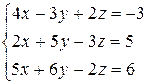 , 18)
, 18) 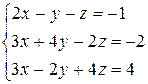 ,
,
19) 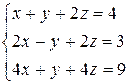 , 20)
, 20) 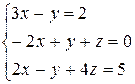 .
.
Решение типовой задачи
Решим систему уравнений с помощью формул Крамера.
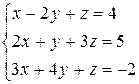
Для этого вычислим главный определитель системы 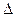 , который составляется из коэффициентов при неизвестных и вычислим его по правилу «треугольников»:
, который составляется из коэффициентов при неизвестных и вычислим его по правилу «треугольников»:
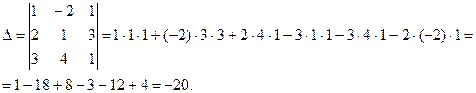
Так как 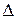 =-20
=-20 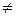 0, делаем вывод о том, что система имеет единственное решение. Для его отыскания вычислим вспомогательные определители
0, делаем вывод о том, что система имеет единственное решение. Для его отыскания вычислим вспомогательные определители 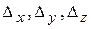 , которые получаются из главного путем замены столбца коэффициентов при соответствующей неизвестной на столбец свободных членов.
, которые получаются из главного путем замены столбца коэффициентов при соответствующей неизвестной на столбец свободных членов.
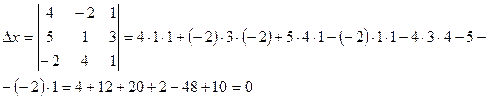
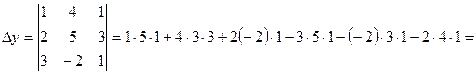
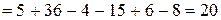
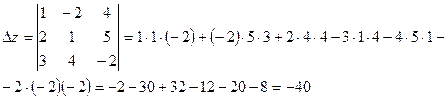
Тогда неизвестные x, y, z по формулам Крамера находятся следующим образом:
х= 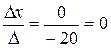 , у=
, у= 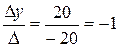 ; z=
; z= 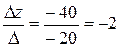 .
.
Сделаем проверку, подставив найденные значения неизвестных в исходную систему:
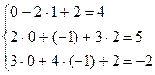 ,
, 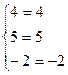
Т.к. все три уравнения обращаются в верные равенства, то решение найдено правильно.
Ответ: (0;-1;-2)
2. В задачах 1-20 даны координаты вершин треугольника АВС. Требуется: 1) длину стороны АВ; 2) уравнение сторон АВ и АС в общем виде и их угловые коэффициенты; 3) угол А в радианах; 4) уравнение медианы АD; 5) уравнение высоты СЕ и ее длину. Сделать чертеж.
| N зад. | А | В | С | N зад. | А | В | С |
| (-7;6) | (2;-6) | (7;4) | (10;8) | (-2;-1) | (8;-6) | ||
| (-5;7) | (4;-5) | (9;5) | (7;9) | (-5;0) | (5;-5) | ||
| (-3;5) | (6;-7) | (11;3) | (9;10) | (-3;1) | (7;-4) | ||
| (-6;10) | (3;-2) | (8;8) | (11;2) | (-1;-7) | (9;-12) | ||
| (-4;8) | (5;-4) | (10;6) | (6;7) | (-6;-2) | (4;-7) | ||
| (-8;9) | (1;-3) | (6;7) | (2;3) | (-10;-6) | (0;-11) | ||
| (-9;12) | (0;0) | (5;10) | (5;4) | (-7;-5) | (3;-10) | ||
| (-2;11) | (7;-1) | (12;9) | (3;6) | (-9;-3) | (1;-8) | ||
| (-1;4) | (8;-8) | (13;2) | (8;5) | (-4;-4) | (6;-9) | ||
| (1;3) | (10;-9) | (15;1) | (4;11) | (-8;2) | (2;-3) |
Решение типовой задачи
Даны вершины треугольника АВС А(-2;5); В(10;-4); С(8;10). Требуется найти: 1) длину стороны АВ; 2) уравнения сторон АВ и АС в общем виде и их угловые коэффициенты; 3) угол А; 4) уравнение медианы АD; 5) уравнение высоты СЕ и ее длину.
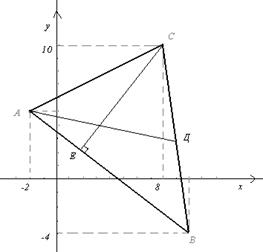
1)Расстояние между двумя точками А (х 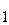 ;
; 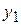 );В (х
);В (х 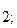 у
у 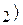 определяется по формуле d=
определяется по формуле d= 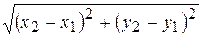 (1),
(1),
воспользовавшись которой находим длину стороны АВ: d= 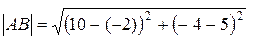 =
= 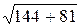 =
= 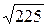 =15.
=15.
2)Уравнение прямой, проходящей через заданные точки А(х 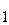 ;у
;у 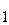 ) и В(х
) и В(х 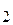 ;у
;у 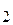 ) имеет вид:
) имеет вид: 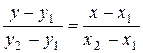 . (2)
. (2)
Подставляя в (2) координаты А и В получим уравнение прямой (АВ):
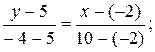
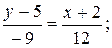
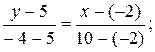
4у-20=-3х-6; 3х+4у-14=0- общее уравнение прямой (АВ).
Угловой коэффициент 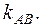 прямой АВ найдем, преобразовав полученное уравнение к виду уравнения прямой с угловым коэффициентом у=kx+b.
прямой АВ найдем, преобразовав полученное уравнение к виду уравнения прямой с угловым коэффициентом у=kx+b.
4у= -3х+14, 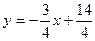 , т.е.
, т.е. 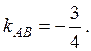
Подставляя в (2) координаты А и С получим уравнение прямой (АС):
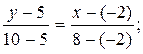
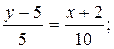 х+2=2у-10,
х+2=2у-10,
х-2у+12=0- общее уравнение прямой (АС), 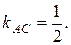
3) Требуется найти угол А между прямыми (АВ) и (АС), подставим угловые коэффициенты 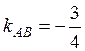 и
и 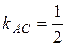 в формулу:
в формулу:
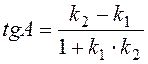 (3),
(3),
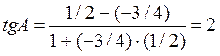 , следовательно, А=arctg2
, следовательно, А=arctg2 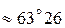
 .
.
4)AD- медиана, поэтому точка D делит отрезок ВС пополам. Для вычисления координат середины отрезка воспользуемся следующими формулами:
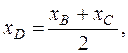
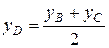 (4),
(4),
в которые подставим координаты точек В и С:
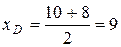 ; у
; у 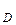 =
= 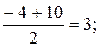 то есть D(9;3).
то есть D(9;3).
Подставив в формулу (2) координаты точек А и D получим уравнение прямой (AD)- медианы:
(AD): 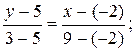 11у-55=-2х-4;
11у-55=-2х-4;
(AD): 2х+11у-51=0.
5) Высота СЕ перпендикулярна стороне АВ. Известно, что если две прямые взаимно перпендикулярны, то их угловые коэффициенты связаны соотношением: k 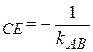 , то есть k
, то есть k 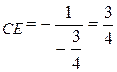 .
.
Для составления уравнения высоты CD воспользуемся уравнением прямой, проходящей через заданную точку 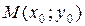 с заданным угловым коэффициентом k, которое имеет вид:
с заданным угловым коэффициентом k, которое имеет вид: 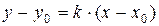 (5).
(5).
Подставив в (5) координаты точки С и угловой коэффициент k 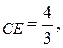 получаем
получаем
(CE): у-10= 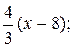 3у-30=4х-32; 4х-3у=2.
3у-30=4х-32; 4х-3у=2.
Чтобы найти длину (СЕ), определим координаты точки Е- точки пересечения высоты (СЕ) и прямой (АВ). Для этого решаем совместно систему уравнений (АВ) и (СЕ):
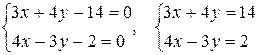 . Умножим первое уравнение на 4, а второе на- 3, получим
. Умножим первое уравнение на 4, а второе на- 3, получим 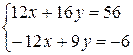 , сложив эти два уравнения, получим 25y=50, т.е. y=2. Найдём x, подставив y=2 в первое из исходных уравнений: 3x+8-14=0, откуда x=2.
, сложив эти два уравнения, получим 25y=50, т.е. y=2. Найдём x, подставив y=2 в первое из исходных уравнений: 3x+8-14=0, откуда x=2.
Следовательно, Е(2;2). Длина высоты СЕ определяется по формуле (1):
d= 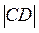 =
= 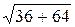 =
= 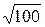 =10.
=10.
3 Найти указанные пределы:
1. 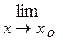
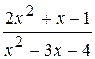


 : а) х
: а) х 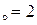 , б) х
, б) х 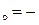 1, в) х
1, в) х 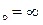 .
.
2. 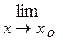
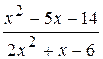


 : а) х
: а) х 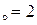 , б) х
, б) х 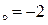 , в) х
, в) х 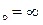 .
.
3. 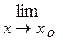
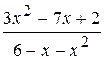

 : а) х
: а) х 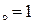 , б) х
, б) х 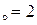 , в) х
, в) х 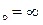 .
.
4. 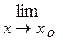
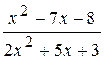 : а) х
: а) х 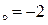 , б) х
, б) х  , в) х
, в) х 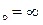 .
.
5. 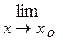
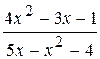 : а) х
: а) х  , б) х
, б) х 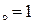 , в) х
, в) х 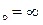 .
.
6. 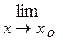
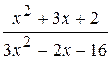 : а) х
: а) х 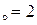 , б) х
, б) х 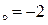 , в) х
, в) х 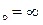 .
.
7. 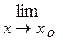
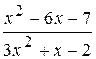 : а) х
: а) х 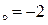 , б) х
, б) х  , в) х
, в) х 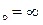 .
.
8. 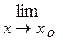
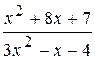 : а) х
: а) х 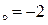 , б) х
, б) х  , в) х
, в) х 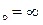 .
.
9. 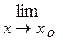
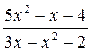 : а) х
: а) х  , б) х
, б) х 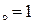 , в) х
, в) х 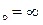 .
.
10. 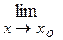
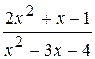 : а) х
: а) х 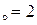 , б) х
, б) х  , в) х
, в) х 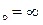 .
.
11. 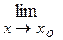
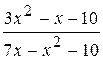 : а) х
: а) х 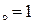 , б) х
, б) х 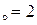 , в) х
, в) х 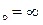 .
.
12. 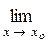
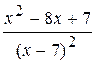 : а) х
: а) х 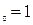 , б) х
, б) х 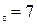 , в) х
, в) х 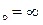 .
.
13. 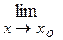
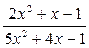 : а) х
: а) х 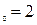 , б) х
, б) х 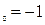 , в) х
, в) х 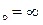 .
.
14. 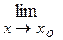
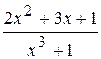 : а) х
: а) х 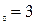 , б) х
, б) х 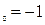 , в) х
, в) х 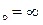 .
.
15. 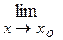
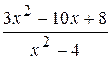 : а) х
: а) х 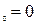 , б) х
, б) х 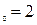 , в) х
, в) х 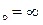 .
.
16. 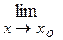
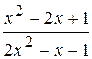 : а) х
: а) х 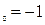 , б) х
, б) х 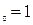 , в) х
, в) х 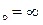 .
.
17. 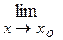
 : а) х
: а) х 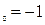 , б) х
, б) х 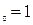 , в) х
, в) х 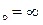 .
.
18. 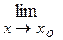
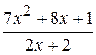 : а) х
: а) х 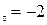 , б) х
, б) х 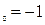 , в) х
, в) х 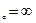 .
.
19. 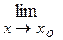
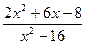 : а) х
: а) х 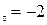 , б) х
, б) х 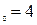 , в) х
, в) х 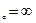 .
.
20. 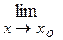
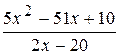 : а) х
: а) х 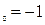 , б) х
, б) х 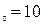 , в) х
, в) х 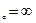 .
.
Решение типовых примеров
1) 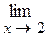
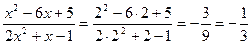 ;
;
2) 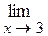

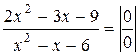 .
.
При подстановке вместо переменной x её предельного значения 3, получается неопределенность вида 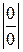 . Для избавления от этого вида неопределенности представим квадратные трехчлены числителя и знаменателя в виде произведения линейных множителей, воспользовавшись известной формулой,где
. Для избавления от этого вида неопределенности представим квадратные трехчлены числителя и знаменателя в виде произведения линейных множителей, воспользовавшись известной формулой,где 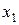 и
и 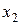 -корни квадратного трехчлена
-корни квадратного трехчлена 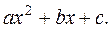
У нас 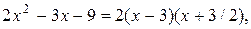 т.к. дискриминант квадратного трехчлена D=9-4
т.к. дискриминант квадратного трехчлена D=9-4 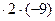 =81, а следовательно,
=81, а следовательно, 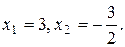
По аналогии 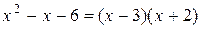 .
.
Теперь условие задачи можно переписать в другом виде и продолжить решение
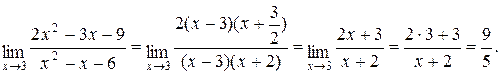
3) 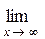
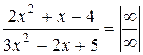 .
.
Мы получили неопределенность вида 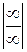 , избавиться от которой можно делением числителя и знаменателя дроби на старшую степень переменной, т.е. на
, избавиться от которой можно делением числителя и знаменателя дроби на старшую степень переменной, т.е. на 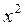 .
.
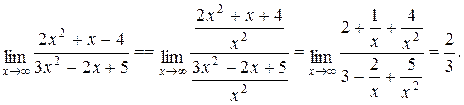
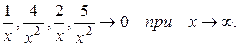 .
.
4 Найти производные заданных функций
1. а) у= 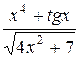 ; б) у=cos ln8x;
; б) у=cos ln8x;
2. а)у= 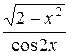 ; б) у=ln arcsin3x;
; б) у=ln arcsin3x;
3. а) у= 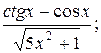 б) у=arctg ln5x;
б) у=arctg ln5x;
4. а) у= 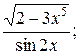 б) у=ln cos4x;
б) у=ln cos4x;
5. а) у= 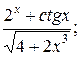 б) у=cos ln7x;
б) у=cos ln7x;
6. а) у= 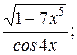 б) у= ln sin7x;
б) у= ln sin7x;
7. а) у= 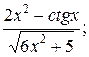 б) у=arctg ln5x;
б) у=arctg ln5x;
8. а) у= 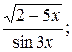 б) у=ln arcsin2x;
б) у=ln arcsin2x;
9. а) у= 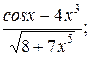 б) у=sin ln7x;
б) у=sin ln7x;
10. а) у= 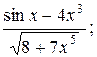 б) у=tg ln7x;
б) у=tg ln7x;
11. а) у= 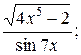 б) у=ln cos6x;
б) у=ln cos6x;
12. а) у= 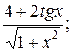 б) у=ln arctg2x;
б) у=ln arctg2x;
13. а) у= 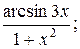 б) у=cos ln(5x+1);
б) у=cos ln(5x+1);
14. а) у= 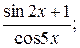 б) у=arccos ln4x;
б) у=arccos ln4x;
15. а) у= 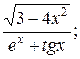 б) у=arctg ln5x;
б) у=arctg ln5x;
16. а) у= 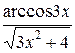 ; б) у=ln sin(6x+1);
; б) у=ln sin(6x+1);
17. а) у= 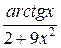 ; б) у=sin ln(1-2x);
; б) у=sin ln(1-2x);
18. а) у= 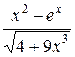 ; б) у=ln arccos5x;
; б) у=ln arccos5x;
19. а) у= 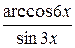 ; б) у=arcsin ln(2x-1);
; б) у=arcsin ln(2x-1);
20. а) у= 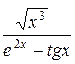 ; б) у=ln arccos7x.
; б) у=ln arccos7x.
При решении всех последующих задач кроме таблиц производных будут использованы известные правила дифференцирования суммы, разности, произведения, дроби и теорема о производной сложной функции.
1. 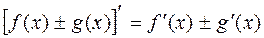 ,
,
2. 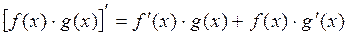 ,
,
3. 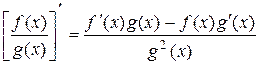 .
.
4. Если задана сложная функция y=f(u), где u=z(x), т.е. y=f(z(x)) и каждая из функций y и u дифференцируема по своему аргументу, то 
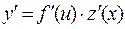 .
.
Решение типового примера
а) у= 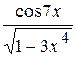 .
.
Если в знаменателе дроби стоит степень какого-либо числа, то эту дробь можно представить как отрицательную степень числа, например 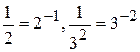 , так же
, так же 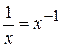 ,
, 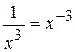 и т.д. Подкоренное выражение можно записать в виде степени, показателем которой является дробь:
и т.д. Подкоренное выражение можно записать в виде степени, показателем которой является дробь: 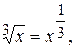
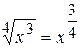 ,
, 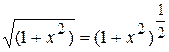 и т.д. Поэтому
и т.д. Поэтому
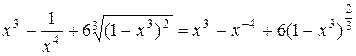 ,
,
y  =
= 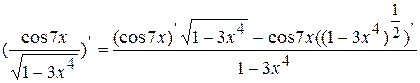 = =
= = 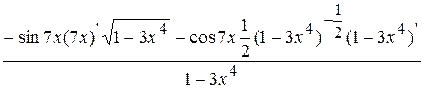 =
= 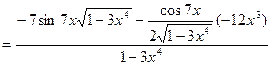 =
= 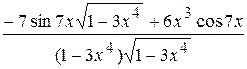 .
.
б) у=ln arcsin6x
y  = (ln arcsin6x)
= (ln arcsin6x)  =
= 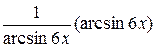
 =
=
= 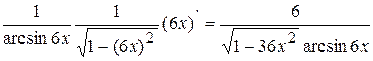 .
.
5 Исследовать данную функцию (т.е. найти точки экстремума и перегиба, интервалы возрастания, убывания, выпуклости и вогнутости графика функции) и построить ее графики.
1. y= 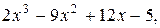
2. y= 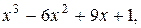
3. y= 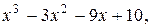
4. y= 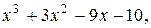
5. y= 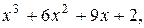
6. y= 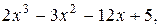
7.y= 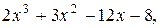
8. y= 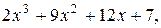
9. y= 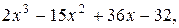
10.y= 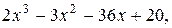
11. y= 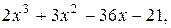
12. y= 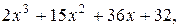
13. y= 
14. y= 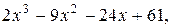
15. y= 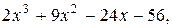
16. y= 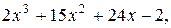
17. y= 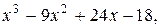
18. y= 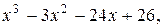
19. y= 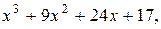
20. y= 
Решение типовой задачи
Исследовать на экстремум функцию 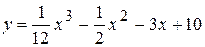 и определить интервалы ее возрастания и убывания, найти точки перегиба графика этой функции и определить интервалы выпуклости и вогнутости графика. Построить график.
и определить интервалы ее возрастания и убывания, найти точки перегиба графика этой функции и определить интервалы выпуклости и вогнутости графика. Построить график.
Решение.
Чтобы найти точки экстремума, вычисляем производную и приравниваем ее к нулю, решаем полученное уравнение:
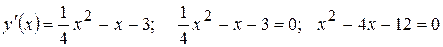
Корни уравнения 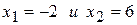 - критические точки. Эти точки разбивают числовую ось на три интервала:
- критические точки. Эти точки разбивают числовую ось на три интервала: 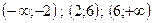 .
.
Производную 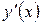 можно представить так:
можно представить так:  .
.
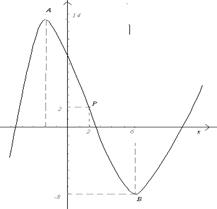 Из последнего равенства видно, что в первом интервале
Из последнего равенства видно, что в первом интервале 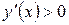 , во втором
, во втором 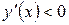 и в третьем интервале
и в третьем интервале 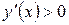 . Следовательно, в первом и третьем интервалах функция возрастает, а во втором убывает. Так как в критической точке
. Следовательно, в первом и третьем интервалах функция возрастает, а во втором убывает. Так как в критической точке 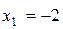 производная меняет знак с плюса на минус, то в этой точке функция имеет максимум. А в силу того, что в точке
производная меняет знак с плюса на минус, то в этой точке функция имеет максимум. А в силу того, что в точке 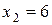 производная меняет знак с минуса на плюс, функция имеет минимум в этой точке. Вычислим значение функции в этих точках:
производная меняет знак с минуса на плюс, функция имеет минимум в этой точке. Вычислим значение функции в этих точках: 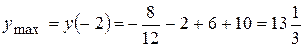 .
. 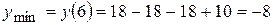
Точка B(6;-8)- точка минимума.
Точка A(-2;13 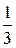 )- точка максимума.
)- точка максимума.
Чтобы найти точки перегиба, интервалы выпуклости и вогнутости, находим вторую производную, приравниваем ее нулю и решаем полученное уравнение.
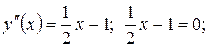
x-2=0; x=2 – критическая точка второго рода. Эта точка разбивает числовую ось на два интервала: 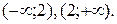
 Как видно, в первом случае
Как видно, в первом случае 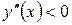 , во втором -
, во втором - 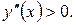 Следовательно, в первом интервале график функции – выпуклый, во втором – вогнутый. Так как производная
Следовательно, в первом интервале график функции – выпуклый, во втором – вогнутый. Так как производная 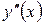 при переходе через точку х=2 меняет свой знак, то х=2 есть абсцисса точки перегиба графика. Вычисляем ординату этой точки:
при переходе через точку х=2 меняет свой знак, то х=2 есть абсцисса точки перегиба графика. Вычисляем ординату этой точки:
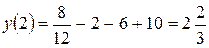 ;
;
Таким образом, точка 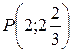 – точка перегиба графика функции.
– точка перегиба графика функции.
По результатам исследования строим график.
6 В задачах 1-20 требуется найти указанные неопределенные интегралы:
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
Date: 2015-06-06; view: 557; Нарушение авторских прав