
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Равенство Клаузиуса
|
|
Пусть круговой процесс, совершаемый системой, – квазистатический. Для него справедливо неравенство Клаузиуса
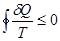 .
.
Под температурой 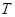 для такого процесса мы можем понимать температуру самой системы, поскольку температуры системы и среды одинаковы.
для такого процесса мы можем понимать температуру самой системы, поскольку температуры системы и среды одинаковы.
Т.к. квазистатический процесс обратим в узком смысле, то мы можем провести тот же процесс по тому же пути, но в противоположном направлении.
Для обратного процесса также справедливо неравенство Клаузиуса
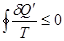 . (!.23)
. (!.23)
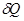 и
и 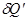 обозначают элементарные количества теплоты, получаемые системой на отдельных участках прямого и обратного процессов, соответственно. Поскольку система проходит в обоих случаях через одни и те же равновесные состояния, то
обозначают элементарные количества теплоты, получаемые системой на отдельных участках прямого и обратного процессов, соответственно. Поскольку система проходит в обоих случаях через одни и те же равновесные состояния, то 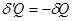 , и выражение (!.23) приводится к виду:
, и выражение (!.23) приводится к виду:
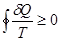 . (!.24)
. (!.24)
Выражения (!.22) и (!.24) совместимы только в том случае, если взят знак равенства.
Т.о., для квазистатического процесса неравенство Клаузиуса переходит в равенство:
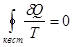 . (!.25)
. (!.25)
Энтропия.
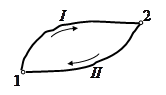 Допустим, что система может переходить из начального состояния 1 в конечное состояние 2 несколькими путями, причем каждый из них представляет собой квазистатический процесс.
Допустим, что система может переходить из начального состояния 1 в конечное состояние 2 несколькими путями, причем каждый из них представляет собой квазистатический процесс.
Рассмотрим два из них – 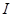 и
и 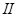 . Объединим эти процессы в один
. Объединим эти процессы в один
квазистатический круговой процесс 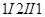 и применим к нему равенство
и применим к нему равенство
Клаузиуса:
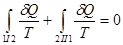 , или
, или 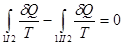 .
.
Т.о,
 . (!.26).
. (!.26).
Отношение количества теплоты, полученного системой при данной температуре, к значению 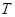 этой температуры называется приведенным количеством теплоты. Тогда величина
этой температуры называется приведенным количеством теплоты. Тогда величина 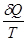 есть элементарное приведенное количество теплоты, полученное в бесконечно малом процессе, а интеграл
есть элементарное приведенное количество теплоты, полученное в бесконечно малом процессе, а интеграл 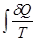 - приведенное количество теплоты, полученное системой в конечном процессе.
- приведенное количество теплоты, полученное системой в конечном процессе.
Пояснить физический смысл понятия «приведенное количество теплоты» можно, рассматривая передачу одного и того же количества теплоты при разных температурах. Тепло, переданное газу и вызвавшее повышение его температуры, например от 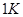 до
до 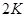 , приведет к весьма заметной активизации беспорядочного теплового движения молекул газа, в то время как количество теплоты, вызвавшее повышение температуры газа от
, приведет к весьма заметной активизации беспорядочного теплового движения молекул газа, в то время как количество теплоты, вызвавшее повышение температуры газа от 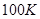 до
до 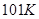 , практически не окажет влияния на тепловое движение молекул. Т.о., приведенное количество теплоты показывает «ценность» полученного тепла, учитывая температуру системы, при которой оно было получено.
, практически не окажет влияния на тепловое движение молекул. Т.о., приведенное количество теплоты показывает «ценность» полученного тепла, учитывая температуру системы, при которой оно было получено.
Используя такую терминологию, равенству Клаузиуса (!.26) можно дать следующее определение.
Приведенное количество теплоты, полученное системой при любом квазистатическом круговом процессе, равно нулю.
Или эквивалентное ему.
Приведенное количество теплоты, квазистатически полученное системой, не зависит от пути перехода, а определяется лишь начальным и конечным состояниями системы.
Мы получили весьма важный результат. Равенство Клаузиуса, интерпретированное таким образом, позволяет ввести новую функцию состояния, которая получила название «энтропия» (от греческого entropia – поворот, превращение).
Энтропия системы есть функция её состояния, определенная с точностью до произвольной постоянной.
Разность энтропий системы в двух равновесных состояниях 2 и 1, по определению, равна приведенному количеству теплоты, которое надо сообщить системе, чтобы перевести её из состояния 1 в состояние 2 по любому квазистатическому пути.
Обозначив энтропии системы в состояниях 1 и 2 через 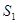 и
и 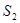 , по определению, можем записать
, по определению, можем записать
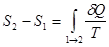 . (!.27)
. (!.27)
С произвольной постоянной при определении энтропии дело обстоит так же, как и при определении энергии системы. Физический смысл имеет не сама энтропия, а разность энтропий в рассматриваемых состояниях. При необходимости за нуль можно принять значение энтропии в каком-либо определенном состоянии. Тогда постоянной в определении энтропии можно придать определенное значение.
Итак,
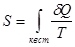 , (!.28)
, (!.28)
где интеграл берется для произвольного квазистатического процесса, переводящего систему в рассматриваемое состояние из другого состояния, условно принятого за начальное.
Для дифференциала функции 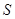 имеем
имеем
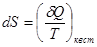 . (!.29)
. (!.29)
Уже неоднократно отмечалось, что 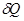 не является дифференциалом функции. В то же время формула (!.29) показывает, что если
не является дифференциалом функции. В то же время формула (!.29) показывает, что если 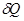 есть элементарное количество теплоты, квазистатически полученное системой при температуре
есть элементарное количество теплоты, квазистатически полученное системой при температуре 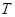 , то после деления на
, то после деления на 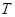 оно переходит в полный дифференциал функции состояния – энтропии.
оно переходит в полный дифференциал функции состояния – энтропии.
В качестве примера нахождения вновь введенной функции состояния вычислим энтропию 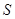 одного моля идеального газа. Для всякого квазистатического процесса, в котором газу передается бесконечно малое количество теплоты
одного моля идеального газа. Для всякого квазистатического процесса, в котором газу передается бесконечно малое количество теплоты 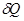 , можем написать
, можем написать
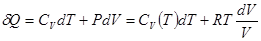 .
.
Отсюда
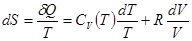 ,
,
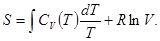
Если теплоемкость 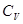 не зависит от температуры, то интеграл легко берется, и мы получаем
не зависит от температуры, то интеграл легко берется, и мы получаем
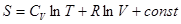 . (!.30)
. (!.30)
Для 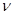 молей газа
молей газа
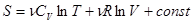 . (!.31)
. (!.31)
из сравнения выражений (!.30) и (!.31) следует, что аддитивная постоянная может зависеть от числа частиц в газе. Эту постоянную следует определить так, чтобы энтропия 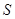 была пропорциональна числу частиц в газе (числу молей газа).
была пропорциональна числу частиц в газе (числу молей газа).
Тогда выражение (!.31) примет вид
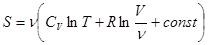 , (!.32)
, (!.32)
или
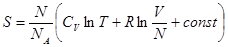 . (!.33)
. (!.33)
В двух последних выражениях аддитивная постоянная не зависит от числа частиц. Поэтому формулы (!.32) и (!.33) применимы к идеальным газам как с постоянным, так и с переменным числом частиц.
Если рассматриваемый квазистатический процесс – адиабатический, то теплообмен отсутствует (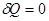 ) и, следовательно,
) и, следовательно, 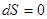 , а энтропия системы
, а энтропия системы 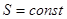 . Т.о.. всякий квазистатический адиабатический процесс есть процесс, происходящий без изменения энтропии. Поэтому его также называют изоэнтропическим процессом.
. Т.о.. всякий квазистатический адиабатический процесс есть процесс, происходящий без изменения энтропии. Поэтому его также называют изоэнтропическим процессом.
Закон возрастания энтропии.
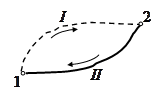 |
Пусть термодинамическая система по пути 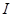 переходит из равновесного
переходит из равновесного
состояния 1 в равновесное состояние 2, причем процесс перехода является 
необратимым.
Напомним, что необратимым называется процесс, после совершения
которого возврат системы в исходное состояние неизбежно связан с
изменениями в окружающих телах (среде).
Вернем систему из состояния 2 в состояние 1 квазистатически по какому-либо пути 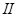 .
.
На всем пути неравенство Клаузиуса можно написать в следующем виде
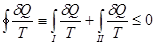 . (!.34)
. (!.34)
Поскольку процесс 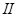 квазистатический, для которого выполняется равенство Клаузиуса, то
квазистатический, для которого выполняется равенство Клаузиуса, то
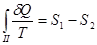 . (!.35)
. (!.35)
Тогда неравенство Клаузиуса (!.34) принимает вид
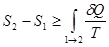 . (!.36)
. (!.36)
Здесь под температурой 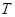 следует понимать температуру окружающей среды, при которой среда отдает системе количество теплоты
следует понимать температуру окружающей среды, при которой среда отдает системе количество теплоты 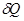 .
.
Пусть система адиабатически изолирована, тогда 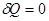 и
и 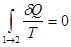 . Отсюда получаем
. Отсюда получаем
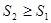 . (!.37)
. (!.37)
Полученное соотношение выражает закон возрастания энтропии:
Энтропия адиабатически изолированной системы не может убывать: она либо возрастает (в неравновесных процессах), либо остается постоянной (при квазистатических процессах).
Если для состояний 1 и 2 адиабатически изолированной системы определено, что 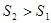 , то её переход из состояния (1) с меньшей энтропией в состояние (2) с большей энтропией не противоречит постулату второго начала термодинамики и в этом смысле возможен. Напротив, самопроизвольный переход рассматриваемой системы из состояния 2 в состояние 1 невозможен, т.к. он сопровождался бы убыванием энтропии. Обобщая сказанное, можно заключить, что самопроизвольно протекающие в природе процессы сопровождаются возрастанием энтропии.
, то её переход из состояния (1) с меньшей энтропией в состояние (2) с большей энтропией не противоречит постулату второго начала термодинамики и в этом смысле возможен. Напротив, самопроизвольный переход рассматриваемой системы из состояния 2 в состояние 1 невозможен, т.к. он сопровождался бы убыванием энтропии. Обобщая сказанное, можно заключить, что самопроизвольно протекающие в природе процессы сопровождаются возрастанием энтропии.
Т.о., второе начало термодинамики позволяет судить о направлении процессов, которые могут происходить в природе.
Чтобы проиллюстрировать это утверждение, рассмотрим, например, адиабатическое расширение газа в пустоту.


 Пусть газ изначально занимает одну из частей цилиндра с жесткими адиабатическими стенками, объемом
Пусть газ изначально занимает одну из частей цилиндра с жесткими адиабатическими стенками, объемом
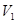 , а во второй части цилиндра, отделенной перегородкой и имеющей объем
, а во второй части цилиндра, отделенной перегородкой и имеющей объем
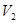 – вакуум. Затем перегородка убирается, и газ расширяется в пустоту.
– вакуум. Затем перегородка убирается, и газ расширяется в пустоту.
Процесс прекращается, когда выравниваются давление и температура во всем
объеме цилиндра.
В результате прошедшего в жесткой адиабатической оболочке процесса (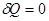 и
и 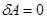 , т.к. работа против вакуума не совершается) внутренняя энергия газа не изменяется. Поскольку газ идеальный, то не изменится и его температура (
, т.к. работа против вакуума не совершается) внутренняя энергия газа не изменяется. Поскольку газ идеальный, то не изменится и его температура (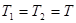 ), которая однозначно определяется внутренней энергией газа. Начальное и конечное состояния газа равновесны, но является ли рассматриваемый процесс обратимым?
), которая однозначно определяется внутренней энергией газа. Начальное и конечное состояния газа равновесны, но является ли рассматриваемый процесс обратимым?
Для ответа на этот вопрос следует вычислить изменение энтропии газа.
Вычислить изменение энтропии газа мы можем только переводя систему из начального состояния в конечное квазистатически, поскольку только для такого процесса имеет место равенство Клаузиуса. С другой стороны, поскольку энтропия является функцией состояния системы, то её изменение зависит только начального и конечного состояний и не зависит от пути перехода. т.е. интеграл (3.35) должен быть взят для произвольного, но обязательно квазистатического процесса, переводящего систему из начального состояния в конечное.
Квазистатически система может быть переведена в интересующее нас состояние по изотерме. Для осуществления этого процесса необходимо отказаться от теплоизолирующей и жесткой оболочки, поскольку для совершения работы и поддержания в течение всего процесса температуры газа постоянной и равной 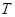 , среда должна поставлять газу потребное количество теплоты.
, среда должна поставлять газу потребное количество теплоты.
Бесконечно медленно уменьшая давление на газ, изотермически переводим его из начального состояния с объемом 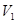 в конечное состояние с объемом
в конечное состояние с объемом 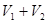 . Т.к. для изотермического процесса с идеальным газом имеем
. Т.к. для изотермического процесса с идеальным газом имеем 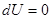 , то
, то 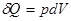 . Поэтому заимствованную из среды теплоту газ будет превращать в эквивалентную работу.
. Поэтому заимствованную из среды теплоту газ будет превращать в эквивалентную работу.
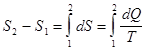 .
.
Воспользовавшись уравнением состояния идеального газа 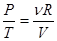 , получаем
, получаем
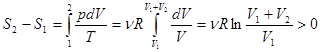 .
.
Т.о., энтропия системы возросла, следовательно, процесс адиабатического распространения газа на весь сосуд является необратимым процессом, т.е. он не может быть проведен в обратном направлении без каких-либо изменений в окружающей среде.
Однако, в процессе адиабатического расширения газа, в отличие от выбранного для вычисления изотермического, изменение энтропии системы не может быть связано с получением тепла извне.
Возникает кажущееся противоречие. Действительно, при адиабатическом расширении газа теплота к системе не подводилась, т.е. 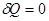 . Поэтому из равенства напрашивается очевидный вывод:
. Поэтому из равенства напрашивается очевидный вывод:
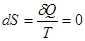 и, следовательно,
и, следовательно, 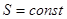 ,
,
т.е. энтропия системы в начальном и конечном состояниях должна быть одной и той же.
Ошибка такого рассуждения заключена в неправомерности применения равенства 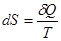 , относящегося только к квазиравновесным процессам, к неравновесному процессу случае адиабатического расширения газа в пустоту.
, относящегося только к квазиравновесным процессам, к неравновесному процессу случае адиабатического расширения газа в пустоту.
Еще раз подчеркнем, что знак равенства в выражении
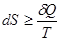 , (!.38) относится только к равновесным процессам, а неравенство справедливо для любого необратимого процесса, в ходе которого равновесие в системе нарушается, что и имеет место в рассматриваемом нами случае адиабатического расширения газа.
, (!.38) относится только к равновесным процессам, а неравенство справедливо для любого необратимого процесса, в ходе которого равновесие в системе нарушается, что и имеет место в рассматриваемом нами случае адиабатического расширения газа.
Различные самопроизвольно протекающие в природе процессы сопровождаются возрастанием энтропии.
Заключая сказанное, отметим, что в термодинамике энтропия вводится для определения меры необратимого рассеяния энергии.
Обобщение понятия энтропии на неравновесные состояния.
Введенное выше понятие энтропии относится только к равновесным состояниям. Рассмотрим теперь систему, находящуюся в неравновесном состоянии, предполагая, что такая система может быть мысленно разбита на отдельные макроскопические подсистемы, каждая из которых практически находится в равновесии. Вообще говоря, созданные нашим воображением подсистемы могут совершать макроскопические движения. Параметры, характеризующие внутреннее состояние подсистем (например, температура 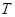 и давление
и давление 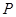 ) и их макроскопическое движение, могут плавно меняться от подсистемы к подсистеме. В этом случае говорят, что имеет место локальное термодинамическое равновесие. Тогда можно говорить об энтропии
) и их макроскопическое движение, могут плавно меняться от подсистемы к подсистеме. В этом случае говорят, что имеет место локальное термодинамическое равновесие. Тогда можно говорить об энтропии 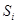 каждой из подсистем в том смысле, в котором это понятие было нами введено. А энтропию всей систему можно определить как сумму энтропий таких подсистем:
каждой из подсистем в том смысле, в котором это понятие было нами введено. А энтропию всей систему можно определить как сумму энтропий таких подсистем:
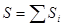 . (!.39) Подчеркнем, что макроскопические подсистемы, на которые мысленно разбивается система, должны выбираться, когда это возможно, настолько малыми, чтобы сумма (!.39) не изменялась при дальнейшем дроблении системы. Введенное здесь расширенное понятие энтропии мы относим лишь к тем случаям, когда это сделать можно.
. (!.39) Подчеркнем, что макроскопические подсистемы, на которые мысленно разбивается система, должны выбираться, когда это возможно, настолько малыми, чтобы сумма (!.39) не изменялась при дальнейшем дроблении системы. Введенное здесь расширенное понятие энтропии мы относим лишь к тем случаям, когда это сделать можно.
Не проводя доказательства, отметим, что при таком обобщенном понимании энтропии теорема о её возрастании остается в силе. (Доказательство в «Сивухин, т.II, с. 140-142»).
Если состояние системы таково, что её нельзя разбить на макроскопические части, находящиеся в локальном термодинамическом равновесии, то приведенное обобщение понятия энтропии теряет смысл. Однако статистическая физика позволяет распространить понятие энтропии и закон её возрастания и на такие состояния.
Термодинамические функции.
При описании состояний термодинамических систем наряду с энтропией можно пользоваться множеством других, связанных с ней функций состояния. Однако среди этого многообразия существуют функции, имеющие наиболее важное значение в термодинамике. Рассмотрим эти функции и установим их связь с энтропией применительно к различным процессам, в которых участвует система.
Пусть процессы, в которых участвует система, квазиравновесные. Для таких процессов 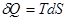 и уравнение первого начала термодинамики
и уравнение первого начала термодинамики
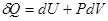 (!.40)
(!.40)
может быть представлено в виде
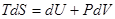 . (!.41)
. (!.41)
Используя введенную ранее энтальпию 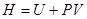 и
и 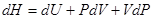 , исключаем
, исключаем 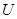 и получаем
и получаем
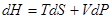 . (!.42)
. (!.42)
Поскольку 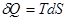 , то при постоянном давлении (
, то при постоянном давлении (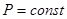 ,
, 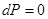 ) получаем
) получаем
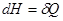 . (!.43)
. (!.43)
Именно в силу этого равенства этальпию называют тепловой функцией или теплосодержанием.
Энтальпия 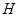 есть такая функция состояния, приращение которой в квазистатическом процессе, проводимом при постоянном давлении, определяет количество теплоты, полученное системой.
есть такая функция состояния, приращение которой в квазистатическом процессе, проводимом при постоянном давлении, определяет количество теплоты, полученное системой.
Рассмотрим теперь функции состояния, играющие особенно важную роль в термодинамике. Это введенная Гельмгольцем свободная энергия 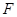 и термодинамический потенциал
и термодинамический потенциал 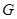 , введенный Гиббсом.
, введенный Гиббсом.
Эти функции состояния определяются выражениями
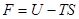 (!.44)
(!.44)
и
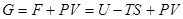 . (!.45)
. (!.45)
Дифференциалы этих функций найдем, выразив предварительно из (!.41) дифференциал внутренней энергии
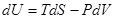 . (!.46)
. (!.46)
Тогда
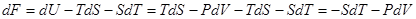 ,
,
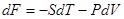 , (!.47)
, (!.47)
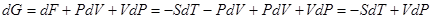 .
.
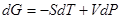 . (!.48)
. (!.48)
При изотермическом процессе (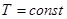 ,
, 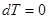 ):
): 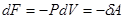 , поэтому
, поэтому
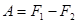 . (!.49)
. (!.49)
Т.о., функция состояния 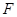 может быть интерпретирована следующим образом:
может быть интерпретирована следующим образом:
Свободная энергия 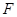 есть функция состояния системы, убыль которой в квазистатическом процессе, проводимом при постоянной температуре, определяет работу, произведенную системой.
есть функция состояния системы, убыль которой в квазистатическом процессе, проводимом при постоянной температуре, определяет работу, произведенную системой.
Величина 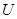 есть внутренняя, или полная энергия системы, но если система находится в тепловом контакте со средой, температура
есть внутренняя, или полная энергия системы, но если система находится в тепловом контакте со средой, температура 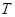 которой поддерживается постоянной, то только часть этой энергии, а именно
которой поддерживается постоянной, то только часть этой энергии, а именно 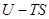 , может быть использована для получения работы. По-видимому, Гельмгольц как раз этот смысл и вкладывал в термин «свободная энергия». Оставшаяся часть внутренней энергии системы при таких условиях не может быть превращена в работу. Она называется связанной энергией.
, может быть использована для получения работы. По-видимому, Гельмгольц как раз этот смысл и вкладывал в термин «свободная энергия». Оставшаяся часть внутренней энергии системы при таких условиях не может быть превращена в работу. Она называется связанной энергией.
Согласно неравенству Клаузиуса, имеем
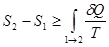 ,
,
если температура в процессе теплообмена поддерживается постоянной (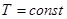 ), то
), то
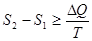 .
.
В соответствии с первым началом (37)
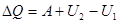 ,
,
тогда
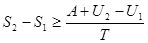 , или
, или  , откуда
, откуда 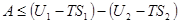 .
.
Т.о.,
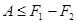 , (!.50)
, (!.50)
где, как и прежде, знак равенства относится к обратимым процессам. Для неравновесных процессов имеем
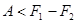 .
.
Наконец, отметим, что для лишь в предельном случае при  различие между внутренней и свободной энергиями пропадает.
различие между внутренней и свободной энергиями пропадает.
Перейдем теперь к обсуждению термодинамического потенциала Гиббса 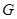 . В термодинамике, наряду с полной работой, совершаемой системой, рассматривают, так называемую, полезную работу. Понятие полезной работы вводится для системы, помещенной в находящуюся в равновесии среду, температура
. В термодинамике, наряду с полной работой, совершаемой системой, рассматривают, так называемую, полезную работу. Понятие полезной работы вводится для системы, помещенной в находящуюся в равновесии среду, температура 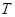 и давление
и давление 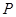 которой поддерживаются постоянными. Если система может совершать работу не только против давления среды, но и над другими телами, то эту, последнюю, составляющую работы и называют полезной работой
которой поддерживаются постоянными. Если система может совершать работу не только против давления среды, но и над другими телами, то эту, последнюю, составляющую работы и называют полезной работой 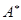 .
.
Работа, производимая против давления среды, определяется выражением 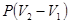 . Вычитая эту составляющую из полной работы
. Вычитая эту составляющую из полной работы 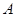 , для полезной работы
, для полезной работы 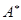 из (!.50) получаем
из (!.50) получаем
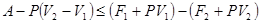 ,
,
или
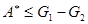 . (!.51)
. (!.51)
Здесь опять равенство выполняется для равновесных процессов, а неравенство имеет место для процессов неравновесных.
Когда термодинамическая система состоит только из твердых и жидких тел, изменением её объема при всех процессах можно, как правило, пренебречь. В этих случаях различие между полной работой 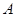 и полезной работой системы
и полезной работой системы 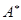 исчезает. Напротив, для газообразных систем это различие может быть существенным.
исчезает. Напротив, для газообразных систем это различие может быть существенным.
Уравнения (!.42), (!.46), (!.47) и (!.48) позволяют рассматривать внутреннюю энергию, энтальпию, свободную энергию и термодинамический потенциал как функции соответствующих пар аргументов:
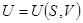 ;
; 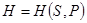 ;
;
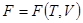 ;
; 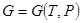 . (!.52)
. (!.52)
Такие соотношения называются каноническими уравнениями состояния вещества. Их ввел в термодинамику Гиббс, который отметил, что каждое из канонических уравнений состояния дает о свойствах вещества более богатую информацию, чем в отдельности термическое или калорическое уравнения состояния в отдельности. Иначе, каноническое уравнение состояния, в какой бы из четырех форм (!.52) оно ни было взято, содержит полные сведения о термических и калорических свойствах вещества.
Зная термодинамические функции (потенциалы), можно получить дифференцированием этих потенциалов все остальные параметры, характеризующие систему, подобно тому как в механике можно определить компоненты действующих на систему сил, дифференцируя потенциальную энергию системы по соответствующим координатам.
При помощи термодинамических потенциалов выражаются условия термодинамического равновесия системы и критерии его устойчивости.
Для полных изменений функций состояния системы из (!.51) получаем
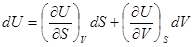 ;
; 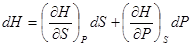 ;
;
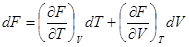 ;
; 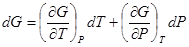 . (!.53)
. (!.53)
Сравнивая соотношения (!.53) с (!.42), (!.46), (!.47) и (!.48), получаем
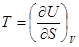 ,
, 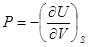 ; (!.54)
; (!.54)
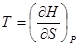 ,
, 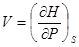 ; (!.55)
; (!.55)
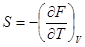 ,
, 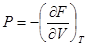 ; (!.56)
; (!.56)
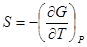 ,
, 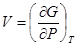 . (!.57)
. (!.57)
Из определения функций состояния 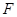 и
и 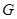 следует
следует
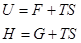 ,
,
подставив сюда выражения для энтропии из (!.56) и (!.57), получим уравнения Гиббса-Гельмгольца
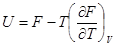 , (!.58)
, (!.58)
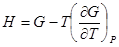 . (!.59)
. (!.59)
Проиллюстрируем примером практическую пользу, которую можно извлечь из этих уравнений.
Свободную энергию 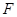 системы с точностью до слагаемого, зависящего от температуры, достаточно просто найти, вычислив работу, совершаемую системой в изотермическом процессе. Тогда по формуле (!.58) с той же точностью определяется внутренняя энергия
системы с точностью до слагаемого, зависящего от температуры, достаточно просто найти, вычислив работу, совершаемую системой в изотермическом процессе. Тогда по формуле (!.58) с той же точностью определяется внутренняя энергия 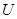 системы.
системы.
Если внутренняя энергия задана как функция двух переменных 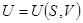 , то, продифференцировав её по
, то, продифференцировав её по 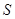 и
и 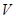 , мы найдем температуру и давление системы, т.е. получим полную информацию о её термических свойствах. Затем, воспользовавшись уравнением первого начала термодинамики (!.40), можем найти
, мы найдем температуру и давление системы, т.е. получим полную информацию о её термических свойствах. Затем, воспользовавшись уравнением первого начала термодинамики (!.40), можем найти 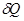 и определить соответствующие теплоемкости, получив, таким образом, полные сведения и о калорических свойствах системы.
и определить соответствующие теплоемкости, получив, таким образом, полные сведения и о калорических свойствах системы.
Ту же информацию можно получить и из трех других канонических уравнений состояния.
Если число частиц 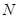 в системе может изменяться, то для описания такой системы в выражение (!.46) следует добавить член
в системе может изменяться, то для описания такой системы в выражение (!.46) следует добавить член 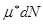 , учитывающий изменение её внутренней энергии за счет изменения числа частиц. Тогда вместо (!.46) следует писать
, учитывающий изменение её внутренней энергии за счет изменения числа частиц. Тогда вместо (!.46) следует писать
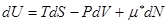 . (!.60)
. (!.60)
Таким же образом изменяться правые части выражений (!.42), (!.47) и (!.48), которые для систем с переменным числом частиц записываются в виде
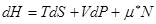 . (!.61)
. (!.61)
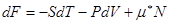 , (!.62)
, (!.62)
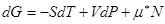 . (!.63)
. (!.63)
Величина 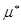 в термодинамике называется химическим потенциалом.
в термодинамике называется химическим потенциалом.
Из приведенных выражений химический потенциал может быть определен следующим образом
 . (!.64)
. (!.64)
Для толкования химического потенциала 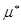 рассмотрим зависимость от числа частиц термодинамического потенциала
рассмотрим зависимость от числа частиц термодинамического потенциала 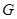 . Для систем с переменным числом частиц
. Для систем с переменным числом частиц 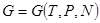 . Увеличим число частиц в системе в
. Увеличим число частиц в системе в 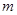 раз, сохраняя постоянными значения переменных
раз, сохраняя постоянными значения переменных 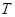 и
и 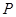 . Тогда функция
. Тогда функция 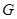 возрастет в такое же число раз, т.е.
возрастет в такое же число раз, т.е.  . Выберем теперь
. Выберем теперь 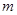 таким, чтобы
таким, чтобы 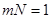 , или
, или 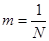 , тогда
, тогда 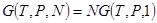 . Отсюда
. Отсюда
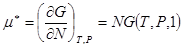 ,
,
или, с учетом предыдущего уравнения
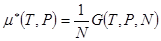 . (!.65)
. (!.65)
Т.о., химический потенциал 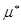 может быть истолкован как термодинамический потенциал, отнесенный к одной частице.
может быть истолкован как термодинамический потенциал, отнесенный к одной частице.
Заметим, что термодинамическое определение 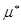 не однозначно. Для однозначности определения надо фиксировать начала отсчета внутренней энергии и энтропии.
не однозначно. Для однозначности определения надо фиксировать начала отсчета внутренней энергии и энтропии.
Интенсивные и экстенсивные параметры.
Все термодинамические величины можно разделить на две группы – интенсивные и экстенсивные.
Интенсивными называются величины, зависящие только от внутреннего состояния тел, но не зависящие от их размеров.
Параметры, пропорциональные размерам тел при их неизменном внутреннем состоянии, называются экстенсивными.
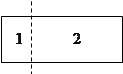 Мысленно разделим находящуюся в равновесии однородную
Мысленно разделим находящуюся в равновесии однородную
макроскопическую систему на две части. Предположим, что макроскопический
параметр 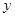 , характеризующий систему в целом, принимает для подсистем
, характеризующий систему в целом, принимает для подсистем
1 и 2 значения 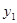 и
и 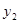 , соответственно. Тогда
, соответственно. Тогда
1) параметр 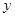 называется интенсивным, если
называется интенсивным, если
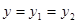 .
.
Такими параметрами являются, например, давление 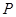 , т.к. в обеих частях системы давление то же, что и в системе в целом, и температура
, т.к. в обеих частях системы давление то же, что и в системе в целом, и температура 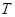 .
.
2) параметр 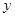 называется экстенсивным, если
называется экстенсивным, если
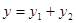 .
.
Экстенсивными параметрами являются объем 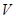 системы и её масса
системы и её масса 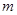 , хотя плотность
, хотя плотность 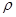 вещества в системе представляет собой интенсивный параметр. Экстенсивными величинами являются внутренняя и свободная энергия, энтропия, термодинамический потенциал и др.
вещества в системе представляет собой интенсивный параметр. Экстенсивными величинами являются внутренняя и свободная энергия, энтропия, термодинамический потенциал и др.
Термодинамическое равновесие.
Под термодинамическим равновесием понимается состояние термодинамической системы, в которое она самопроизвольно приходит через достаточно большой промежуток времени в условиях изоляции от окружающей среды. В механике для характеристики состояния равновесия мы вводили критерий устойчивости равновесия.
Достаточные условия термодинамического равновесия (условия устойчивости) могут быть получены из второго начала термодинамики. В общем случае состояние системы определяется как состояние термодинамического равновесия, когда термодинамический потенциал системы, соответствующий независимым в данных условиях переменным, минимален, а энтропия максимальна.
Рассмотрим случаи, когда на поведение системы накладываются конкретные ограничения.
Адиабатически изолируем систему от окружающей среды (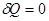 ). Пусть эта система находится в термодинамическом равновесии, причем её энтропия
). Пусть эта система находится в термодинамическом равновесии, причем её энтропия 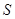 в этом состоянии максимальна, т.е. имеет большее значение, чем энтропия
в этом состоянии максимальна, т.е. имеет большее значение, чем энтропия 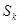 в любом бесконечно близком состоянии (
в любом бесконечно близком состоянии (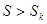 ), в которое система может перейти без отвода или подвода тепла. В таком случае на основании закона возрастания энтропии можно утверждать, что самопроизвольный адиабатический переход системы во все эти состояния невозможен, т.е. система находится в состоянии устойчивого термодинамического равновесия. Т.о., мы приходим к следующему критерию термодинамической устойчивости.
), в которое система может перейти без отвода или подвода тепла. В таком случае на основании закона возрастания энтропии можно утверждать, что самопроизвольный адиабатический переход системы во все эти состояния невозможен, т.е. система находится в состоянии устойчивого термодинамического равновесия. Т.о., мы приходим к следующему критерию термодинамической устойчивости.
Если система адиабатически изолирована и её энтропия в некотором равновесном состоянии максимальна, то это состояние термодинамически устойчиво.
Однако в задачах термодинамики часто бывает удобно вместо адиабатической изоляции системы накладывать на нее поведение другие ограничения. В таких случаях изменяются и критерии термодинамической устойчивости.
Пусть система, помещенная в среду, температура которой поддерживается постоянной и равной температуре 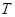 системы, заключена в жесткую оболочку (
системы, заключена в жесткую оболочку (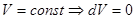 ). Поскольку работа такой системы всегда равна нулю, то из (!.50) следует
). Поскольку работа такой системы всегда равна нулю, то из (!.50) следует
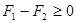 , или
, или 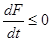 .
.
Эти неравенства означают, что необратимые процессы, происходящие при постоянных температуре (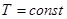 ) и объеме (
) и объеме (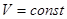 ) и приближающие систему к состоянию равновесия, сопровождаются уменьшением свободной энергии
) и приближающие систему к состоянию равновесия, сопровождаются уменьшением свободной энергии 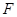 системы.
системы.
Отсюда заключаем, что если температура 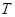 и объем
и объем 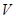 системы поддерживаются постоянными и её свободная энергия
системы поддерживаются постоянными и её свободная энергия 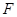 в некотором состоянии минимальна, то это состояние термодинамически устойчиво.
в некотором состоянии минимальна, то это состояние термодинамически устойчиво.
Теперь пусть система со всех сторон окружена средой, температура и давление которой поддерживаются постоянными и равными температуре 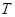 и давлению
и давлению 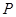 в системе. В этом случае работа может совершаться системой только против внешнего давления среды и, как следствие, полезная работа системы равна нулю (
в системе. В этом случае работа может совершаться системой только против внешнего давления среды и, как следствие, полезная работа системы равна нулю (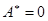 ). Тогда из (!.51) следует, что
). Тогда из (!.51) следует, что
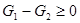 , или
, или 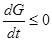 .
.
Т.о., любые процессы, протекающие в системе при постоянных температуре 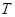 и давлении
и давлении 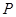 и приближающие её к состоянию равновесия, сопровождаются уменьшением термодинамического потенциала системы.
и приближающие её к состоянию равновесия, сопровождаются уменьшением термодинамического потенциала системы.
Отсюда вытекает, что если температура 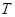 и давление
и давление 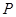 системы поддерживаются постоянными и её термодинамический потенциал
системы поддерживаются постоянными и её термодинамический потенциал 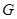 в некотором состоянии минимален, то это состояние термодинамически устойчиво.
в некотором состоянии минимален, то это состояние термодинамически устойчиво.
Рассмотрим еще два случая, в которых роль потенциальных функций выполняют внутренняя энергия 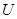 и энтальпия
и энтальпия 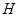 , воспользовавшись неравенством Клаузиуса
, воспользовавшись неравенством Клаузиуса
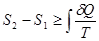 .
.
Пусть в термодинамической системе в ходе любых процессов постоянными поддерживаются энтропия 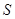 и объем
и объем 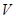 . В этом случае
. В этом случае 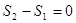 и
и 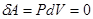 . Тогда неравенство Клаузиуса преобразуется к виду
. Тогда неравенство Клаузиуса преобразуется к виду
 и
и 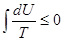 .
.
Поскольку абсолютная температура есть величина существенно положительная (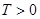 ), то при указанных условиях (
), то при указанных условиях (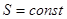 ) и (
) и (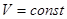 ) самопроизвольные процессы в рассматриваемой системе могут идти лишь с уменьшением её внутренней энергии. Поэтому при достижении минимума внутренней энергии дальнейшие процессы в системе становятся невозможными.
) самопроизвольные процессы в рассматриваемой системе могут идти лишь с уменьшением её внутренней энергии. Поэтому при достижении минимума внутренней энергии дальнейшие процессы в системе становятся невозможными.
Т.о., если объем и энтропия системы поддерживаются постоянными и система в некотором равновесном состоянии достигла минимума внутренней энергии, то равновесие термодинамически устойчиво.
Пусть теперь в ходе любых процессов в системе поддерживаются постоянными энтропия 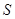 и давление
и давление 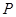 .
.
Перепишем неравенство Клаузиуса в виде
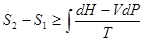 .
.
Поскольку теперь 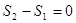 и
и 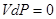 , то
, то
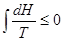 .
.
Используя упомянутое выше свойство температуры, можно заключить, что при условиях, наложенных на систему (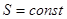 ) и (
) и (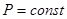 ), самопроизвольные процессы в этой системе могут протекать лишь с уменьшением её энтальпии. Следовательно, при достижении минимума энтальпии, дальнейшие процессы в системе становятся невозможными.
), самопроизвольные процессы в этой системе могут протекать лишь с уменьшением её энтальпии. Следовательно, при достижении минимума энтальпии, дальнейшие процессы в системе становятся невозможными.
Отсюда, если давление и энтропия системы поддерживаются постоянными и система в некотором равновесном состоянии достигла минимума энтальпии, то равновесие термодинамически устойчиво.
Принцип Ле-Шателье – Брауна и устойчивость термодинамического равновесия.
Французским ученым Ле-Шателье (1850-1936) в 1884 г. и, в расширенном виде, немецким физиком Брауном (1850-1918) в 1887 г. был сформулирован принцип, позволяющий предвидеть направление течения процесса в системе, выведенной внешним воздействием из состояния устойчивого равновесия.
Если система находится в состоянии устойчивого равновесия, то всякий процесс, вызванный в ней внешним воздействием или другим первичным процессом, всегда направлен таким образом, что он стремится уничтожить изменения, произведенные внешним воздействием или первичным процессом.
Этот принцип не является столь всеобъемлющим, как второе начало термодинамики. Он не позволяет, в частности, высказывать никаких количественных заключений о поведении системы.
Необходимым условием применимости принципа Ле-Шателье – Брауна является наличие устойчивости равновесия, из которого система выводится внешним воздействием. Он не может быть применен к процессам, переводящим систему в более устойчивое состояние, например, к взрывам.
Принцип Ле-Шателье – Брауна был сформулирован как обобщение знаменитого электродинамического правила Ленца (1804-1865), определяющего направление индукционного тока.
«Тепловая смерть» Вселенной.
Клаузиус, рассматривая всю Вселенную как замкнутую систему, свел содержание второго закона термодинамики к утверждению: «Энтропия Вселенной стремится к максимуму».
Согласно второму началу, любая физическая система, не обменивающаяся энергией с другими системами (для Вселенной в целом, очевидно, такой обмен исключен), стремится к наиболее вероятному равновесному состоянию – к состоянию с максимумом энтропии. При достижении максимума энтропии все виды энергии во Вселенной в конце концов должны перейти в энергию теплового движения, которая равномерно распределится по веществу Вселенной, после чего в ней установится абсолютно равновесное состояние и прекратятся все макроскопические процессы. Такое состояние было названо тепловой смертью Вселенной.
Еще до создания современной космологии были сделаны многочисленные попытки опровергнуть вывод о тепловой смерти Вселенной. Наиболее известной из них является флуктуационная гипотеза австрийского физика Л. Больцмана (1872), согласно которой Вселенная извечно пребывает в равновесном изотермическом состоянии, но по закону случая то в одном, то в другом её месте иногда происходят отклонения от этого состояния. Эти отклонения происходят тем реже, чем большую область они захватывают и чем значительнее степень отклонения.
Современной космологией установлено, что ошибочен как сам вывод о тепловой смерти Вселенной, так, как это ни парадоксально, и ранние попытки его опровержения.
Ошибочность существовавших представлений связана с тем, что при рассмотрении проблемы не принимались во внимание существенные физические факторы, и, прежде всего, тяготение. При учете тяготения оказывается, что однородное изотермическое распределение вещества во Вселенной не является наиболее вероятным и не соответствует максимуму энтропии. Наблюдения показывают, что Вселенная резко нестационарна. Она расширяется, причем, согласно космологической теории, почти однородное в начале расширения вещество в дальнейшем под действием сил тяготения распадается на отдельные объекты, в результате чего образуются скопления галактик, галактики, звезды, планеты. Все эти процессы естественны, идут с ростом энтропии и не требуют нарушения законов термодинамики. Т.о., Вселенная в целом может эволюционировать непрерывно и монотонно, никогда не приходя в состояние термодинамического равновесия. Процессы, идущие во Вселенной, и в будущем с учетом гравитации не приведут к однородному изотермическому состоянию Вселенной – тепловой смерти Вселенной, поскольку Вселенная эволюционирует, оставаясь всегда нестатичной.
Теорема Нернста.
В 1906 г. термодинамика обогатилась новым фундаментальным законом, открытым Нернстом (1864-1941) эмпирическим путем. Этот закон получил название тепловой теоремы Нернста. Теорема Нернста не может быть логически выведена из остальных начал термодинамики, поэтому её часто называют третьим началом термодинамики. Мы не будем останавливаться на первоначальной формулировке теоремы, данной самим Нернстом, поскольку она представляет только исторический интерес, а приведем современную расширенную формулировку теоремы, принадлежащую, в основном, Планку.
Содержание теоремы Нернста сводится к двум утверждениям. Первое утверждение состоит в том, что при приближении к абсолютному нулю энтропия системы стремится к определенному пределу. Поэтому имеет смысл говорить об энтропии тела при абсолютном нуле температуры. Это нетривиальное утверждение.
Если обратиться к термодинамическому определению энтропии
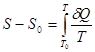 , (!!!.1)
, (!!!.1)
то не очевидно, будет ли интеграл сходиться при  , поскольку в подынтегральном выражении температура
, поскольку в подынтегральном выражении температура 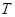 стоит в знаменателе. Поэтому результат будет зависеть от поведения
стоит в знаменателе. Поэтому результат будет зависеть от поведения 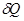 вблизи абсолютного нуля. Т.о., первая часть теоремы Нернста заключается в утверждении, что интеграл (!!!.1) сходится.
вблизи абсолютного нуля. Т.о., первая часть теоремы Нернста заключается в утверждении, что интеграл (!!!.1) сходится.
Вторая часть теоремы Нернста утверждает, что все процессы при абсолютном нуле температур, переводящие систему из одного равновесного состояния в другое равновесное состояние, происходят без изменения энтропии. Из этого утверждения следует, что предел, к которому стремится интеграл (!!!.1) при  , не зависит от того, в каком конечном состоянии окажется система.
, не зависит от того, в каком конечном состоянии окажется система.
Объединяя обе части, можно дать теореме Нернста следующую формулировку. При приближении к абсолютному нулю приращении энтропии 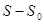 стремится к вполне определенному конечному пределу, не зависящему от значений, которые принимают все параметры, характеризующие состояние системы (объем, давление, агрегатное состояние и пр.).
стремится к вполне определенному конечному пределу, не зависящему от значений, которые принимают все параметры, характеризующие состояние системы (объем, давление, агрегатное состояние и пр.).
Теорема Нернста относится только к термодинамически равновесным состояниям систем. К неравновесным и метастабильным состояниям она неприменима (например, аморфные твердые тела). Строго говоря, к неравновесным, в частности, метастабильным состояниям неприменимо и само понятие температуры.
Если условиться энтропию всякой равновесной системы считать равной нулю (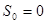 ) при абсолютном нуле температуры (
) при абсолютном нуле температуры (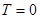 ), то энтропия, определяемая выражением (!!!.1), будет называться абсолютной энтропией. Тогда теорема Нернста может быть сформулирована следующим образом.
), то энтропия, определяемая выражением (!!!.1), будет называться абсолютной энтропией. Тогда теорема Нернста может быть сформулирована следующим образом.
При приближении к абсолютному нулю абсолютная энтропия системы стремится также к абсолютному нулю независимо от того, какие значения принимают все параметры, характеризующие состояние системы.
Однако такой выбор аддитивной постоянной в выражении для энтропии есть не более как произвольное соглашение. Энтропия же по своей сущности всегда определена с точностью до произвольной аддитивной постоянной. Фактическое содержание теоремы Нернста никак не связано с выбором этой постоянной, а целиком сводится к двум сформулированным выше утверждениям.
Теореме Нернста может быть дана и другая эквивалентная формулировка.
При помощи конечной последовательности термодинамических процессов нельзя достичь температуры, равной абсолютному нулю.
Приближение к нулю (или другому договорному минимуму) энтропии 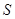 тел при устремлении их температуры
тел при устремлении их температуры 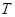 к абсолютному нулю означает, что тела при таких температурах обладают минимально возможной степенью беспорядка. Можно предположить, что при таких условиях могут наблюдаться явления, которые не могли быть реализованы в состояниях, характеризуемых существенно более высокой степенью беспорядка. Действительно, при очень низких температурах начинают в макроскопических масштабах проявляться некоторые квантовые эффекты – сверхпроводимость металлов (полная потеря сопротивления электрическому току, Камерлинг-Оннес, 1911 г.), сверхтекучесть жидкого гелия (потеря вязкости при температурах
к абсолютному нулю означает, что тела при таких температурах обладают минимально возможной степенью беспорядка. Можно предположить, что при таких условиях могут наблюдаться явления, которые не могли быть реализованы в состояниях, характеризуемых существенно более высокой степенью беспорядка. Действительно, при очень низких температурах начинают в макроскопических масштабах проявляться некоторые квантовые эффекты – сверхпроводимость металлов (полная потеря сопротивления электрическому току, Камерлинг-Оннес, 1911 г.), сверхтекучесть жидкого гелия (потеря вязкости при температурах 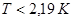 , позволяющаяся обтекать препятствия, не испытывая рассеяния и проникать через щели
, позволяющаяся обтекать препятствия, не испытывая рассеяния и проникать через щели 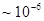 см, П.Л. Капица).
см, П.Л. Капица).
Date: 2015-05-04; view: 2078; Нарушение авторских прав