Тепловые машины

Принципиальная схема тепловой машины.

Термодинамика возникла как наука, исследующая принципиальные возможности получения полезной механической работы за счет внутренней энергии тела. Устройства, предназначенные для получения работы за счет тепловой энергии, называются тепловыми машинами.

В XIX веке была надежда изобрести машину, которая бы отбирала тепловую энергию от окружающей среды и всю ее превращала в работу. Вечный двигатель второго рода - передача тепла от холодного тела к горячему без затрат внешней работы.

Сади Карно (1796-1832), Рудольф Клаузиус (1822-1888), Вильям Томсон (лорд Кельвин, 1824-1907) установили второе начало термодинамики: невозможность самопроизвольного превращения тепла в работу, или, иначе, невозможность вечного двигателя второго рода.

Первое начало (закон сохранения энергии) не ограничивает эти процессы: перевод тепла в работу и обратно. Запрет на превращение тепла в работу, налагаемый вторым началом, относится к замкнутой системе, состоящей из находящихся в непрерывном контакте тел с различной температурой.

Однако, если между горячим и холодным телом поместить разъединяющее их третье тело, то за счет компенсирующих процессов можно осуществить и превращение тепла в работу и перенос тепла от холодного к горячему. На это обратил внимание С. Карно, который разработал принципиальную схему тепловой машины.

Принципиальная схема тепловой машины изображена на рисунке.

Различные формулировки основного постулата, выражающего второе начало термодинамики.

Чтобы прийти к формулировке постулата второго начала термодинамики, рассмотрим схематически работу тепловой машины.

В цилиндре машины помещается газ, называемый рабочим телом. Приведем дно

цилиндра в тепловой контакт с нагревателем, т.е. телом, температура которого выше

температуры газа в цилиндре. Рабочее вещество получит от нагревателя теплоту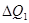

и, расширяясь, совершит положительную работу (кривая ). Согласно первому

началу

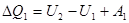. (1.40)

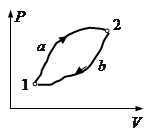Вернем поршень в исходное положение, сжав газ, сделав это так, чтобы

работа 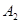, затраченная на сжатие, была меньше . Для этого приведем

дно цилиндра в тепловой контакт с холодильником, т.е. телом, температура

которого ниже температуры газа в цилиндре (кривая ). По первому

началу количество теплоты , отданное холодильнику

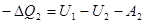. (1.41)

Т.о., тепловая машина совершила круговой процесс, в результате которого нагреватель отдал количество теплоты 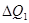, холодильник получил количество теплоты , а количество теплоты пошло на производство работы 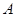. Из (1.40) и (1.41) получаем

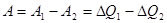. (1.42)

Чтобы в работе тепловой машины природа вспомогательного рабочего тела не была существенна, она должна выполнять круговой процесс, в результате которого тело переходит в начальное состояние. При этом внутренняя энергия не изменяется. Это и есть цикл.

Введем коэффициент 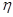, характеризующий полезное потребление тепла, называемый коэффициентом полезного действия (КПД) тепловой машины:

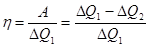. (1.43)

Понятно, что хотелось бы использовать тепло на все 100%, т.е. построить периодически действующую тепловую машину без холодильника ( ).

Возможность построения такой машины не противоречит закону сохранения энергии. А по своему практическому значению она почти так же привлекательна, как перпетуум мобиле, потому что могла бы производить работу, не восстанавливая состояния источника, за счет которого эта работа производится.

В. Оствальд (1853-1932) назвал такую машину перпетуум мобиле второго рода в отличие от вечного двигателя, производящего работу из ничего, возможность которого отрицается первым началом термодинамики.

С. Карно понял, что такая тепловая машина принципиально невозможна.

Для наглядности работу тепловых двигателей он сравнивал с работой двигателей водяных. Производство работы в последних связано с падением воды на более низкий уровень, однако вода не может самопроизвольно подниматься снизу вверх, т.е. раньше или позже придется затратить работу на восстановление начального состояния системы.

Аналогично возможность производства работы тепловыми двигателями по Карно обусловлена самопроизвольным переходом теплоты от более нагретого тела к менее нагретому. Однако любой нагреватель обладает конечным запасом теплоты, поэтому этот запас необходимо периодически пополнять, возвращая тепловой резервуар нагревателя в исходное состояние, что требует определенных затрат.

Опытные факты говорят против возможности построения перпетуум мобиле второго рода. Поэтому невозможность построения такого двигателя была возведена в постулат. Он называется постулатом второго начала термодинамики и является обобщением опытных фактов. Доказательством этого постулата служит согласие всех вытекающих из него следствий с опытом. До сих пор, применяя этот постулат к макроскопическим системам, физика нигде не натолкнулась на противоречия.

Формулировка Томсона-Планка.

Формулировка В. Томсона: Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара.

Если конкретизировать вид внешней работы, можно видоизменить формулировку постулата.

Формулировка М. Планка: Невозможно построить периодически действующую тепловую машину, единственным результатом работы которой было бы поднятие груза за счет охлаждения теплового резервуара.

Тепловым резервуаром называют тело или систему тел, находящуюся в состоянии теплового равновесия и обладающую запасом внутренней энергии. Тепловой резервуар не совершает макроскопической работы, а может передавать свою внутреннюю энергию другому телу или системе тел. Тело (система тел), производящее работу за счет внутренней энергии теплового резервуара, называется рабочим телом. Охлаждение теплового резервуара следует понимать как уменьшение запаса его внутренней энергии.

Принципиально важным в формулировке Планка является указание на периодичность действия машины, точно так же как в формулировке Томсона существенно, что процесс должен быть круговым. Действительно, например, в процессе изотермического расширения идеального газа теплота, заимствованная у теплового резервуара, может полностью переходить в макроскопическую работу ( , т.к. ), что не противоречит постулату второго начала. Однако, невозможно, не производя никаких изменений во всех остальных телах, полностью преобразовать всю полученную из резервуара теплоту 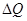исключительно в макроскопическую работу 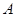, совершая круговой процесс.

Формулировка Планка отличается от формулировки Томсона лишь по форме. Поэтому для удобства называют процессом Томсона-Планка воображаемый круговой процесс, единственным результатом которого является производство работы за счет охлаждения теплового резервуара. Тогда постулат второго начала термодинамики сводится к утверждению, что процесс Томсона-Планка невозможен.

Формулировка Клаузиуса.

Теплота не может самопроизвольно переходить от тела, менее нагретого, к телу более нагретому.

Под теплотой здесь надо понимать внутреннюю энергию тела.

Постулат, сформулированный Клаузиусом, не исключает принципиальной возможности передачи тепла от холодного тела к горячему. Он утверждает, что невозможно каким бы то ни было способом целиком передать забранную у менее нагретого тела теплоту и передать её более нагретому, не произведя в природе или во всех остальных телах никаких изменений. Именно в этом и состоит смысл слова «самопроизвольно», употребленного в формулировке Клаузиуса. Любой воображаемый процесс, в котором осуществляется такая передача тепла, называется процессом Клаузиуса. Т.о., постулат утверждает, что процесс Клаузиуса невозможен.

Если допустить сопутствующие процессы в окружающих телах, то передача теплоты от менее нагретого тела к более нагретому становится возможной. Такие процессы называются компенсирующими процессами, или компенсациями. Для примера можно обратиться к обычному бытовому холодильнику. Принцип его работы не противоречит постулату Клаузиуса, поскольку переход теплоты от менее к более нагретому телу происходит не самопроизвольно, сопровождается работой электродвигателя.

Невозможен самопроизвольный (происходящий без изменения в окружающих телах) переход тепла от менее нагретого к более нагретому телу.

Простейшая холодильная машина приведена на рисунке.

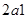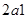По сути, это та же тепловая машина, которая упоминалась в начале параграфа, с тем лишь отличием, что расширение рабочего вещества следует проводить по пути , а сжатие – по кривой , лежащей выше. Совершая расширение , машина будет заимствовать от холодильника теплоту ; при сжатии по кривой она передает нагревателю теплоту 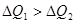. При этом над машиной будет произведена положительная внешняя макроскопическая работа 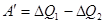. Производство этой работы и является компенсирующим процессом.

Эквивалентность формулировок второго начала термодинамики Томсона-Планка и Клаузиуса.

Из невозможности процесса Томсона-Планка следует невозможность процесса Клаузиуса.

Проведем доказательство методом от противного. Пусть процесс Томсона-Планка невозможен, а процесс Клаузиуса возможен. Проведем круговой процесс, в результате которого тепловая машина получит от нагревателя теплоту 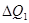, передаст холодильнику теплоту и совершит положительную работу 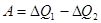. Затем с помощью процесса Клаузиуса теплоту отнимем у холодильника и вернем нагревателю. Тогда получится круговой процесс, единственным результатом которого является производство работы 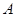за счет эквивалентного ей количества теплоты 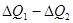, полученного от нагревателя. Никаких других изменений в окружающей среде не произойдет. Т.о., будет проведен процесс Томсона-Планка, который по предположению невозможен. Полученное противоречие и доказывает наше утверждение.

Соответственно, из невозможности процесса Клаузиуса вытекает невозможность процесс Томсона-Планка.

Предположим, что процесс Томсона-Планка возможен. Тогда, используя этот круговой процесс, отнимем от менее нагретого тела теплоту 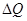и за счет этой теплоты произведем механическую работу, подняв груз. Затем энергию поднятого груза используем для нагревания (например, путем трения) более нагретого тела. В результате теплота 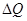от менее нагретого перейдет к более нагретому телу, причем никаких других изменений в окружающих телах не произойдет. Но это есть процесс Клаузиуса, который по предположению невозможен. Это противоречие и доказывает высказанное утверждение. При доказательстве был использован не только постулат Клаузиуса, но и утверждение, что потенциальная энергия поднятого груза может быть целиком превращена в теплоту. Это утверждение является следствием опыта. Согласно первому началу количество полученной теплоты точно равно потерянной потенциальной энергии груза.

Т.о., постулаты Томсона-Планка и Клаузиуса эквивалентны.

Обратимые и необратимые процессы.

Если в результате какого-либо процесса система переходит из состояния 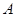в состояние 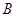и может быть возвращена хотя бы одним способом в исходное состояние 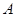так, чтобы в окружающих телах не произошло никаких изменений, процесс называется обратимым. Если такой возврат невозможен, то процесс называется необратимым.

Примерами обратимых процессов являются изобарический, изохорный, изотермический, адиабатический;

необратимых – переход тепла от горячего тела к холодному, получение тепла через трение.

Если систему можно вернуть в начальное состояние произвольным способом, не требуя, чтобы она проходила через ту же последовательность состояний что и в прямом процессе, то прямой процесс называют обратимым в широком смысле.

Если возможен обратный процесс, переводящий систему в исходное состояние через ту же последовательность состояний, которую она прошла в прямом процессе, то процесс 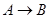называют обратимым в узком смысле.

Всякий процесс, обратимый в узком смысле, очевидно, обратим и в широком смысле.

Любой квазистатический процесс обратим в узком смысле слова. Для того, чтобы убедиться в этом,

достаточно изменить знаки приращений всех параметров на обратные. Поэтому квазистатический процесс может идти как в прямом, так и в обратном направлении.

Цикл Карно.

В термодинамике из множества круговых процессов особое значение с точки зрения определения возможности превращения тепла в механическую работу имеет круговой процесс, называемый циклом Карно. Это квазистатический круговой процесс, образованный из 2-х адиабат и 2-х изотерм. Рассмотрим в качестве рабочего тела идеальный газ, помещенный в цилиндрический сосуд с поршнем.

Сначала система, имеющая температуру , приводится в тепловой контакт с нагревателем, имеющим ту же температуру . Затем, бесконечно медленно уменьшая внешнее давление, систему заставляют квазистатически расширяться по изотерме 1-2. При этом система

производит работу 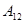против внешнего давления, заимствуя

теплоту 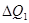от нагревателя. После этого систему адиабатически

изолируют и заставляют квазистатически расширяться по адиабате

2-3 до достижения ею температуры холодильника 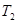. При этом

система снова совершает работу 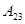против внешнего давления.

В состоянии 3 систему приводят в тепловой контакт с холодильником

и, непрерывно увеличивая давление, изотермически сжимают до

состояния 4. В процессе 3-4 работа производится над системой (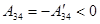 ), и система отдает холодильнику теплоту . Состояние 4 выбирается таким, чтобы можно было квазистатическим сжатием вернуть систему по адиабате 4-1 в исходное состояние 1, совершая работу над системой ( ).

В результате кругового процесса Карно внутренняя энергия системы не изменится, поэтому произведенная системой работа равна

. (!.1)

Коэффициент полезного действия тепловой машины определяется выражением (1.43)

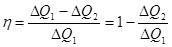. (!.2)

Система участвует в теплообмене, получая теплоту от нагревателя в процессе 1-2 ( ):

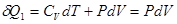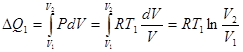; , (!.3)

и, отдавая теплоту холодильнику в процессе 3-4 ( ):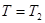

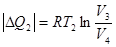. (!.4)

Адиабаты 2-3 и 3-4 описываются уравнениями Пуассона

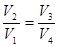, поделив, получаем . (!.5)

Подставляя (!.3), (!.4) и (!.5) в (!.2), получаем

. (!.6)

Т.о., коэффициент полезного действия для цикла Карно:

. (!.6)

Мы получили аналитическое выражение знаменитой теоремы Карно.

Заметим, что выбор адиабатического и изотермического процессов для построения цикла Карно не случаен, а определяется экономической целесообразностью, поскольку эти процессы обладают наибольшими коэффициентами полезного действия среди всех квазистатических процессов.

Теорема Карно.

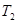Коэффициент полезного действия тепловой машины, работающей по циклу Карно, зависит только от температур и нагревателя и холодильника, но не зависит от устройства машины, а также вида используемого рабочего вещества.

Насколько случайно в полученное выражение (!.6) не вошли характеристики рабочего тела, в данном случае – газа? Основываясь на втором начале термодинамики, можно показать, что КПД цикла Карно не зависит от выбора рабочего тела.

Рассмотрим две машины Карно имеющие общие нагреватель и холодильник с температурами и 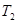, соответственно, но использующие разные рабочие вещества. Пусть теперь КПД первой машины равен 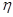, а второй - 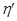, причем . Покажем, что это допущение приводит к противоречию с постулатом второго начала.

Цикл Карно квазистатический, поэтому он может совершаться как в прямом, так и в обратном направлении. Пусть первая машина проходит 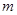циклов в прямом направлении. При этом она отберет от нагревателя теплоту 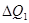, передаст холодильнику теплоту и произведет работу 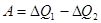, например, подняв груз.

Остановим после этого первую машину и используем потенциальную энергию поднятого груза, чтобы привести в действие вторую машину в обратном направлении.

Очевидно, что вторая машина Карно будет работать как холодильная машина. Пусть в результате 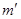циклов она заберет от холодильника теплоту , передаст теплоту нагревателю и совершит работу .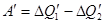

Итог работы машин в циклах выражается уравнением:

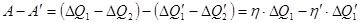. (!.7)

Положим в основу доказательства постулат Клаузиуса.

Выберем целые числа 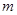и 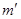так, чтобы суммарная работа, выполненная обеими машинами, равнялась нулю:

. (!.8)

Тогда результат завершившихся круговых процессов следующий:

нагреватель получил теплоту

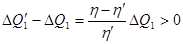, (!.9)

холодильник отдал теплоту

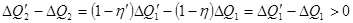. (!.10)

Никаких других изменений не произошло. Поэтому единственным результатом процесса получился переход теплоты от менее нагретого к более нагретому телу, что противоречит постулату Клаузиуса и доказывает теорему Карно.

Можно провести доказательство, положив в основу постулат Томсона-Планка (Сивухин, т.2, с. 102-103).

Неравенство Клаузиуса.

Используем рассуждения, проведенные при доказательстве теоремы Карно, для получения весьма важного следствия.

Рассмотрим произвольную термодинамическую систему 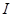, которая может обмениваться теплом с двумя тепловыми резервуарам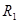и и , температуры и 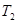которых поддерживаются постоянными.

Отвлечемся от понятий «нагреватель» и «холодильник» и поступим следующим образом. Будем считать количество теплоты, полученное системой 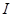(отданное резервуаром), положительным, а отданное системой 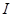(полученное резервуаром) – отрицательным. При таком подходе окончательный результат формулируется симметрично относительно обоих резервуаров.

Пусть система 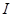совершила произвольный круговой процесс (обратимый или необратимый), в котором она получила количество теплоты 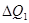от резервуара 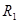и от резервуара . Поскольку система вернулась в исходное состояние, полное количество теплоты 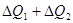, полученное ею, будет равно работе, которую произвела система.

После завершения системой 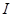кругового процесса подключим к этим же резервуарам машину Карно, теплоизолировав с этого момента систему 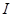. Теперь резервуары 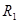и могут обмениваться теплом только с машиной Карно.

Пусть машина Карно совершила круговой процесс, в ходе которого она заимствовала теплоту от резервуара 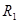и теплоту от резервуара . Машина Карно обратима, поэтому может работать как двигатель и как холодильник. Кроме того, изотерма цикла Карно, а, следовательно, и работа могут быть сделаны сколь угодно малыми. С другой стороны, машина Карно может совершать много одинаковых циклов. Поэтому машина Карно позволяет получать как положительную, так и отрицательную работу любой наперед заданной величины. Т.о., образом всегда можно достичь, чтобы одна из величин или приняла произвольное, положительное или отрицательное, значение.

По определению

, (!.11)

или

. (!.12)

Объединим систему 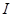и машину Карно в одну сложную систему. Циклы, последовательно совершенные системой 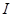и машиной Карно, объединим в один общий круговой процесс.

В этом процессе сложная система

1. получила от резервуара 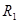теплоту ;

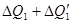2. получила от резервуара теплоту ;

3. совершила работу .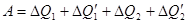

Дальнейшие рассуждения будем основывать на постулате Томсона-Планка.

Подберем, используя возможности машины Карно, так, чтобы получилось

. (!.13)

Тогда из (!.12) получим

. (!.14)

Понятно, что при условии (!.13) в результате кругового процесса состояние резервуара 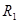не изменится, а тепловой резервуар отдаст количество теплоты, равное

. (!.15)

За счет этого тепла производится эквивалентная работа

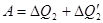. (!.16)

Если предположить, что произведенная работа положительна, то получим процесс Томсона-Планка, поскольку единственным результатом является получение работы за счет теплоты, взятой от одного источника, что невозможно. Поэтому должно быть 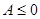. Поскольку температура, измеренная по абсолютной шкале, является существенно положительной величиной, то приходим к выражению

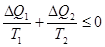. (3.17)

Т.о., мы получили частный случай неравенства Клаузиуса.

Неравенство Клаузиуса, конечно, можно получить, исходя из постулата Клаузиуса.

Для этого выберем таким, чтобы

, или . (!.18)

Тогда единственным результатом кругового процесса, совершенного сложной системой, будет передача теплоты 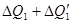от резервуара 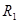к резервуару . Найдем эту теплоту.

Теплоту можно определить из (!.18), воспользовавшись (!.12),

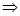
. (!.19)

Тогда

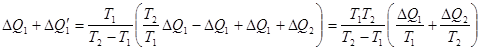. (!.20)

Согласно постулату Клаузиуса , если , и 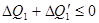, если .

В обоих случаях снова получаем

.

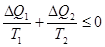Теперь, используя полученное соотношение (3.17), докажем вторую теорему Карно.

Вторая теорема Карно.

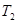Вернемся в этом параграфе к первоначальному разделению тепловых машин на нагреватель с температурой и холодильник ( ). Количество теплоты будем, как и прежде, считать положительным, если холодильник его получает. При таком выборе знаков (3.17) принимает вид

.

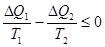Отсюда легко получить

, или . (!.21)

Коэффициент полезного действия всякой тепловой машины не может превосходить коэффициент полезного действия идеальной машины, работающей по циклу Карно с теми же температурами холодильника и нагревателя.

Т.о., мы доказали вторую теорему, принадлежащую Карно, которая позволяет оценить верхний предел КПД тепловой машины.

Неравенство Клаузиуса (общий вид).

Чтобы получить фундаментальное соотношение, называемое неравенством Клаузиуса в общем виде, рассматривают совершаемый термодинамической системой 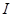круговой процесс (обратимый или необратимый), в ходе которого она заимствует у произвольного числа тепловых резервуаров 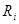количества теплоты

,

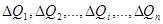за счет чего производит эквивалентную работу

.

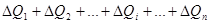Далее систему 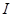теплоизолируют и для обеспечения необходимого теплового баланса привлекают 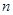машин Карно, совершающих круговой процесс, и вспомогательный тепловой резервуар , настолько большой, чтобы в процессе теплообмена его температура не менялась.

Схема такой установки показана на рисунке.

Основываясь на приведенной схеме, и, например, постулате Томсона-Планка, приходят к неравенству, имеющему вид (3.22).

. (3.22)

Кружок у знака суммы означает, что соотношение

(3.22) относится к круговому процессу, выполненному

системой .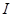

Для того, чтобы придать фундаментальность

неравенству (3.22), т.е. обосновать его применимость к

произвольной термодинамической системе,

совершающей круговой процесс, проведем поэтапно

следующие рассуждения.

1. Вспомогательные приспособления – машины

Карно и тепловой резервуар - использовались только для построения схемы доказательства и были привлечены уже после того, как круговой процесс в термодинамической системе 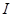уже произошел. Поэтому их наличие не может отразиться на справедливости полученного соотношения (3.22).

2. Предполагалось, что резервуары 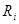не

обмениваются теплотой между собой. В действительности такой теплообмен не играет роли, т.е. неравенство (3.22) остается справедливым и при его наличии, а при необходимости всегда можно ввести адиабатические перегородки, исключающие указанный теплообмен.

3. Предполагалось, что тепловые резервуары достаточно (в пределе, бесконечно) велики, чтобы отбор у них тепла не влиял на температуру резервуаров, которая должна оставаться постоянной.

В общем случае резервуары должны быть конечными, а их температуры могут произвольно меняться во времени. Формально этот случай сводится к рассмотренному следующим образом. Разобьем процесс теплообмена, в результате которого резервуар 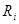отдает системе 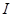теплоту 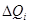на сколь угодно большое число 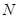бесконечно малых процессов, в которых от резервуара систему передается бесконечно малое количество теплоты при постоянной для каждого из этих процессов температуре. Смысл такой операции в следующем. Один большой резервуар с переменной температурой эквивалентен 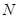последовательно включаемым резервуарам с разными, но постоянными температурами, отдающими в свою очередь системе 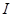теплоту и остающимися все остальное время теплоизолированными.

4. Такой подход позволяет при окончательной формулировке неравенства Клаузиуса пользоваться представлением о теплообмене системы 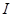с окружающей средой, не вводя в рассмотрение тепловые резервуары 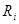. При этом температура 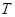окружающей среды может меняться как во времени, так и в пространстве.

Итак, фундаментальное соотношение, называемое неравенством Клаузиуса, имеет вид:

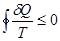. (3.22)

Date: 2015-05-04; view: 694; Нарушение авторских прав