Непосредственные умозаключения. Непосредственными называются умозаключения из одной посылки, являющейся категорическим суждением (общеутвердительным

Непосредственными называются умозаключения из одной посылки, являющейся категорическим суждением (общеутвердительным, общеотрицательным, частноутвердительным или частноотрицательным атрибутивным суждением). Непосредственными умозаключениями являются превращение и обращение категорических суждений.

Превращение категорического суждения — это изменение его качества одновременно с заменой предиката на противоречащий ему термин. Превращение осуществляется в соответствии со следующими схемами:

Все S суть Р Некоторые S суть Р

А: —————————— I: ——————————

Ни одно S не суть не- Р Некоторые S не суть не- Р

Ни одно S не суть Р Некоторые S не суть Р

Е: —————————— О: ——————————

Все S суть не- Р Некоторые S суть не- Р

Пример:

Некоторые материалисты — метафизики. ____

Некоторые материалисты не суть не метафизики.

Обращение категорического суждения заключается в перемене местами его субъекта и предиката в соответствии со следующими схемами:

Все S суть Р

А: __________________

Некоторые Р суть S

Общеутвердительное суждение обращается с ограничением, т.е. вывод по схеме:

Ни один S не суть Р

Все Р суть S не является правильным

Некоторые S суть Р Ни один S не суть Р

I: —————————— Е: ——————————

Некоторые Р суть S Ни один Р не суть S

О: Частноотрицательное суждение не обращается, т.е. вывод по схеме:

Некоторые S не суть Р

Некоторые Р не суть S не является правильным.

Замечание. Суждения с субъектами, являющимися мнимыми именами, принимаются за бессмысленные. Не обращаются суждения, предикатами которых являются мнимые имена. Если это ограничение игнорировать, то из истинного суждения можно получить ложное. Кроме того, не рассматриваются суждения, в которых объединения объемов субъекта и предиката образуют универсум рассуждения.

Пример:

Ни один философ не открыл секрет физического бессмертия (человека). ___________________________________________________________

Ни один человек, открывший секрет физического бессмертия, не является философом.__________________________________________________________

Каждый человек, открывший секрет физического бессмертия, суть не философ. (Результат превращения предшествующего суждения).

Некоторые не философы открыли секрет физического бессмертия (человека).

К непосредственным умозаключениям относятся выводы, заключающиеся в превращении категорического суждения и обращении результата превращения (противопоставление предикату), а также в обращении категорического суждения и превращении результата обращения (противопоставление субъекту). Противопоставление предикату — это умозаключение, в котором субъектом заключения является термин, противоречащий предикату посылки, предикатом — субъект посылки, и заключение и посылка различны по качеству. Противопоставление субъекту — это умозаключение, в котором субъектом заключения является предикат посылки, предикатом заключения — термин, противоречащий субъекту посылки и заключение и посылка различны по качеству. Противопоставление предикату и противопоставление субъекту можно осуществлять и анализировать поэтапно (например, в случае противопоставления предикату сначала произвести превращение, а затем осуществить правильное обращение).

Общие схемы противопоставления предикату:

____ ... S суть Р___

... не- Р не суть S

... S не суть Р____

…не- Р суть S

Общие схемы противопоставления субъекту:

____ ... S суть Р___

… Р не суть не- S

... S не суть Р____

… Р суть не- S

Замечание. Нельзя делать выводы, называемые противопоставлением предикату и противопоставлением субъекту, из суждений с предикатами, являющимися, соответственно, универсальными и мнимыми именами.

Пусть дано умозаключение:

Некоторые хозрасчетные предприятия являются рентабельными.____

Некоторые нерентабельные предприятия не являются хозрасчетными.

Это умозаключение подпадает под общую схему противопоставления предикату. Чтобы проверить, правильное оно или нет, нужно произвести превращение исходного суждения:

Некоторые хозрасчетные предприятия являются рентабельными

Некоторые хозрасчетные предприятия не являются нерентабельными.

Затем правильно произвести обращение результата превращения:

Некоторые хозрасчетные предприятия не являются нерентабельными.

?

Частноотрицательное суждение не обращается. Следовательно, приведенное выше умозаключение не является правильным.

Для письменной проверки правильности непосредственных умозаключений можно использовать круговые схемы Эйлера.

Пусть дано умозаключение (противопоставление субъекту):

Некоторые материалисты (S) — метафизики (Р)

Некоторые метафизики (Р) не суть не материалисты (не- S)

В посылке этого умозаключения утверждается, что некоторые элементы объема имени S входят в объем имени Р. Поскольку слово “некоторые” употребляется в смысле “по крайней мере некоторые, а, может быть, и все”, то в общем случае следует допустить четыре возможности:

Заштрихованная поверхность соответствует тем элементам объема имени S, которые входят в объем имени Р. Прямоугольником представлен универсум рассуждения — в данном случае, например, класс философов.

Что говорится в заключении? Некоторые Р не суть не -S. Во всех ли случаях на приведенных схемах отражено, что (по крайней мере) некоторые элементы объема термина Р не включаются в объем термина не- S? Заштрихуем на схемах горизонтальными линиями поверхности, соответствующие объему термина не- S. Для этого схемы начертим еще раз:

Очевидно, что во всех четырех случаях некоторые Р не являются элементами не- S. Эти элементы объема термина Р представлены поверхностями, заштрихованными наклонными линиями. Анализируемое рассуждение является правильным.

Чтобы установить, что непосредственное умозаключение не является правильным, нет необходимости рассматривать все возможные отношения между субъектом и предикатом посылки, при которых она является истинной. Достаточно найти один опровергающий случай.

Рассмотрим схему умозаключения, напоминающего обращение общеутвердительного суждения:

__ Все S суть Р__

Все Р суть S

Одной из схем, представляющих возможные отношения между S и Р, при которых посылка истинна, является следующая:

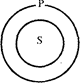
Очевидно, что в этом случае нельзя сделать вывод о том, что все Р суть S, т.е. обращение общеутвердительного суждения без ограничения невозможно (является неправильным).

Покажем, что обращение частноотрицательного суждения

Некоторые S не суть Р

Некоторые Р не суть S

не являются правильным умозаключением. Одной из схем, представляющих возможные отношения между S и Р при истинности частноотрицательного суждения, является:

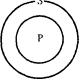
Нельзя утверждать, что некоторые Р не суть S.

Метод, который применен для исследования непосредственных умозаключений, заключается в выполнении следующих действий: первое — выявить все возможные отношения между терминами посылки, при которых она является истинной; второе — проверить, истинно ли заключение при каждом из выявленных отношений. Если да, то умозаключение правильное. Если заключение ложно хотя бы при одном из этих отношений — умозаключение неправильное.

Date: 2015-06-06; view: 504; Нарушение авторских прав