Простые суждения

Простым называется суждение, в котором нельзя выделить правильную часть, т.е. часть, не совпадающую с целым, в свою очередь являющуюся суждением. Среди простых суждений выделяют атрибутивные суждения и суждения об отношениях.

Атрибутивные суждения. Атрибутивными называются суждения, в которых выражается принадлежность предметам свойств или отсутствие у предметов каких-либо свойств. Атрибутивные суждения можно истолковать как суждения о полном или частичном включении или невключении одного множества предметов в другое или как суждения о принадлежности или непринадлежности предмета классу предметов.

Примеры: “Некоторые обвиняемые являются несовершеннолетними”, “Ни один кит не является рыбой”, “Аргентина — республика”. В первом суждении говорится, что множество обвиняемых частично (или полностью) включается в множество несовершеннолетних, а во втором говорится, что множество китов и множество рыб не имеют общих элементов, в третьем — что Аргентина — элемент класса республик.

В каждом атрибутивном суждении есть субъект (логическое подлежащее), предикат (логическое сказуемое) и связка (связка иногда лишь подразумевается), а в некоторых имеются еще так называемые кванторные (количественные) слова (“некоторые”, “все”, “ни один” и др.). Субъект и предикат называются терминами суждения.

Субъект часто обозначается латинской буквой S (от слова “subjectum”), а предикат — Р( от слова “praedicatum”). В суждении “Некоторые науки не являются гуманитарными” субъект (S) — “науки”, предикат (P) — “гуманитарные”, связка — “не являются”, а “некоторые” — кванторное слово.

Атрибутивные суждения делятся на виды “по качеству” и “по количеству”.

По качеству они делятся на утвердительные и отрицательные. В утвердительных выражается полное или частичное включение класса предметов в класс предметов или же принадлежность некоторого предмета классу предметов. В отрицательных — невключение класса предметов, части класса, в некоторый класс или непринадлежность предмета классу предметов. Суждение “Полынь является лекарственным растением” — утвердительное, а суждение “Демокрит не является идеалистом” — отрицательное.

По количеству атрибутивные суждения делятся на единичные, общие и частные. В единичных суждениях выражается принадлежность или непринадлежность предмета классу предметов. Пример:

“Австрия — европейская страна”. В общих — полное включение или невключение класса предметов в класс. Примеры: “Все сделки, не соответствующие требованиям закона, являются недействительными”, “ Ни одна звезда не является обитаемой”.

В частных суждениях выражается частичное включение или невключение класса предметов в класс предметов. Примеры: “Некоторые преступления не являются преднамеренными”, “Некоторые философы являются ораторами”.

В частных суждениях слово “некоторые” употребляется в смысле “по крайней мер один, а может быть, и все”, поэтому, например, суждение “Некоторые белки не являются живыми существами” истинно, так как ни один белок не является живым существом.

В определенном смысле единичные суждения можно отождествить с общими.

При решении вопроса о правильности и неправильности рассуждении и в некоторых других случаях используется так называемое объединенное деление атрибутивных суждений по качеству и количеству на общеутвердительные, общеотрицательные, частноутвердительные и частноотрицательные.

Общеутвердительными являются суждения, которые одновременно общие и утвердительные.

Структура общеутвердительного суждения такова: “Все S суть Р ”. Общеутвердительное суждение обозначается латинской буквой А.

Общеотрицательное суждение является одновременно общим и отрицательным. Оно имеет структуру: “Ни одно S не суть Р ” и обозначается латинской буквой Е.

Частноутвердительное суждение — одновременно частное и утвердительное. Его структура: “Некоторые S суть Р ”. Обозначается оно латинской буквой I.

Частноотрицателыюе суждение — это суждение, являющееся одновременно частным и отрицательным. Оно обозначается латинской буквой О и имеет структуру: “Некоторые S не суть Р”.

Субъект и предикат суждения могут быть распределены (взяты в полном объеме) или не распределены (взяты не в полном объеме). В общих суждениях распределены субъекты, а в отрицательных — предикаты. Если объемы субъектов и предикатов представить в виде кругов, то распределенность терминов можно пояснить следующим образом.

В высказываниях вида “Все S суть Р ” утверждается, что класс S полностью включается в классР, т.е. оно истинно при следующих объемных отношениях между S и Р:

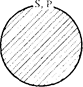
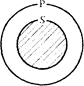
Заштрихованная поверхность соответствует классу предметов, к которым непосредственно относится утверждение.

В высказываниях вида “Некоторые S суть Р ” утверждается, что (по крайней мере) часть класса S включается в класс Р, т.е. оно истинно в следующих случаях:

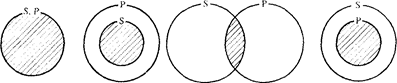
Заштрихованной поверхности соответствует часть класса S, которая включается в Р.

В высказываниях вида “Ни один S не суть Р ” утверждается, что классы S и Р не имеют общих элементов объемов, т.е. оно истинно в случае:

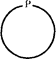
Заштрихованная поверхность соответствует классу предметов, к которым непосредственно относится утверждение.

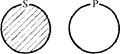
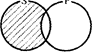
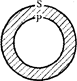
В высказываниях вида “Некоторые S не суть Р ” утверждается, что часть класса S не включается в класс Р, т.е. оно истинно в случаях:

Заштрихованной поверхности соответствует часть класса S, которая не включается в Р.

Термин распределен в суждении, если он взят в нем в полном объеме, т.е. либо полностью включается, либо полностью исключается из класса, которому соответствует заштрихованная поверхность на любой диаграмме, отображающей истинное суждение данного типа.

Если распределенный термин пометить знаком “+”, а нераспределенный — знаком “—”, то получаем: все S⁺ суть Р^—; ни одно S⁺ не суть P ⁺, некоторый S^— суть Р^—; некоторые S^— не суть P ⁺.

Date: 2015-06-06; view: 497; Нарушение авторских прав