Закон Био-Савара-Лапласа. Магнитное поле проводников с током

Рис. 3.7. Магнитное поле, создаваемое элементом тока

Био и Савар в 1820 г. провели исследования магнитных полей, создаваемых проводниками разной формы. Они установили, что магнитная индукция во всех случаях пропорциональна величине тока и сложным образом зависит от расположения проводников. Лаплас, обработав их данные, получил формулу, называемую законом Био-Савара-Лапласа:

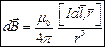(3.7)

Здесь 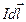- элемент тока (произведение силы тока на элемент длины проводника), совпадающий по направлению с током; 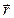- радиус-вектор, проведенный в ту точку поля, где определяется магнитная индукция (рис. 3.7); m₀ - магнитная постоянная (см. раздел 3.1). Направление элементарной магнитной индукции 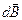совпадает с направлением вектора, равного векторному произведению 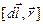. Модуль определим, используя выражение для модуля векторного произведения:

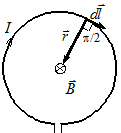Рис. 3.8. К определению магнитной индукции в центре витка

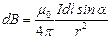. (3.8)

Применим Закон Био-Савара-Лапласа для определения магнитной индукции в центре кольцевого проводника (витка) с током, находящегося в вакууме (рис. 3.8). Выделим произвольный бесконечно малый элемент проводника dl и проведем радиус-вектор 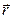в центр витка. Создаваемое элементом тока 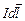магнитное поле в центре витка будет иметь магнитную индукцию 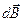, направленную, в соответствии с (3.7), перпендикулярно плоскости витка. Нетрудно понять, что и другие элементы проводника будут создавать в центре витка поле, направленное так же. Поэтому полное поле 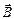(на рис. 3.8 оно изображено кружком с крестиком) в центре витка определится как интеграл от скалярного выражения (3.8):

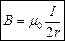, или (3.9)

Магнитная индукция в центре витка пропорциональна току и обратно пропорциональна радиусу витка.

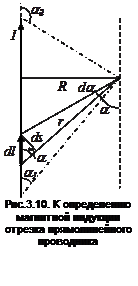
Найдем выражение для магнитной индукции поля, создаваемого отрезком прямолинейного проводника в точке, расположенной на расстоянии R от оси проводника. Из рис.3.10 видно, что 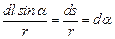, 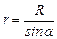. Подставив эти выражения в формулу (3.8), получим: 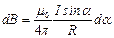. Все элементы dl проводника будут создавать в данной точке элементарные поля одинакового направления (в данном случае от нас перпендикулярно плоскости чертежа). Полное поле отрезка проводника определится путем интегрирования выражения для элементарного поля: 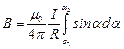. Окончательное выражение имеет вид:

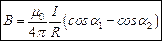(3.11)

В этом выражении углы a₁ и a₂ определяют направления из данной точки на концы проводника. Если длина проводника стремится к бесконечности, то a₁ ® 0, a₂ ® p. При этом выражение (3.11) принимает вид:

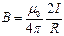(3.12)

На рис. 3.11 изображены магнитные силовые линии прямого проводника с током, имеющие вид концентрических окружностей. Для точки, находящейся на расстоянии R от проводника, показано направление вектора .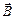

Направление магнитного поля, созданного проводником с током, можно найти с помощью правила буравчика. Для прямолинейного проводника правило применяется следующим образом: если вращать ручку буравчика так, чтобы его поступательное движение совпадало по направлению с током (на рис.3.11 - вверх), то направление движения ручки буравчика будет совпадать с направлением силовых линий. Для кольцевого проводника: если вращать ручку буравчика по направлению тока (по часовой стрелке на рис.3.8), то поступательное движение будет совпадать по направлению с магнитной индукцией в центре витка (на рис. 3.8 - от нас).

Рис. 3.11. Магнитное поле прямолинейного проводника с током

[1] Экспериментальное определение силы в рассматриваемом случае по ряду причин представляет собой непростую задачу.