
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Способ концентрических сфер
|
|
Пример. Построить линию пересечения цилиндра и конуса, оси которых i и f пересекаются в точке О и параллельны плоскости проекций П2 (рисунок 4.5.).
Решение. Проведем из точки О, как из центра, произвольную сферу, пересекающую каждую из данных поверхностей. Сфера будет соосна с данными поверхностями и пересечётся с каждой поверхностью по окружностям. Окружности изобразятся на плоскости проекции П2 отрезками прямых, что следует из параллельности осей данных поверхностей плоскости П2. В пересечении отрезков прямых, изображающих окружности, получим проекции точек, принадлежащих обеим данным поверхностям, а, значит, искомой линии пересечения.
Вначале строятся опорные точки A, B, C, D, которые одновременно являются и точками видимости линии пересечения поверхностей. Эти точки находятся на пересечении контурных образующих данных поверхностей.
Далее определяем радиусы максимальной и минимальной сфер. Радиус максимальной сферы (Rmax) равен расстоянию от проекции центра сфер О2 до наиболее удаленной точки пресечения очерковых образующих (точка А2).
Для определения радиуса минимальной сферы (Rmin) необходимо провести через точку О2 нормали к очерковым образующим данных поверхностей. Больший из отрезков этих нормалей и будет Rmin. Сфера минимального радиуса касается образующих одной из данных поверхностей, а с образующими другой поверхности пресекается. В данном примере сфера минимального радиуса касается образующих цилиндрической поверхности по окружности 1 - 2; коническую поверхность она пересекает по двум окружностям 3 - 4 и 5 - 6. Точки E, F, G,H пересечения этих окружностей принадлежат промежуточным точкам искомой линии пересечения.
Для построения других промежуточных точек необходимо провести ряд концентрических сфер с центром в точке О, причем радиус R этих сфер должен находится в пределах Rmin< R< Rmax.
В данном примере проведена одна дополнительная сфера радиуса R. Она пересекает цилиндрическую поверхность – по окружностям 7 - 8 и 9 - 10, а коническую поверхность – по окружностям 11 - 12 и 13 - 14.
В пресечении этих окружностей получаем точки K,L,M,N,P,Q, принадлежащих линии пересечения.
Для построения горизонтальной проекции точек линии пересечения следует воспользоваться окружностями той или другой из данных поверхностей, содержащими искомые точки. В данном примере применены окружности конической поверхности, т.к. они не искажаются на плоскости проекции П 1.
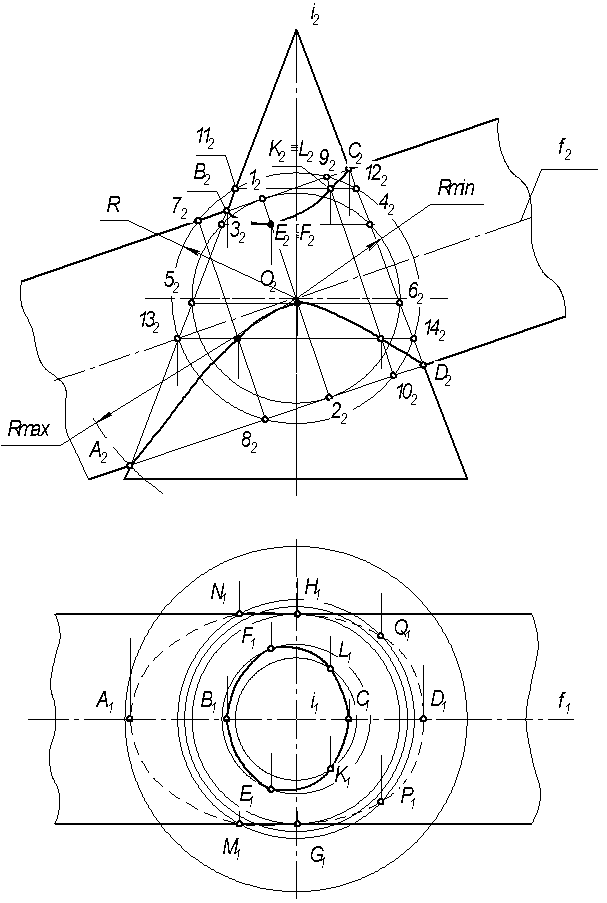
Рисунок 4.5 - Применение способа концентрических сфер
Если оси данных поверхностей вращения пересекаются, но не параллельны какой-либо плоскости проекций, то можно при помощи замены плоскостей проекций привести их в положение, параллельное новой плоскости проекций.
Date: 2015-05-04; view: 888; Нарушение авторских прав