Способ вспомогательных сфер

Способ основывается на построении линии взаимного пересечения каждой из пересекаемых поверхностей вращения с соосно-расположенными сферами.

Поверхности вращения называются соосными, если их оси вращения совпадают. Две соосные поверхности вращения пересекаются по окружностям. Число окружностей равно числу описывающих эти окружности точек пересечения образующих, лежащих в одной меридиональной плоскости и по одну сторону от оси вращения.

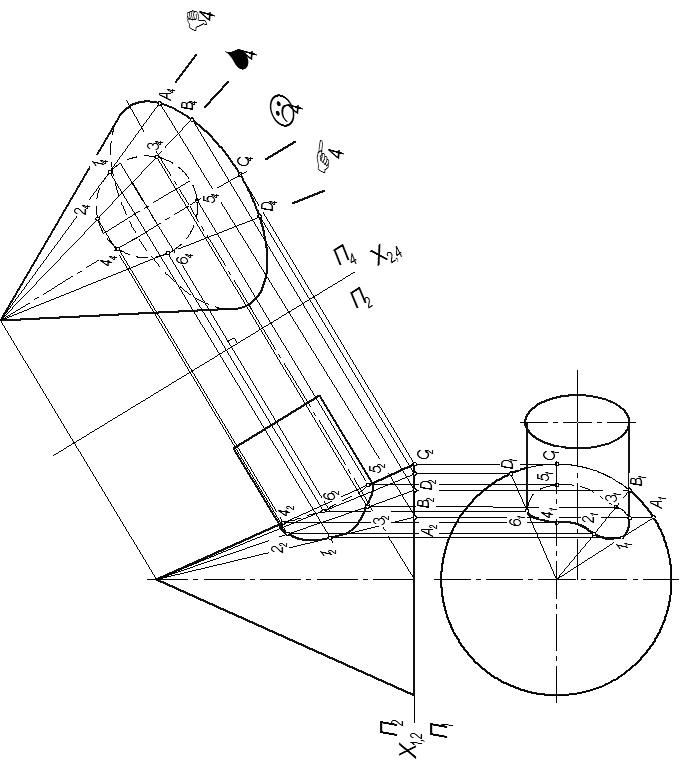
Рисунок 4.3 - Пересечение конуса и цилиндра с скрещивающимися осями

На рисунке 4.4 приведены примеры пересечения со сферой цилиндра и конуса.

Сфера является соосной с данными поверхностями, т.к. центр сферы расположен на оси цилиндра и конуса. Получаемые в пересечении кривые представляют собой окружности, которые проецируют-

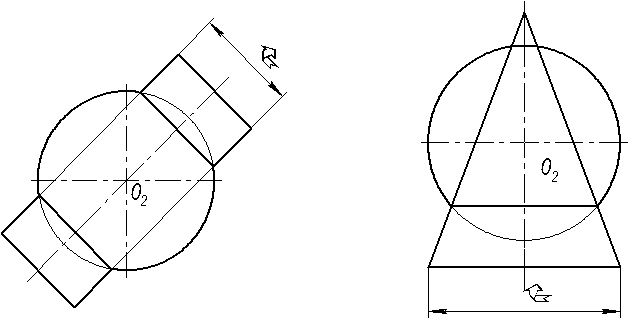
Рисунок 4.4 - Пересечение соосных поверхностей

ся на плоскость, параллельную оси поверхности, в виде отрезков прямых.

С помощью сферических поверхностей просто решаются задачи по определению линий пересечения двух произвольных поверхностей вращения, имеющих общую плоскость симметрии.

При этом возможны два случая:

1)если оси поверхностей пересекаются, то для определения линии пересечения поверхностей используют семейство концентрических сфер;

2)если оси не пересекаются, применяют эксцентрические сферы.

Рассмотрим каждый случай в отдельности.

Date: 2015-05-04; view: 575; Нарушение авторских прав