Абсолютно упругий удар

Лабораторная работа№ 101

(для физиков)

Изучение законов столкновения тел

Принадлежности: прибор для исследования столкновения шаров ЛКТМ-6, набор шаров (стальные, алюминиевые, латунные).

Цель работы:

1. Экспериментальная проверка выполнения закона сохранения импульса при столкновении шаров.

2. Определение экспериментальной зависимости времени соударения шаров от скорости.

3. Определение модуля Юнга

4. Определение средней силы соударения двух шаров.

Введение. В механике, под ударом следует понимать кратковременное взаимодействие двух или более тел, возникающее в результате их соприкосновения.

Абсолютно упругий удар.

Если в результате удара механическая энергия не переходит в другие формы энергии, то удар называется абсолютно упругим. При упругом ударе соударения двух тел, например, двух костяных или стальных твердо закаленных шариков, происходит упругая деформация шариков, поверхности соударяющихся тел вдавливаются и сила давления, вследствие деформации шариков, изменяет их скорость. Анализ явлений, имеющих место при ударе упругих сплошных тел, довольно сложен. Рассмотрим самый простой случай – центральный удар двух однородных шаров. Центральным называют такой удар, при котором скорости соударяющихся шаров до удара совпадают по направлению с линией, соединяющей центры масс шаров (рис 1а). Эта прямая линия называется линией центров. Процесс соударения происходит примерно следующим образом. Во время сближения шаров (рис.1б) силы, действующие на них ( и ), увеличиваются с увеличением деформации, пока скорости обоих шаров не сравняются (рис. 1в). В этот момент деформации достигают максиму - Рис. 1

ма, а затем они начинают умень-

шаться, при этом силы деформации расталкивают шары (рис. 1г) до тех пор, пока они не разойдутся; далее шары будут двигаться с различными скоростями (рис.1д). Вывод выражения для потенциальной энергии сжатия U_сж для двух шаров довольно сложен (впервые получен Г.Герцем)

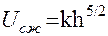,где коэффициент ,

Е- модуль Юнга, коэффициент Пуассона, R-радиус шаров.

Можно довольно просто определить скорости шаров после удара при известных величинах масс шаров и их скоростей до удара, когда нет перехода механической энергии в тепловую. Действительно, в случае абсолютно упругого удара шары при столкновении сплющиваются, и их кинетическая энергия частично переходит в потенциальную энергию упруго деформированных шаров. В этот момент шары аналогичны сжатым пружинам, стремящимся перейти в недеформированное состояние. Ввиду этого начинается обратный процесс перехода энергии упругих деформаций в кинетическую энергию поступательного движения шаров. Когда он заканчивается, шары разлетаются в разные стороны и вновь оказываются не деформированными. Таким образом, кинетическая энергия поступательного движения шаров снова принимает исходное значение, каким оно было до удара. Для реальных тел этот процесс осложняется возникновением упругих возмущений, распространяющихся в шарах со скоростью звука, излучением звуковых волн, а так же внутренним трением и остаточным деформациями. После столкновения часть энергии уноситься в виде энергии таких упругих возмущений, внутренних движений звуковых волн, излученных в окружающую среду. Эта часть энергии в конце переходит в тепловую (внутреннюю) энергию. Она может быть очень малой и в определенном случае идеально упругих шаров обращается в ноль.

Если удар можно считать абсолютно упругим, то для скоростей до и после удара должны быть справедливы уравнения, выражающие закон сохранения импульса и закон сохранения энергии.

(1)

Уравнение (1) в случае центрального удара можно рассматривать как скалярное (все скорость до и после удара направлены по линии центров и их разные направления различаются только знаком) и переписать его в виде

(2)

где υ₁ и υ₂ – скорости шаров до удара, а υ^’₁ и υ^’₂ – скорости их после удара.

Разделив второе уравнение на первое, получим:

(3)

Умножая это уравнение один раз на m ₂, а другой раз на m ₁ и вычитая его из уравнения (2), получим выражение для обеих скоростей после удара:

(4)

В общем виде эти выражения сложны. Мы рассмотрим только два частных случая, охватываемых этими соотношениями.

1) Сумма импульсов обоих шаров до удара равна нулю, т.е.

(5)

Тогда уравнения (4) принимают вид

, ,

Откуда, применяя (5), находим

, ,

т. е. импульсы обоих шаров при ударе только изменяют свой знак. Результат этот почти очевиден. Так как по закону сохранения импульса оба импульса после удара должны быть также равны по величине и противоположны по знаку, а по закону сохранения энергии они при этом не должны изменять своей абсолютной величины, то они могут только изменить знаки на обратное.

2) один шар до удара покоился: υ₂=0. тогда

,

После удара второй шар движется в ту же сторону, куда двигался первый до удара. Скорость υ^’₂ и поведение первого шара зависит от соотношения масс.

а) Если m ₁> m ₂, то первый шар продолжает двигаться в том же направлении, как и до удара, но с меньшей скоростью. Скорость второго шара после удара больше, чем скорость первого до удара (рис. 2).

б) Если m ₁< m ₂, то направление движения первого шара при ударе изменится – шар отскакивает обратно. Второй шар движется в ту сторону, в которую двигался первый до удара, но с меньшей скоростью (рис. 3).

в) Массы шаров одинаковы: m ₁= m ₂. Тогда

,

т.е. шары равной массы при ударе обмениваются скоростями.

Рис. 2. Рис. 3.

Date: 2015-11-15; view: 852; Нарушение авторских прав