
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Розв'язання. Інформаційні втрати в каналі зв'язку визначаються умовною ентропією H(X/Y) одного джерела щодо іншого
|
|
Інформаційні втрати в каналі зв'язку визначаються умовною ентропією H (X / Y) одного джерела щодо іншого.
Для того щоб обчислити повну умовну ентропію H (X / Y), потрібно знайти розподіли безумовних ймовірностей p (xi), p (yj) і побудувати матрицю умовних ймовірностей p (xi / yj).
Безумовний закон розподілу p (xi) знаходимо, виконавши в матриці сумісних ймовірностей p (xi, yj) згортку за j:
p (x 1)= 0,15+0,15+0=0,3, i =1;
p (x 2)= 0+0,25+0,1=0,35, i =2;
p (x 3)= 0+0,2+0,15=0,35, i =3.
Перевіряємо умову нормування
p (x 1) + p (x 2) + p (x 3)=0,3+0,35+0,35=1.
Виходячи з розподілу безумовних ймовірностей д. в. в. X, обчислимо її ентропію:
 (біт / сим).
(біт / сим).
Безумовний закон розподілу p (yj) знаходимо, виконавши в матриці сумісних ймовірностей p (xi, yj) згортку за i:
p (y 1)= 0,15+0+0=0,15, j =1;
p (y 2)= 0,15+0,25+0,2=0,6, j =2;
p (y 3)= 0+0,1+0,15=0,25, j =3.
Перевіряємо умову нормування:
p (y 1) + p (y 2) + p (y 3)=0,15+0,6+0,25=1.
Матрицю умовних ймовірностей знаходимо, скориставшись формулою множення ймовірностей p (xi, yj)= p (yj)× p (xi / yj).
Звідси випливає, що  .
.
Отже, матриця умовних ймовірностей p (xi / yj) знаходиться так:
 .
.
Для матриціумовних ймовірностей p (xi / yj) повинна виконуватися умова нормування
 .
.
Перевіряємо цю умову:
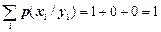 ,
,
 ,
,
 .
.
Скориставшись матрицею умовний ймовірностей p (xi / yj), обчислимо часткові умовні ентропії X стосовно Y:
 (біт/сим);
(біт/сим);
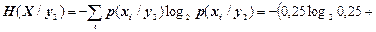
 (біт/сим);
(біт/сим);

 (біт/сим).
(біт/сим).
Виходячи з безумовного закону розподілу д. в. в. Y та знайдених часткових умовних ентропій H ( X/yj ), відшукуємо їх математичне сподівання – загальну умовну ентропію

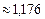 (біт/сим).Отже, інформаційні втрати в каналі зв'язку H (X / Y)»1,18 (біт / сим).
(біт/сим).Отже, інформаційні втрати в каналі зв'язку H (X / Y)»1,18 (біт / сим).
Пропускна здатністьканалу із шумом обчислюється за формулою
 ,
,
де через k позначено об'єм алфавіту джерела; t - час вибору повідомлення джерелом.
Отже, отримаємо  (бод).
(бод).
Кількість переданої по каналу інформації,що припадає на одне повідомлення джерела, знаходиться, виходячи із середньої кількості інформації, що виробляється джерелом – його ентропії і інформаційних втрат в каналі:
I (X, Y)= HX - H (X / Y)=1,581-1,176»0,406 (біт / сим).
Швидкість передачі інформації знаходиться так:
 (бод).
(бод).
Відповідь: H (X / Y)»1,18 (біт /с им); C»409 (бод); v =406 (бод).
Задачі до розділу 2
1 Дослідження каналу зв'язку між джерелом X і спостерігачем Y виявило такі умовні ймовірності вибору повідомлень yjÎY:
 .
.
Знайти часткові H (X / yj) і загальну H (X / Y) умовні ентропії повідомлень у цьому каналі, якщо джерело задане ансамблем { x 1, x 2, x 3 } з ймовірностями { 0,3; 0,2; 0,5 }.
2 Два статистично залежних джерела X та Y визначаються матрицею сумісних ймовірностей
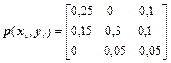 .
.
Знайти часткові й загальну умовні ентропії H (X / yj), H (X / Y) і взаємну інформацію I (X, Y).
3 Два статистично залежних джерела X та Y визначаються матрицею сумісних ймовірностей
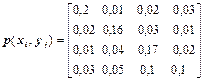 .
.
Знайти часткові й загальну умовні ентропії H (X / yj), H (X / Y) і взаємну інформацію I (X, Y).
4 Матриця сумісних ймовірностей каналу зв'язку має вигляд
 .
.
Знайти часткові й загальну умовні ентропії H (X / yj), H (X / Y) і взаємну інформацію I (X, Y).
5 Дослідження каналу зв'язку між джерелом X і спостерігачем Y виявило такі умовні ймовірності вибору повідомлень yjÎY:
 .
.
Знайти часткові й загальну умовні ентропії повідомлень у цьому каналі H (X / yj), H (X / Y), якщо джерело задане ансамблем { x 1, x 2, x 3 } з ймовірностями { 0,7; 0,2; 0,1 }.
6 Джерело повідомлень X задано ансамблем { x1, x2, x3 } з ймовірностями p (x 1)= 0,65, p (x 2)= 0,25, p (x 3)= 0,1. Матриця умовних ймовірностей каналу має вигляд
 .
.
Знайти кількість інформації, передану в одному й 100 повідомленнях джерела, інформаційні втрати в каналі при передачі 100 повідомлень з алфавіту X?
7 Канал передачі інформації заданий ансамблем { x1, x2, x3 } з ймовірностями { 0,3; 0,2; 0,5 }. Матриця умовних ймовірностей каналу має вигляд
 .
.
Знайти інформаційні втрати в каналі, пропускну здатність каналу й швидкість передачі повідомлень джерелом, якщо час передачі одного повідомлення t =10-3 c.
8 Матриця сумісних ймовірностей каналу зв'язку має вигляд
 .
.
Знайти інформаційні втрати в каналі й швидкість передачі інформації, якщо час передачі одного повідомлення t = 10-3 c.
9 Знайти кількість переданої інформації в одному повідомленні джерела й пропускну здатність каналу зв'язку при t = 10-3 c, де t - час, затрачуваний на передачу одного повідомлення, якщо матриця сумісних ймовірностей каналу має вигляд
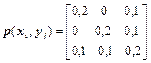 .
.
10 Знайти пропускну здатність каналу зв'язку при t = 10-2 c, де t - час, затрачуваний на передачу одного повідомлення, якщо матриця сумісних ймовірностей каналу має вигляд
 .
.
Чи можлива безпомилкова передача в цьому каналі, якщо продуктивність джерела Vдж = 96 сим/с?
11 Знайти інформаційні втрати в каналі й пропускну здатність дискретного каналу зв'язку при t =10-3 c, де t - час, затрачуваний на передачу одного повідомлення, якщо матриця сумісних ймовірностей каналу має вигляд
 .
.
Чи можлива безпомилкова передача інформації в цьому каналі, якщо продуктивність джерела Vдж = 860 сим / с?
Контрольні запитання до розділів 1-2
1 Які існують види інформації?
2 Як перевести неперервну інформацію в дискретний (цифровий) вигляд?
3 Що таке частота дискретизації неперервної інформації?
4 Як формулюється теорема дискретизації?
5 Що таке інформація, кодування, канал зв'язку, шум?
6 У чому полягають основні положення Шеннона до визначення кількості інформації?
7 Як визначається кількість інформації, що міститься в одному повідомленні дискретного джерела?
8 Як визначається кількість інформації на одне повідомлення джерела взаємозалежних повідомлень?
9 Що таке ентропія джерела? Які її властивості?
10 За яких умов ентропія джерела максимальна?
11 Як визначається кількість інформації? Які властивості кількості інформації?
12 Що таке умовна ентропія?
13 Як описується модель системи передачі інформації?
14 Які є види умовної ентропії?
15 Які основні властивості умовної ентропії?
16 Як знаходиться часткова умовна ентропія?
17 Як знаходиться загальна умовна ентропія?
18 Чим обумовлена статистична надмірність джерела інформації?
19 Чим визначається ентропія об'єднання двох джерел інформації?
20 Які основні властивості взаємної ентропії?
21 Як знаходиться кількість інформації на одне повідомлення двох статистично залежних джерел?
22 Що таке продуктивність джерела інформації?
23 Як визначається швидкість передачі інформації по каналу зв'язку?
24 Чим визначаються інформаційні втрати при передачі інформації по каналу зв'язку?
25 Чим визначаються інформаційні втрати в каналі за відсутності завад?
26 Чим визначаються інформаційні втрати в каналі при великому рівні завад?
27 Чим визначаються інформаційні втрати в каналі за наявності завад?
28 Як знаходиться кількість інформації, передана в одному повідомленні?
29 Чим визначається пропускна спроможність каналу зв'язку?
30 Чим визначається пропускна спроможність каналу зв'язку за відсутності завад?
31 Як формулюється теорема Шеннона про кодування дискретного джерела за відсутності завад?
32 Як формулюється теорема Шеннона про кодування дискретного джерела за наявності завад?
33 Як формулюється зворотна теорема Фано про кодування дискретного джерела за наявності завад?
| Частина II Економне кодування інформації. Статистичні та словникові методи стиснення даних |
Розділ 3 ОПТИМАЛЬНІ СТАТИСТИЧНІ МЕТОДИ СТИСНЕННЯ ІНФОРМАЦІЇ
3.1 Способи задання кодів. Статистичне кодування
Кодування інформації, здійснюване для зменшення надмірності повідомлень, називається економним кодуванням, або стисненням інформації.
Мета стиснення - зменшення кількості бітів, необхідних для зберігання і передачі інформації, що надає можливість передавати повідомлення швидше і зберігати економніше і оперативніше.
Розглянемо приклади кодів і способи їх задання.
Найпростішим способом представлення кодів є кодові таблиці, що зіставляють символам повідомлень певні кодові комбінації. Приклад кодової таблиці подається в табл. 2.1.
Неважко переконатися, що будь-яке повідомлення xi з алфавіту об'ємом k можна закодувати послідовністю кодових символів з набору розміром N=ql комбінацій, де N ³ k, l - довжина кодової комбінації. У загальному випадку  . Наприклад: k =32, q =2, тоді l =5, відповідними двійковими кодовими комбінаціями будуть 00000…11111; k =1000, q =10, тоді l =3, кодові комбінації – 0…999.
. Наприклад: k =32, q =2, тоді l =5, відповідними двійковими кодовими комбінаціями будуть 00000…11111; k =1000, q =10, тоді l =3, кодові комбінації – 0…999.
Основа коду q може бути довільною, проте в комп'ютерних системах передачі і зберігання інформації найбільш поширені двійкові (бінарні) коди.
Таблиця 2.1
| Символ xi | Число

| Код з основою 10 | Код з основою 4 | Код з основою 2 |
| А | ||||
| Б | ||||
| В | ||||
| Г | ||||
| Д | ||||
| Е | ||||
| Ж | ||||
| З |
Наочним і зручним способом задання кодів є їхнє подання у вигляді кодового дерева (рис. 2.1).
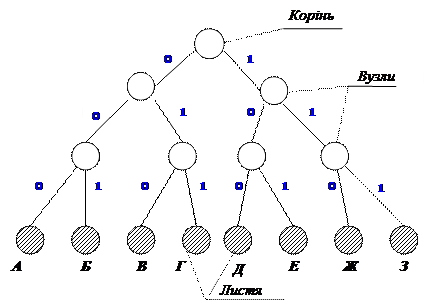
|
Для цього, починаючи з деякої точки - кореня кодового дерева, проводяться гілки, що позначаються 0 або 1. На листях кодового дерева знаходяться символи алфавіту джерела, причому кожному символу відповідає свій лист і свій шлях від кореня до відповідного листа, який утворює певну кодову комбінацію.
Код, поданий кодовим деревом на рис. 2.1, є примітивним рівномірним трирозрядним кодом. Перевага рівномірних кодів, що мають однакову для всіх символів довжину, полягає в простоті кодування/декодування і синхронізації системи (рис. 2.2).
 |
Прикладом нерівномірного коду може бути кодове дерево, зображене на рис. 2.3.
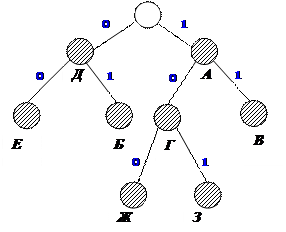 | |||
|
Це приклад непрефіксних кодів. На практиці такі коди не можуть застосовуватися без спеціальних роздільників.
Найбільш поширені нерівномірні коди, що однозначно декодуються. Для цього необхідно, щоб всім символам алфавіту відповідали листя кодового дерева (рис. 2.4), причому жодна кодова комбінація не повинна бути початком (префіксом) іншої, більш довгої, - це префіксні коди.

Задача прийому і декодування нерівномірних кодів набагато складніша, оскільки надходження елементів повідомлення стає неперіодичним (рис.2.5).

Розглянемо приклади кодування повідомлень xi з алфавіту об'ємом k =8 за допомогою l -розрядного двійкового коду.
Приклад 1 Нехай джерело видає одне з 8 повідомлень А...З, що мають однакову імовірність.
Кодування цих повідомлень рівномірним трирозрядним кодом наведено в табл. 2.1. Тоді:
- ентропія джерела  (біт/сим);
(біт/сим);
- надлишковість джерела  ;
;
- середня довжина коду  (біт/сим);
(біт/сим);
- надлишковість коду 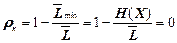 .
.
Отже, при передачі рівноімовірних повідомлень надлишковість рівномірного коду дорівнює нулю, тобто в цьому випадку рівномірне кодування є оптимальним.
Приклад 2 Припустимо, що повідомлення нерівноймовірні (табл. 2.2).
Таблиця 2.2
| А | Б | В | Г | Д | Е | Ж | З |
| 0,6 | 0,2 | 0,1 | 0,04 | 0,025 | 0,015 | 0,01 | 0,01 |
Ентропія джерела при цьому буде менше: Н(Х)» 1,781 (біт/сим).
Середнє число символів на одне повідомлення при використовуванні рівномірного трирозрядного коду  (біт/сим).
(біт/сим).
Надлишковість коду  , тобто має досить велику величину (в середньому 3 символи з 10 не несуть ніякої інформації).
, тобто має досить велику величину (в середньому 3 символи з 10 не несуть ніякої інформації).
Отже, при кодуванні нерівноімовірних повідомлень рівномірні коди характеризуються значною надмірністю. У таких випадках доцільно використовувати нерівномірні коди, довжина кодових комбінацій яких залежить від імовірності символів в повідомленні. Таке кодування називається статистичним. Нерівномірний код при статистичному кодуванні вибирається так, щоб більш імовірні значення передавалися за допомогою більш коротких комбінацій коду, а менш імовірні - за допомогою більш довгих. У результаті зменшується середня довжина коду.
3.2 Елементи теорії префіксних множин
Префіксною множиноюS називається скінченна множина двійкових слів, в якій жодна з послідовностей не є префіксом (початком) ніякої іншої.
Якщо S ={ w 1, w 2, …, wk } – префіксна множина, то можна визначити вектор n (S) =(L 1, L 2, …, Lk), що складається із значень довжин відповідних префіксних послідовностей у неспадному порядку. Цей вектор називається вектором Крафта,для якого виконується нерівність Крафта:
 . (2.1)
. (2.1)
Для вектора Крафта справедливе таке твердження: якщо S - префіксна множина, то n (S) - вектор Крафта.
Якщо нерівність (2.1) переходить в строгу рівність, то такий код називається компактним і має найменшу серед кодів з даним алфавітом довжину, тобто є оптимальним.
Приклади префіксних множин і відповідних їм векторів Крафта: S1={0, 10, 11}® n(S1)=(1, 2, 2); S2={0, 10, 110, 111}® n(S2)=(1, 2, 3, 3); S3={0, 10, 110, 1110, 1111}® n(S3)=(1, 2, 3, 4, 4); S4={0, 10, 1100, 1101, 1110, 1111}® n(S4)={1, 2, 4, 4, 4, 4}; S5={0, 10, 1100, 1101, 1110, 11110, 11111}® n(S5)=(1, 2, 4, 4, 4, 5, 5); S6={0, 10, 1100, 1101, 1110, 11110, 111110, 111111}® n(S6)=(1, 2, 4, 4, 4, 5, 6, 6).
Припустимо, використовується код без пам'яті для стиснення вектора даних x =(x1, x2, …, xn) з алфавітом А об'ємом k символів.
Позначимо через F =(F1, F2, …, Fk) вектор частот символів алфавіту А в повідомленні X.
Кодування повідомлення кодом без пам'яті здійснюється у такий спосіб:
1) складається список символів алфавіту A: a1, a2, …, ak у порядку спадання їх частот появи в X;
2) кожному символу аj призначається кодове слово wj з префіксної множини S двійкових послідовностей, для якої вектор Крафта n (S)=(L1, L2, …, Lk);
3) виходом кодера є об'єднання в одну послідовність усіх отриманих кодових слів.
Тоді довжина кодової послідовності на виході кодера джерела інформації становить
L (X)= L × F = L1 × F1 + L2 × F2 +…+ Lk × Fk. (2.2)
Date: 2015-11-15; view: 1028; Нарушение авторских прав