Комплексные уравнения и векторная диаграмма реального трансформатора

В реальном трансформаторе помимо основного магнитного потока Ф, замыкающегося по магнитопроводу и сцепленного со всеми обмотками трансформатора, имеются также потоки рассеяния Ф_σ1 и Ф_σ2 (рис 1.7), которые сцеплены только с одной из обмоток. Потоки рассеяния не участвуют в передаче энергии, но создают в каждой из обмоток соответствующие ЭДС самоиндукции ; .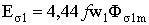

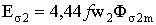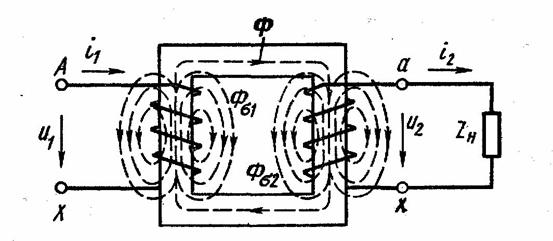
Рис. 1.7

C учетом ЭДС самоиндукции и падений напряжения в активных сопротивлениях обмоток можно составить комплексные уравнения для первичной и вторичной обмоток трансформатора. С учетом (1.13) получим следующую систему уравнений:

(1.17)

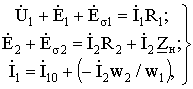
где: 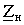- сопротивление нагрузки, подключенной к трансформатору.

Поскольку потоки рассеяния полностью или частично замыкаются по воздуху, они пропорциональны МДС соответствующих обмоток или соответствующим токам:

(1.18)

; .

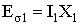Величины X1 и X2 называют индуктивными сопротивлениями обмоток транс-форматора, обусловленными потоками рассеяния. Так как векторы ЭДС Е_σ1 и Е_σ2отстают от соответствующих потоков и токов на 90°, то

(1.19)

; .

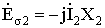При этом комплексные уравнения трансформатора примут вид

(1.20)

;

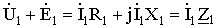(1.21)

;

(1.22)

.

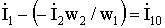Замена ЭДС 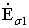и падениями напряжений j Í₁ X₁ и j Í₁ X₂ наглядно показывает роль потоков рассеяния: они создают индуктивные падения напряжения в обмотках, не участвуя в передаче энергии из одной обмотки в другую. Проще становится и построение векторной диаграммы, соответствующей системе уравнений (1.20) – (1.22), в которой целесообразно также заменить падение напряжения в нагрузке величиной 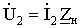, т.е. вторичным напряжением трансформатора, определяемым из (1.21):

(1.23)

.

Векторную диаграмму вторичной обмотки трансформатора (рис. 1.8, а) строят согласно уравнению (1.23). Характер диаграммы определяется током нагрузки Í₂, который принимается заданным по величине и фазе. Иными словами, задаваясь векторами вторичного тока Í₂ и напряжения Ú₂, можно построить вектор ЭДС

(1.24)

,

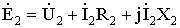если известны параметры трансформатора. Вектор Í₂ R₂ параллелен вектору тока Í₂, a вектор j Í₂ X₂ опережает вектор тока Í₂ на угол 90°. На диаграмме изображен и вектор магнитного потока 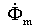, который опережает вектор ЭДС É₂ на 90°. Векторную диаграмму первичной обмотки трансформатора (рис. 1.8, б) строят в соответствии с уравнением

(1.25)

.

Построение диаграммы начинают с вектора потока 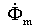, который создается током холостого хода Í₁₀. Этот ток опережает вектор потока 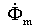на угол 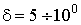. Вектор ЭДС É₁, как и É₂, отстает от потока 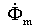на угол 90°.

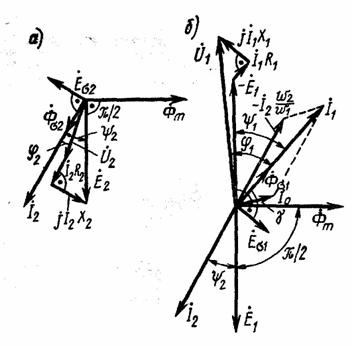
Рис. 1.8

Ток в первичной обмотке трансформатора 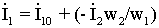, поэтому на рис.1.8,б нужно показать и вектор тока Í₂, сдвинутый на угол ψ₂ относительно вектора É₁ (векторы É₁ и É₂ совпадают по направлению). Зная Í₂, можно изобразить вектор 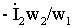и получить вектор Í₁ как сумму векторов Í₁₀ и .

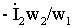Найдя вектор тока Í₁, можно определить значения векторов Í₁ R₁ и j Í₁ X₁ и построить искомый вектор напряжения Ú₁ как сумму трех составляющих: векторов -É₁ и падений напряжений в обмотках Í₁ R₁ и j Í₁ X₁.

Date: 2015-11-15; view: 354; Нарушение авторских прав