
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Розділ 8. Генетичні процеси у популяціях
|
|
Кожна популяція особин, що входить до складу біологічного вида, має специфічну генетичну структуру, яка характеризується:
1) генофондом – сукупністю генів, поширених у популяції з певною частотою;
2) частотами поширеності різних генотипів, утворених внаслідок комбінацій цих генів.
Мінливість генофонду менделівської популяції є основою еволюції виду.
Менделівська популяція – сукупність у певному ступені подібних за генотипом і фенотипом особин, що заселяють певний ареал, характеризуються однаковим способом розмноження, однаковою спадковою мінливістю і підлягають дії добору та зовнішнього середовища. Це поняття поширюється тільки на сукупність організмів, що вільно схрещуються та перехресно запліднюються. Популяції самозапильних (або тих, що самозапліднюються) форм є сукупністю чистих ліній.
Генетична структура ідеальних менделівських популяцій залишається незмінною протягом багатьох поколінь і є моделлю для вивчення процесів, що відбуваються в панміктичних популяціях у реальних умовах при накопиченні в ній мутацій, здійсненні міграцій, при обмеженні панміксії, дії різних форм добору.
Популяційна генетика вивчає закономірності змін генетичної структури популяцій з часом під впливом мінливих умов довкілля, що лежать в основі мікроеволюційних процесів.
Панміктичні (з випадковим, вільним схрещуванням особин) популяції, як правило, знаходяться у стані рівноваги та характеризуються певним співвідношенням генотипів, встановленим Дж.Харді та В. Вайнбергом.
Закон Харді-Вайнберга (закон рівноваги генних частот у панміктичній популяції): у присутності альтернативних алелів і при однаковій життєздатності різних генотипів вихідне співвідношення алелів (незалежно від їхньої абсолютної частоти) зберігається в усіх наступних поколіннях (тобто зберігається популяційна рівновага).
При частоті алеля А, яка дорівнює р, частота q алеля дорівнює 1-р. При вільному схрещуванні частота генотипів від рівноймовірного сполучення різних типів гамет, що несуть ці алелі, дорівнюватиме:
(рА+qа)2 = р2АА + 2рqАа + q2аа
| Яйцеклітини | спермії | |
| pA | qa | |
| pA | p2AA | pqAa |
| qa | pqAa | q2aa |
Сума частот генів однієї алельної пари в даній популяції є величиною постійною: 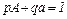
Частоти генів виражають у частках одиниці або у відсотках, тоді:

Цей закон справедливий лише для ідеальних «менделівських» популяцій, які відповідають таким умовам: вільна панміксія (схрещування), відсутність появи нових генів за рахунок міграцій і мутацій, відсутність відтоку генів за рахунок добору, однакова плодючість гомозигот і гетерозигот, повна ізоляція даної популяції, велика чисельність особин.
Отже, закон Харді-Вайнберга виражає ймовірні розподілення генотипів у популяції, що вільно схрещується, у відповідності з коефіцієнтом розкладу бінома Ньютона (р+q)2.
З умовними припущеннями закон Харді-Вайнберга використовується для прогнозування кількісних співвідношень особин з різними генотипами або для визначення поширеності алелів певного гена серед особин даної популяції. Такі прогнози знаходять практичне використання в екології, селекції, медицині.
Date: 2015-11-14; view: 586; Нарушение авторских прав