
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Задача6
|
|
Задачи
Задача 1.
Прогнозування динаміки ВВП
За даними наведеної таблиці розрахувати:
а) дефлятор ВВП у прогнозованому періоді;
б) номінальний та реальний ВВП у прогнозованому періоді.
Таблиця
| Періоди | Номінальний ВВП GDPtn | Реальний ВВП GDPtr | Дефлятор DefGDPt | Індекс спожив-чих цін CPIt | Індекс оптових цін PPIt | Індекс фізичного обсягу ВВП PFIt | Коеф-т впливу оптових цін на ВВП Kt1 |
| 2014 кв1 t1 | |||||||
| кв2 t2 | |||||||
| кв3 t3 | |||||||
| кв4 t4 | |||||||
| 2015 кв1 t5 | 121,3 | 135,5 | 0,950 | 0,324 | |||
| кв2 t6 | 125,5 | 137,7 | 0,983 | 0,418 | |||
| кв3 t7 | 128,1 | 137,1 | 1,001 | -0,213 | |||
| кв1 t8 | 118,3 | 117,7 | 1,020 | 2,167 |
Задача 2.
За даними 30 місяців заданого часового ряду уt були одержані значення
коефіцієнтів автокореляції рівнів:
r1 = 0,63; r2 = 0,38; r3 = 0,72; r4 = 0,97; r5 = 0,55;
r6 = 0,40; r7 = 0,65;
ri - коефіцієнти автокореляції i – го порядку.
а) Охарактеризувати структуру цього ряду, використовуючи графічне відображення коефіцієнтів автокореляції.
б) Для прогнозування майбутніх значень уt пропонується побудувати авторегресійну модель. Обрати найкраще рівняння авторегресії, обґрунтувати вибір. Записати загальний вид цього рівняння.
Задача 3.
Відомі наступні значення рівнів безробіття у, (%) за 8 місяців:
Місяць …. 1 2 3 4 5 6 7 8
yt ………. 8,8 8,6 8,4 8,1 7,9 7,6 7,4 7,0
а) Визначити, до якого класу належить даний динамічний ряд (стаціонарний або нестаціонарний). У разі нестаціонарності сформувати стаціонарний ряд;
б) Записати загальний вид авторегресійної моделі прогнозування, якщо відомі коефіцієнти автокореляції: r1 = - 0,63246; r2 = 0,76376; r3 = - 0,52223;
в) Розрахувати прогноз рівня безробіття на 9-й місяць за допомогою автокореляційної моделі, якщо за оцінкою МНК встановлено її параметри: a0 = 0,4; a1= -1,0; a2= 3,5/
Задача 4.
На основі статистичних даних за період 2001-2014 рр., побудовані регресійні
моделі динаміки валового внутрішнього продукту країни:
лінійна функція  = a+ b×t;
= a+ b×t; 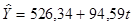
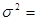 32,6; R2 = 0,965; F =276,88 (Fтабл = 4,96)
32,6; R2 = 0,965; F =276,88 (Fтабл = 4,96)
експоненційна функція  = a × e,bt; Ln
= a × e,bt; Ln 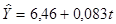 .
.
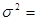 0,06; R2 = 0,9952; F =2057,9 (Fтабл = 4,96)
0,06; R2 = 0,9952; F =2057,9 (Fтабл = 4,96)
1) Визначити за якою функцією оцінка тренду буде кращою.
2) На основі обраної моделі зробити прогноз ВВП на 2015 рік.
Задача 5.
На основі щоквартальних спостережень рівня безробіття в південному
регіоні країни (% від економічно активного населення) за останні 5 років
була побудована мультиплікативна модель часового ряду. Відкориговані
значення сезонної компоненти за кожний квартал наведені нижче:
I квартал.....1,4 III квартал....0,7
II квартал....0,8 IV квартал.....?
Рівняння тренду виглядає наступним чином:
T = 9,2 - 0,3t
(у розрахунку параметрів тренду для нумерації кварталів використовувалися натуральні числа t = 1,2,3,…,20).
1) Визначити значення сезонної компоненти за IV квартал.
2) На основі побудованої моделі розрахувати точкові прогнози рівня безробіття на I і II квартали наступного року.
Задача6.
За даними наведеної таблиці 5, користуючись адитивною моделлю декомпозиційного аналізу часових рядів, розрахувати:
1) сезонну компоненту часового ряду (S);
2) помилку прогнозу (Е), якщо відомі сезонна компонента (S) та рівняння тренду: Y = 15,1451 - 0,2714t;
3) середнє абсолютне відхилення (МАЕ) та середню квадратичну помилку (МSЕ).
Таблиця 5.
| Квартал | t | БВ | Разом за 4кв. | Ковзкі середні |
| 1 | 2 | 3 | 4 | 5 |
| Січень-Березень 19Х6 | 10,200 | |||
| 80,500 | 20,125 | |||
| Квітень-Червень | 22,000 | |||
| 87,000 | 21,75 | |||
| Липень-Вересень | 39,100 | |||
| 83,900 | 20,975 | |||
| Жовтень-Грудень | 15,700 | |||
| 61,900 | 15,475 | |||
| Січень-Березень 19Х7 | 7,100 | |||
| 38,900 | 9,725 | |||
| Квітень-Червень | 7,600 | |||
| 30,600 | 7,65 | |||
| Липень-Вересень | 8,500 | |||
| 27,200 | 6,8 | |||
| Жовтень-Грудень | 7,400 | |||
| 19,600 | 4,9 | |||
| Січень-Березень 19Х8 | 3,700 | |||
| Квітень-Червень | 5,200 |
Date: 2015-11-14; view: 289; Нарушение авторских прав