Постановка зaдaчи линейного программирования

В последние годы мы особенно отчетливо ощутили, что нет ничего важнее для общества, чем здоровая экономика Научное исследование основ функционирования экономики - сложная и интересная деятельность. Математические методы в ней играют возрастающую с каждым десятилетием роль, а реализация возникающих при этом математических моделей и получение практически важных результатов невозможны без ЭВМ.

В данном параграфе рассматривается лишь один из разделов - оптимальное планирование - и внутри него одна из моделей, так называемое, линейное программирование. Это связано с относительной простотой и ясностью как содержательной постановки соответствующих задач, так и методов решения. О таких интересных, но более сложных проблемах, как выпуклое программирование, динамическое программирование, теория игр мы лишь упомянем, отсылая читателей за подробностями к специальной литературе. Отметим еще, что термин «программирование» в названии этих разделов теории оптимального планирования весьма условен, связан с историческими обстоятельствами и к программированию в общепринятом сейчас смысле прямого отношения не имеет.

Общеизвестно, сколь важно для решения экономических задач планирование -как при рыночной, так и при плановой экономике. Обычно для решения экономической проблемы существует много способов (стратегий), отнюдь не равноценных по затратам финансов, людских ресурсов, времени исполнения, а также по достигаемым результатам. Наилучший из способов (по отношению к выбранному критерию - одному или нескольким) называют оптимальным. Приведем простейший пример такого рода задач.

Пример 1. На некотором предприятии могут выпускать изделия двух видов (например, мотоциклы и велосипеды). В силу ограниченности возможностей сборочного цеха в нем могут собирать за день либо 25 мотоциклов (если не собирать вообще велосипеды), либо 100 велосипедов (если не собирать вообще мотоциклы), либо какую-нибудь комбинацию тех и других, определяемою приемлемыми трудозатратами. Склад может принять не более 70 изделий любого вида в сутки. Известно, что мотоцикл стоит в 2 раза дороже велосипеда. Требуется найти такой план выпуска продукции, который обеспечил бы предприятию наибольшею выручку.

Такого рода задачи возникают повседневно в огромном количестве, но в реальности число изделий гораздо больше двух, да и дополнительных условий тоже больше. Решить подобную задачу путем перебора всех мыслимых вариантов часто невозможно даже на ЭВМ. В нашем примере, однако, в ЭВМ нет необходимости -задача решается очень легко.

Обозначим число выпускаемых за день мотоциклов х, велосипедов - у. Пусть τ₁ -время (в часах), уходящее на производство одного мотоцикла, а τ₂ - одного велосипеда. Из условия задачи следует, что τ₁ = 4 τ₂. Если завод работает круглосуточно, то, очевидно, при одновременном выпуске обоих изделий

Но 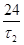- число максимально производимых велосипедов, равное 100. Итак, возможности производства определяют условие

4 x + y ≤ 100 .

x + y ≤ 70

S = а₁ ∙ х + a₂ ∙ у = 2 a₂ ∙ х + а₂ ∙ у = а₂ ∙ ( 2 х + у).

 

Поскольку a₂ - заданная положительная константа, то наибольшего значения следует добиваться отвеличины f = 2х + у.

Итак, учитывая все условия задачи, приходим к ее математической модели: среди неотрицательных целочисленных решений системы линейных неравенств

 

(7.71)

 

найти такое, которое соответствует максимуму линейной функции

 

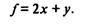(7.72)

 

Проще всего решить эту задачу чисто геометрически. Построим на плоскости (х, у) область, соответствующую неравенствам (7.71) и условию неотрицательности x и у. Эта область выделена на рис. 7.62 жирной линией. Всякая ее точка удовлетворяет неравенствам (7.71) и неотрицательности переменных. Пунктирные линии на рисунке - семейство прямых, удовлетворяющих уравнению f = 2х + у = с (с разными значениями константы с). Вполне очевидно, что наибольшему возможному значению f, совместному с предыдущими условиями, соответствует жирная пунктирная линия, соприкасающаяся с областью М в точке Р.

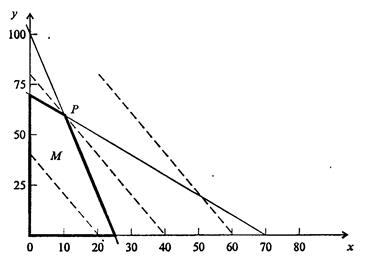
Рис. 7.62. Графическое решение задачи об оптимальном плане производства (к примеру 1)

 

Этой линии соответствует значение f = 80. Пунктирная линия правее хоть и соответствует большему значению f, но не имеет общих точек с М, левее - меньшим значениям f. Координаты точки Р (10, 60) - искомый оптимальный план производства.

Отметим, что нам «повезло» - решение (х, у) оказалось целочисленным. Если бы прямые

4x + y = 100

х + у = 70

пересеклись в точке с нецелочисленными координатами, мы бы столкнулись со значительными проблемами. Еще больше их было бы, если бы наш завод выпускал три и более видов продукции.

Прежде чем обсуждать возникающие при этом математические проблемы, дадим формулировки нескольких классических задач линейного программирования в общем виде.

Пример 2. Транспортная задача. Некий продукт (например, сталь) вырабатывается на т заводах P₁, P₂,..., Р_m, причем ежемесячная выработка составляетдь а₁, a₂, …, а_m тонн, соответственно. Пусть эту сталь надо доставить на предприятия Q₁, Q₂,..., Qk (всего k), причем b₁, b₂,..., b_k - ежемесячная потребность этих предприятий. Наконец, пусть задана стоимость c_ij перевозки одной тонны стали с завода Р_i на предприятие Q_j,. Естественно считать, что общее производство стали равно суммарной потребности вней:

a₁ + a₂ +…+a_m = b₁ + b₂ +…+b_k (7.73)

 

Необходимо составить план перевозок, при котором

1) была бы точно удовлетворена потребность в стали предприятий Q₁, Q₂,..., Q_k,

2) была бы вывезена вся сталь с заводов Р₁, Р₂,....,P_m;

3) общая стоимость перевозок была бы наименьшей.

Обозначим через x_ij количество стали (в тоннах), предназначенной к отправке с завода Р_i на предприятие Q_j. План перевозок состоит из (m∙k) неотрицательных чисел x_ij (i= 1, 2,..., m;j = 1,2,..., k).

Таблица 7.10

Date: 2015-11-13; view: 517; Нарушение авторских прав