Относительность движения. Система отсчёта. Материальная точка. Основные единицы измерения механических величин в СИ

Механика.

Относительность движения- это перемещение и скорость тела относительно разных систем отсчета различны (например, человек и поезд). Скорость тела относительно неподвижной системы координат равна геометрической сумме скоростей тела. Система отсчёта — это совокупность тела отсчёта, связанной с ним системы координат и системы отсчёта времени, по отношению к которым рассматривается движение каких-либо материальных точек или тел. Материальная точка- это физическое тела размерами которого в задаче можно пренебречь. Основные единицы измерения механических величин в СИ- для механики приняты: единица длины - метр (м), единица массы - килограмм (кг), единица времени - секунда (с).
Дополнительными единицами СИ являются: радиан - единица плоского угла СИ и стерадиан — единица телесного угла СИ.
Производные единицы СИ образуются из основных, дополнительных и ранее образованных производных единиц СИ.

2. Естественный способ описания движения материальной точки (скорость, касательное и нормальное ускорение материальной точки, радиус кривизны траектории). Естественный способ описания движения материальной точки. Применяется, если траектория материальной точки известна заранее. На заданной траектории выбирают начало отсчёта -неподвижную точку, а положение материальной точки определяют при помощи дуговой координаты, представляющей собой расстояние вдоль траектории от выбранного начала отсчета до самой материальной точки.
Движение тела считается определённым, если известны его траектория, начало отсчета, положительное направление дуговой координаты и зависимость времени от этой координаты.

3. Поступательное движение твёрдого тела. Траектории, скорости и ускорения точек тела, движущегося поступательно. Поступательное движение твердого тела – это движение, при котором любая прямая, связанная с телом, при его движении остается параллельной своему начальному положению. Примеры поступательного движения: движение педалей велосипеда относительно его рамы, движение поршней в цилиндрах двигателя внутреннего сгорания относительно цилиндров, движение кабин колеса обозрения относительно Земли. Теорема. При поступательном движении твердого тела траектории, скорости и ускорения точек тела одинаковы.

4. Вращательное движение твёрдого тела вокруг неподвижной оси. Уравнение вращательного движения. Угловая скорость и угловое ускорение. Вращательное движение – это движение твердого тела, имеющего как минимум две неподвижные точки. Прямая, проходящая через эти точки, называется осью вращения. Положение тела определено, если задан угол φ между плоскостями П₀ и П, одна из которых неподвижна, а другая жестко связана с телом. φ=φ(t) – уравнение вращательного движения твердого тела. В технике угловая скорость – это частота вращения, выраженная в оборотах в минуту. За одну минуту тело повернется на угол 2π⋅ n, где n – число оборотов в минуту (об/мин). Разделив этот угол на число секунд в минуте, получим. Угловое ускорение – мера изменения угловой скорости:

5. Векторы угловой скорости и углового ускорения. Связь линейных и угловых скоростей и ускорений точек тела, вращающегося вокруг неподвижной оси. Угловое ускорение - аксиальный вектор, определяемый как производная по времени от угловой скорости

Угловая скорость всегда является аксиальным вектором, поскольку построена и малых поворотов d j. При вращении вокруг неподвижной оси угловая скорость не меняет своего направления. При равномерном вращении остается постоянной и ее величина (w = const). В этом случае вращение можно охарактеризовать его периодом Т:

Связь угловых и линейных скоростей и ускорений.Каждая из точек вращающегося тела движется с определенной линейной скоростью v, направленной по касательной к соответствующей окружности. Пусть материальная точка вращается вокруг оси 00' по окружности радиусом R. За малый промежуток времени Dt она пройдет путь Ds, соответствующий углу поворота Dj.

6. Дальнодействие. Закон инерции (первый закон Ньютона). ИСО. Согласно концепции дальнодействия, тела действуют друг на друга без материальных посредников, через пустоту, на любом расстоянии. Такое взаимодействие осуществляется с бесконечно большой скоростью (но подчиняется определённым законам). Примером силы, считавшейся одним из примеров непосредственного действия на расстоянии, можно считать силу всемирного тяготения в классической теории гравитации Ньютона.Закон инерции (первый закон Ньютона)- Всякое тело находится в состоянии покоя или прямолинейном движении пока воздействие других тал не заставит изменить его состояние. ИСО-система отсчёта относительно которой тело движется прямолинейно и равноускоренно. Земля не является ИСО т.к. она движется по окружности.

7. Основные понятия динамики материальной точки (сила, масса, импульс). Второй закон Ньютона- если тело движется с ускорением то равнодействующая равна произведению массы на его ускорение. F- это мера воздействия взаимодействия в результате которого тело или изменяет свою форму или скорость. M- мера инерциальности отзывчивости на воздействие. Масса это агетивная величина. Р- Импульс это физическая величина являющаяся мерой механического движения.

8. Третий закон Ньютона. Границы применимости классической механики. Третий закон Ньютона- выполняется в ИСО значит любое действие носит характер взаимодействия сила с которой действует друг на друга F₁₂=-F₂₁. Релятивистская механика. Переход когда тело приближается к скорости света. Когда в системе очень много частиц.

9. Неинерциальные системы отсчёта (НИСО). Силы инерции в поступательно движущихся НИСО. Неинерциальная система отсчёта — система отсчёта, в которой не выполняется первый закон Ньютона — «закон инерции», говорящий о том, что каждое тело, в отсутствие действующих на него сил, покоится либо движется по прямой и с постоянной скоростью. Всякая система отсчета, движущаяся с ускорением или поворачивающаяся относительно инерциальной, является неинерциальной. Второй закон Ньютона также не выполняется в неинерциальных системах отсчёта. Для того, чтобы уравнение движения материальной точки в неинерциальной системе отсчёта по форме совпадало с уравнением второго закона Ньютона, дополнительно к «обычным» силам, действующим в инерциальных системах, вводят силы инерции. Законы Ньютона выполняются только в инерциальных системах отсчёта. Формулы корил. Центробеж.

10. Силы инерции в равномерно вращающихся НИСО. Центробежная сила инерции. Центробежная сила — составляющая фиктивных сил инерции, которую вводят при переходе из инерциальной системы отсчёта в соответствующим образом вращающуюся неинерциальную. Это позволяет в полученной неинерциальной системе отсчёта продолжать применять законы Ньютона для расчёта ускорения тел через баланс сил.

11. Силы инерции в равномерно вращающихся НИСО. Сила Кориолиса. Сила Кориолиса — одна из сил инерции, существующая в неинерциальной системе отсчёта из-за вращения и законов инерции, проявляющаяся при движении в направлении под углом к оси вращения. Причина появления силы Кориолиса —В инерциальных системах отсчёта действует закон инерции, то есть, каждое тело стремится двигаться по прямой и с постоянной скоростью. Если рассмотреть движение тела, равномерное вдоль некоторого вращающегося радиуса и направленное от центра, то станет ясно, что чтобы оно осуществилось требуется придавать телу ускорение, так как чем дальше от центра, тем должна быть больше касательная скорость вращения. Это значит, что с точки зрения вращающейся системы отсчёта, некая сила будет пытаться сместить тело с радиуса.

12. Механическая система. Внешние и внутренние силы. ЗСИ и его связь с однородностью пространства. Совокупность тел выделенная для рассмотрения называется механической системой. Внешняя сила — это мера взаимодействия между телами. Внутренние силы - это такие силы, которые действуют сразу на все атомы передвигаемого предмета независимо от того, где они находятся: на поверхности или в середине предмета. К этим силам относятся силы инерции и силы поля: гравитационного, электрического, магнитного. Закон сохранения импульса это векторная сумма импульсов всех тел системы есть величина постоянная, если векторная сумма внешних сил, действующих на систему, равна нулю. В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Из законов Ньютона можно показать, что при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил. Согласно теореме Нётер каждому закону сохранения ставится в соответствие некая симметрия уравнений, описывающих систему. В частности, закон сохранения импульса эквивалентен однородности пространства, то есть независимости всех законов, описывающих систему, от положения системы в пространстве. Простейший вывод этого утверждения основан на применении лагранжева подхода к описанию системы.

13. Центр масс механической системы, твёрдого тела. Теорема о движении центра масс. Лабораторная система отсчёта (л -система) и система центра масс(ц -система). Движение твёрдого тела можно рассматривать как суперпозицию движения центра масс и вращательного движения тела вокруг его центра масс. Центр масс при этом движется так же, как двигалось бы тело с такой же массой, но бесконечно малыми размерами (материальная точка). Последнее означает, в частности, что для описания этого движения применимы все законы Ньютона. Во многих случаях можно вообще не учитывать размеры и форму тела и рассматривать только движение его центра масс. Теорема о движении центра масс системы — одна из общих теорем динамики, является следствием законов Ньютона. Утверждает, что ускорение центра масс механической системы не зависит от внутренних сил, действующих на тела системы, и связывает это ускорение с внешними силами, действующими на систему

Часто бывает удобно рассматривать движение замкнутой системы в системе отсчёта, связанной с центром масс. Такая система отсчёта называется системой центра масс (Ц-система), или системой центра инерции. В ней полный импульс замкнутой системы всегда остаётся равным нулю, что позволяет упростить уравнения её движения.

14. Момент силы относительно точки и относительно оси. Пара сил. Момент силы относительно точки О - это вектор, модуль которого равен произведению модуля силы на плечо - кратчайшее расстояние от точки О до линии действия силы. Направление вектора момента силы перпендикулярно плоскости, проходящей через точку и линию действия силы, так, что глядя по направлению вектора момента, вращение, совершаемое силой вокруг точки О, происходит по часовой стрелке. Если известен радиус-вектор r ⃗ точки приложения силы F ⃗ относительно точки О, то момент этой силы относительно О выражается следующим образом: M ⃗ O (F ⃗)= r ⃗ × F ⃗. Пара сил — совокупность двух сил, которые приложены к одному абсолютно твёрдому телу и при этом равны по модулю и противоположны по направлению. Пара сил представляет собой важный частный случай системы сил. Главным вектором для неё служит нулевой вектор, так что действие пары сил на тело полностью характеризуется её главным моментом, который является свободным вектором (не зависит от выбора полюса) и называется моментом пары сил.

15. Момент импульса относительно точки и относительно оси. Связь между моментом силы и моментом импульса (уравнение моментов). Закон сохранения момента импульса и его связь с изотропией пространства. Движение материальной точки в центральном поле. Кроме момента инерции для динамики твердого тела важны момент силы и момент импульса. Если сопоставлять движение твердого тела и движение материальной точки эти моменты являются близкими аналогами силы и импульса.

По определению, моментом силы относительно неподвижной точки о является векторная величина – векторное произведение радиус-вектора, проведенного из рассматриваемой точки о в точку приложения силы b, на вектор силы, т.е. 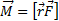. Аналогичным образом определяется момент импульса, .

16. Работа переменной силы. Мощность. Р=А/t.

17. Кинетическая энергия частицы. Теорема об изменении кинетической энергии. Консервативные и неконсервативные силы. Теорема о кинетической энергии системы — одна из общих теорем динамики, является следствием законов Ньютона. Связывает кинетическую энергию механической системы с работой сил, действующих на тела, составляющие систему. В качестве системы, о которой идёт речь, может выступать любая механическая система, состоящая из любых тел. В физике консервативные силы (потенциальные силы) — это силы, работа которых не зависит от вида траектории, точки приложения этих сил и закона их движения, и определяется только начальным и конечным положением этой точки. Равносильным определением является и следующее: консервативные силы — это такие силы, работа которых по любой замкнутой траектории равна 0. Существуют силы, работа которых зависит от формы пути, т. е. работа по замкнутой траектории не равна нулю (например силы трения). Такие силы называют неконсервативными.
В этом случае работа не идёт на увеличение потенциальной энергии (dA dE_n), а идёт на нагревание тел, т. е. на увеличение кинетической энергии молекул тела. Кинетическая энергия тела уменьшается, происходит её рассеяние или диссипация. Однако это не означает, что энергия исчезла. Она просто перешла в энергию теплового движения молекул. Возможен и переход энергии в другие виды, но полный баланс энергии всегда сохраняется.

Date: 2015-11-13; view: 1035; Нарушение авторских прав