Потенциал и энергия электростатического поля. Эквипотенциальные поверхности

Потенциал является энергетической характеристикой поля. Он численно равен работе, которую надо затратить против сил электрического поля при перенесении единичного положительного точечного заряда из бесконечности в данную точку поля. Единица измерения потенциала – вольт.

Когда поле образовано несколькими произвольно расположенными зарядами, потенциал его в данной точке равен алгебраической сумме потенциалов, создаваемых каждым зарядом в отдельности, т.е.

Потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.

Потенциал φ∞ поля точечного заряда Q на расстоянии r от него относительно бесконечно удаленной точки вычисляется следующим образом:

Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью или поверхностью равного потенциала.

Силовые линии электростатическое поля всегда перпендикулярны эквипотенциальным поверхностям.

Эквипотенциальные поверхности кулоновского поля точечного заряда – концентрические сферы.

Эквипотенциальные поверхности и силовые линии простых электрических полей: a – точечный заряд; b – электрический диполь; c – два равных положительных заряда.

При перемещении электрических зарядов силы кулоновского взаимодействия совершают определенную работу dА. Работа, совершенная системой, определяется убылью энергии взаимодействия -dW зарядов

dA = -dW

Энергия взаимодействия двух точечных зарядов q1 и q2, находящихся на расстоянии r₁₂, численно равна работе по перемещению заряда q₂ в поле неподвижного заряда q₁ из точки с потенциалом в точку с потенциалом

энергия системы n зарядов равна:

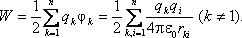
Данная формула справедлива лишь в случае, если расстояние между зарядами заметно превосходит размеры самих зарядов.

4.Работа в электростатическом поле. Работа по замкнутому контуру. Циркуляция .

Электростатическое поле обладает важным свойством:

Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.

Следствием независимости работы от формы траектории является следующее утверждение:

Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю.

На рисунке изображены силовые линии кулоновского поля точечного заряда Q и две различные траектории перемещения пробного заряда q из начальной точки (1) в конечную точку (2). На одной из траекторий выделено малое перемещение ∆ 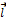. Работа ΔA кулоновских сил на этом перемещении равна:

Таким образом, работа на малом перемещении зависит только от расстояния r между зарядами и его изменения Δr. Если это выражение проинтегрировать на интервале от r = r1 до r = r2, то можно получить:

Полученный результат не зависит от формы траектории. На траекториях I и II, изображенных на рис. 1.4.2, работы кулоновских сил одинаковы. Если на одной из траекторий изменить направление перемещения заряда q на противоположное, то работа изменит знак. Отсюда следует, что на замкнутой траектории работа кулоновских сил равна нулю.

Если электростатическое поле создается совокупностью точечных зарядов 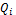то при перемещении пробного заряда q работа A результирующего поля в соответствии с принципом суперпозиции будет складываться из работ кулоновских полей точечных зарядов:

Циркуляцией вектора напряженности называется работа, которую совершают электрические силы при перемещении единичного положительного заряда по замкнутому пути L

Так как работа сил электростатического поля по замкнутому контуру равна нулю (работа сил потенциального поля), следовательно циркуляция напряженности электростатического поля по замкнутому контуру равна нулю.

5. Связь между энергией и силой Кулона, напряжённостью и потенциалом.

Каждой точке потенциального поля соответствует, с одной стороны, некоторое значение вектора силы, действующей на тело, и, с другой стороны, некоторое значение потенциальной энергии. Следовательно, между силой и потенциальной энергией должна существовать определенная связь.

Для установления этой связи вычислим элементарную работу ∆A, совершаемую силами поля при малом перемещении ∆S тела, происходящем вдоль произвольно выбранного направления в пространстве, которое обозначим буквой S. Эта работа равна:

где - проекция силы на направление .

Поскольку в данном случае работа совершается за счет запаса потенциальной энергии ∆ , она равна убыли потенциальной энергии -∆ на отрезке оси ∆S:

∆A = -∆

Из двух последних выражений получаем: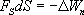

Откуда: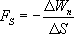

Последнее выражение дает среднее значение на отрезке ∆S. Чтобы получить значение в точке нужно произвести предельный переход:

Так как может изменяться не только при перемещении вдоль оси S, но также и при перемещениях вдоль других направлений, предел в этой формуле представляет собой так называемую частную производную от по S:

Это соотношение справедливо для любого направления в пространстве, в частности и для направлениq декартовых координатных осей х, у, z:

Эта формула определяет проекции вектора силы на координатные оси. Если известны эти проекции, оказывается определенным и сам вектор силы:

в математике вектор , где а - скалярная функция х, у, z, называется градиентом этого скаляра обозначается символом . Следовательно сила равна градиенту потенциальной энергии, взятого с обратным знаком:

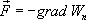
Пусть положительный заряд q перемещается силой электрического поля с эквипотенциальной поверхности, имеющей потенциал, на близко расположенную эквипотенциальную поверхность, имеющую потенциал

Напряженность поля Е на всем малом пути dx можно считать постоянной. Тогда работа перемещения С другой стороны . Из этих уравнений получаем

Знак минус обусловлен тем, что напряженность поля направлена в сторону убывания потенциала, тогда как градиент потенциала направлен в сторону возрастания потенциала.

6. Поток вектора напряжённости электростатического поля. Теорема Гаусса.

Число линий вектора E, пронизывающих некоторую поверхность S, называется потоком вектора напряженности NE.

Для вычисления потока вектора E необходимо разбить площадь S на элементарные площадки dS, в пределах которых поле будет однородным.

Поток напряженности через такую элементарную площадку будет равен по определению.

где - угол между силовой линией и нормалью 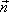к площадке dS; - проекция площадки dS на плоскость, перпендикулярную силовым линиям. Тогда поток напряженности поля через всю поверхность площадки S будет равен

Так как , то:

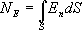
где - проекция вектора на нормаль и к поверхности dS.

Теорема Гаусса утверждает:

Поток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε₀.

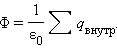
Внешний заряд не создаёт поток.

7. Вычисление напряжённости поля вблизи бесконечной плоскости, нити с поверхностной плотностью заряда σ и линейной плотностью заряда τ.

Расчёт напряжённости бесконечной плоскости

Рассмотрим поле, создаваемое бесконечной однородной заряженной плоскостью. Пусть поверхностная плотность заряда плоскости одинакова и равна σ. Представим себе мысленно цилиндр с образующими, перпендикулярными к плоскости, и основанием ΔS, расположенным относительно плоскости симметрично. В силу симметрии E' = E'' = E. Поток вектора напряжённости равен 2EΔS. Применив теорему Гаусса, получим:

из которого

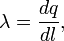
Расчёт напряжённости бесконечной нити

Рассмотрим поле, создаваемое бесконечной нитью с линейной плотностью заряда, равной λ. Пусть требуется определить напряжённость, создаваемую этим полем на расстоянии R от нити. Возьмём в качестве гауссовой поверхности цилиндр с осью, совпадающей с нитью, радиусом R и высотой Δl. Тогда поток напряжённости через эту поверхность рассчитывается следующим образом:

В силу симметрии, модуль напряжённости в любой точке поверхности цилиндра будет одинаков. Тогда поток напряжённости через эту поверхность рассчитывается следующим образом:

Учитывается только площадь боковой поверхности цилиндра, так как поток через основания цилиндра равен нулю. Приравнивая 1 и 2 выражения, получим:

8. Вычисление напряжённости поля вблизи заряженных сферы и шара.

Расчет напряженностей для заряженной сферы (поле заряженной сферы).

Пусть имеется:

а) Полая сфера или шар из проводящего материала. В обоих случаях заряд распределяется по поверхности по закону Кулона. Тогда по теореме О.-Г.

.

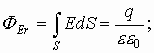
Приравняем интегралы

Аналогичным способом рассуждая, полный поток вектора через сферу любого радиуса r определится как:

Окончательно получаем напряженность в любой точке пространства, расположенной вдали от заряженной полой сферы:

б) Если

Каждый отдельно взятый заряд на поверхности сферы дает силовую линию, которая пересекает сферу радиуса r дважды (со знаком “+” и со знаком “-”, т.е. входящий и выходящий), таким образом результирующее количество векторов Е, пересекающих эту сферу, равно нулю. То есть электрическое поле внутри полой сферы отсутствует.

в) Поле сферы с зарядом, равномерно распределенным по объему.

По закону Кулона (взаимное отталкивание зарядов) в однородном проводящем теле заряды распределяются по поверхности. Поэтому возьмем искусственный случай смеси проводящих элементов в непроводящей массе.

Рассмотрим случай (r > R): Аналогично рассуждая, поток вектора Е через сферу радиуса r определится как:

;
И вновь получим:

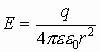- напряженность вдали от сплошной заряженной сферы.

Рассмотрим случай (r < R):

По теореме Гаусса поток вектора Е состоит из двух потоков , где - поток векторов, обусловленный внешним кольцом зарядов относительно сферы радиуса , по определению он  0 (см. пр. тему).

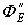- поток векторов Е внутренних зарядов относительно сферы радиуса r:

,
где - заряд внутри сферы r.

Вводится понятие объемной плотности заряда , т.е. количество заряда в единице объёма, тогда количество заряда внутри сферы r определится как:

,
где  - объемная плотность заряда.

По определению:

а также

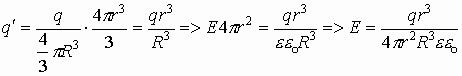
Окончательно получаем, что величина напряженности в любой точке пространства внутри однородно заряженной сферы:

.

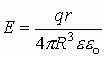Date: 2015-11-13; view: 923; Нарушение авторских прав