Извлечение корней

Извлечение корня есть действие, обратное возведению в степень. Поэтому (см. предыдущий параграф) модуль корня (целой степени) из комплексного числа получается извлечением корня той же степени из модуля подкоренного числа, а аргумент – делением аргумента на показатель корня:

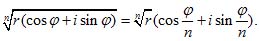
Здесь под знаком обозначено положительное число (арифметический корень из модуля).
Корень n-й степени из всякого комплексного числа имеет n различных значений. Все они Все они имеют одинаковые модули ; аргументы же получаются из аргумента одного из них последовательным прибавлением угла (1/n)*360°.
Действительно, пусть φ0 есть аргумент подкоренного числа. Тогда φ0 + 360°; φ0+2•360° и т. д. также являются его аргументами. Формула (В) показывает, что за аргумент корня можно принять не только 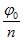, но также 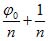360°, 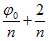360° и т. д. Соответствующие значения корня не все различны между собой: аргумент 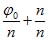360, т. е. 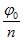+360°, дает то же комплексное число, что и аргумент 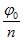; аргумент 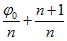360° = 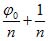360°+360° дает то же комплексное число, что и аргумент 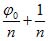360°, и т.д. Различных значений корня будет ровно n. См. примеры.
Пример 1. Извлечь квадратный корень из числа – 9i. Модуль этого числа есть 9. Значит, модуль корня равен 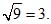Аргумент подкоренного числа можно принять равным - 90°, - 90°+360°, - 90°+2•360° и т. д.
В первом случае получаем:

(1)

Во втором случае

(2)

В третьем случае

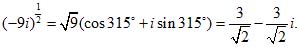
т. e. то же, что в первом. Беря φ = - 90° + 3 • 360°, - 90° + 4 • 360° или φ = - 90° - 360°; - 90° - 2•360° и т. д., мы будем поочередно получать значения (1) и (2). Пример 2. Извлечь квадратный корень из числа 16. Аргумент этого числа есть 360°k (k – целое число). Аргумент корня будет 360 k: 2 = 180k. Если k есть нуль или четное число, то аргумент корня равен нулю или кратен 360°. Тогда 16^1/2= 4 (cos 0° +isin 0°) = 4. Если же k – нечетное число, то аргумент будет 180° или отличаться от 180° на кратное 360°. Тогда 16^1/2 = 4 (соs 180° + isin180°) = - 4.
Пример 3. Извлечь кубический корень из 1. Модуль корня равен 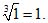Аргумент подкоренного числа есть 360k (k –любое целое число). Аргумент корня будет 120°k. Полагая k = 0,1,2, находим три значения аргумента корня: 0°, 120°, 240°. Соответствующие значения корня будут*:
z1 = cos 0° + isin 0° = 1,
z2 = cos 120° + isin 120° =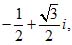
z3 = cos 240° + isin 240° =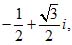
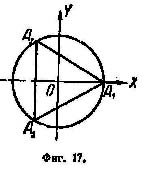На фиг. 17 эти значения изображены точками A1, A2, A3.
Треугольник A1A2A3 – равносторонний. Он вписан в окружность радиуса 1.
Пример 4. Извлечь корень шестой степени из -1. Аргумент подкоренного числа -1 есть 180° + 360°k. Аргумент корня равен 30° + 60°k. Имеем следующие шесть значений корня:
z1 = cos 30° + isin 30° =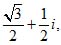
z2 = cos 90° + isin 90° = i,
z3 = cos 150° + isin 150° = _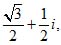
z4 = cos 210° + isin 210° = _
z5 = cos 270° + isin 270° = - i,
z6 = cos 330° + isin 330° = _
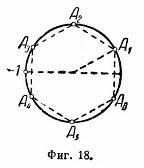
Точки A1, A2, A3, A4, A5, A6, изображающие эти значения (фиг. 18), являются вершинами правильного шестиугольника.

Из формулы (В) следует, что n корней из какого-либо комплексного числа и n корней из сопряженного числа попарно сопряжены.
Пример 5. Корни четвертой степени из числа 16(cos120° + isin120°) = - 8 + 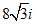будут:
z1 = 2(cos 30° + isin 30°) = 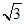+ i;
z2 = 2(cos 120° + isin 120°) = -1 + 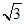i;
z3 = 2(cos 210° + isin 210°) = _ 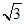- i;
z4 = 2(cos 300° + isin 300°) = 1 - 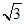i,
а корни той же степени из числа 16 (cos120° - isin120°) = -8 - 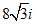будут:
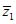= 2(cos 30° - isin 30°) = 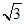- i;
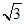= 2(cos 120° - isin 120°) = -1 - i;
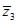= 2(cos 210° - isin 210°) = - 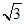+ i;
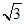= 2(cos 300° - isin 300°) = 1 + i.
Числа z1 и 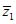, z2 и и т. д. попарно сопряжены.

Date: 2015-12-11; view: 316; Нарушение авторских прав