
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Дмух Галина Юрьевна
|
|
КОМПЛЕКСНЫЕ ЧИСЛА В ЭЛЕКТРОТЕХНИКЕ
КОМПЛЕКСНЫЕ ЧИСЛА В ЭЛЕКТРОТЕХНИКЕ
Мангушев Виталий Иванович
студент 2 курса, факультет электроэнергетики и электротехники ДВФУ, г. Владивосток
E-mail: vitalya-53@mail.ru
Дмух Галина Юрьевна
научный руководитель, канд. пед. наук, доцент кафедры алгебры, геометрии и анализа ДВФУ, г. Владивосток
В математике очень широко применяется решение задач с помощью комплексных чисел, но что такое комплексные числа и как они нашли себя в электротехнике?
Первоначально математики столкнулись с мнимой единицей i=  , когда стало не хватать действительного числа, а именно при решении простейшего квадратного уравнения
, когда стало не хватать действительного числа, а именно при решении простейшего квадратного уравнения 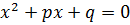 , где «p» и «q» — действительные числа. При вычислении его корней по всем известным формулам, математики еще до XVI века сталкивались с проблемой отрицательного корня. В действительности, никто не мог объяснить какой смысл следует придавать этому выражению и, в следствие, решили, что корень из отрицательного числа не имеет смысла. И это работало, было легко показать, что при отрицательном корне, решением было ни положительное число, ни отрицательное, ни нуль.
, где «p» и «q» — действительные числа. При вычислении его корней по всем известным формулам, математики еще до XVI века сталкивались с проблемой отрицательного корня. В действительности, никто не мог объяснить какой смысл следует придавать этому выражению и, в следствие, решили, что корень из отрицательного числа не имеет смысла. И это работало, было легко показать, что при отрицательном корне, решением было ни положительное число, ни отрицательное, ни нуль.
Однако в дальнейшем, при решении кубических уравнений отказываться от отрицательного корня уже было невозможно. В 1543 году несколько итальянских ученых выдвинули формулу «Кардано» позволяющую решать уравнения третьей степени вида:
 , а именно:
, а именно:  , где
, где 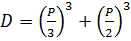 , она вполне рабочая, но при решении уравнений имеющих три различных действительных корня она не дает ожидаемого результата. Например, корнями уравнения
, она вполне рабочая, но при решении уравнений имеющих три различных действительных корня она не дает ожидаемого результата. Например, корнями уравнения  легко доказать, являются числа 0,1,–1, но при решении уравнения методом, изложенным выше, результат удивляет:
легко доказать, являются числа 0,1,–1, но при решении уравнения методом, изложенным выше, результат удивляет:  и как же получить из этого три нужных нам корня?
и как же получить из этого три нужных нам корня?
После этого математики пошли на изучение мнимых чисел, дали возможность им существовать. Затем было обнаружено, что многие громоздкие задачи в математике решаются гораздо проще, если пользоваться мнимыми числами. К.Ф. Гаусс предложил называть мнимые числа комплексными, что впоследствии прижилось.
С похожей проблемой ученые столкнулись при решении задач электротехники.
Описание электромагнитных процессов в цепях переменного тока сводится к решению множества интегралов, а решение их становится столь сложным, что взять их не пол силу даже опытным математикам. Определение крайне упростилось и стало более элегантно при применении комплексных чисел.
Из физики мы знаем, что переменным током называется ток, изменяющийся во времени. Из всех возможных форм периодических токов наибольшее распространение имеет синусоидальный ток, так как у него есть преимущество в плане экономии энергоресурсов.
Любая синусоидальная функция времени «a(t)» может быть однозначно задана тремя параметрами: амплитудой, частотой и начальной фазой. Ее формула для любого момента времени «t»: 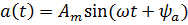 , где
, где  — максимальное значение функции или её амплитуда;
— максимальное значение функции или её амплитуда;  – угловая частота,
– угловая частота,  начальная фаза (угол функции в момент времени принятый за начало отсчета, т. е. при
начальная фаза (угол функции в момент времени принятый за начало отсчета, т. е. при  ), аргумент
), аргумент  называется фаза или фазовый угол, он определяет значение функции
называется фаза или фазовый угол, он определяет значение функции  в любой момент времени. В электрических цепях переменного тока синусоидальными функциями времени являются ток, падение напряжения и ЭДС:
в любой момент времени. В электрических цепях переменного тока синусоидальными функциями времени являются ток, падение напряжения и ЭДС:

В электротехнике принято обозначать мгновенные значения токов строчными буквами в виде:  ; А амплитуду заглавной с нижним индексом «
; А амплитуду заглавной с нижним индексом «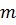 »:
»:  .
.
Так же существует действующий(эффективный) ток. По закону Джоуля-Ленца на участке тока сопротивлением «r», за время «T», соответствующее периоду тока «i», будет выделено количество тепла равное: 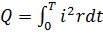 , с другой стороны при постоянном токе на этом же участке выделится равное количество энергии:
, с другой стороны при постоянном токе на этом же участке выделится равное количество энергии:  , если приравнять данные формулы, можно вывести действующее значение тока
, если приравнять данные формулы, можно вывести действующее значение тока  .
.

Отсюда — действующий ток это среднеквадратичное значение переменного тока. По аналогии можно рассчитать действующее значение напряжения и ЭДС, которые так же равняются среднеквадратичной своей соответствующей.

Рисунок 1. Представление синусоиды тока в виде вращающегося вектора
Из курса математики известно, что синусоидальная функция времени может быть представлена в виде вращающегося вектора длиной  с угловой частотой
с угловой частотой  . Положение этого вектора в начальный момент времени t = 0 должно составлять угол
. Положение этого вектора в начальный момент времени t = 0 должно составлять угол  с осью абсцисс.
с осью абсцисс.
Наиболее удобная для проведения расчетов координатная система стала комплексная, так как вектор можно определить четырьмя различными формами записи:
· Алгебраическая форма:  , надо заметить, что в математике знак мнимой части используется как «
, надо заметить, что в математике знак мнимой части используется как «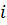 », но в электротехнике этим знаком обозначается ток, по этому было решено заменить его на «
», но в электротехнике этим знаком обозначается ток, по этому было решено заменить его на « ». Знак «
». Знак « » не говорит ни о каком-либо сложении, он только указывает на то, что мы объединяем два действительных числа в нечто единое. На комплексной плоскости «
» не говорит ни о каком-либо сложении, он только указывает на то, что мы объединяем два действительных числа в нечто единое. На комплексной плоскости « » и «
» и « » координаты конца вектора тока, по мнимой и действительной оси.
» координаты конца вектора тока, по мнимой и действительной оси.
· Тригонометрическая форма:  запись результата вещественной и мнимой части через модуль «
запись результата вещественной и мнимой части через модуль « » и аргумент «
» и аргумент « »
»
· Показательная форма:  — получается путем применения формулы Эйлера к тригонометрической.
— получается путем применения формулы Эйлера к тригонометрической.
· Полярная форма:  — запись, не использующаяся для расчетов.
— запись, не использующаяся для расчетов.
Рассмотрим типичную задачу в электротехнике: сложение токов.
Включим в цепь переменного тока две параллельные ветви, содержащие некое сопротивление. Нам известны: амплитуда, частота и начальная фаза токов, равная нулю.  ,
, 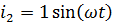

Рисунок 2. Токи в параллельных ветвях цепи переменного тока
По одному из главных постулатов электротехники, а именно по I-му закону Кирхгофа (Алгебраическая сумма токов в узле равна нулю  )
)  , отсюда
, отсюда  , графически это можно определить так:
, графически это можно определить так:

Рисунок 3. Сложение синусоид тока
Как видно, это было легко, при фазе равной нулю решение такой задачи обуславливается сложением значения амплитуд в каждый момент времени.  . Всё просто.
. Всё просто.
А теперь представим, что фаза у токов отличается. Например,  равняется не нулю, а скажем, 30
равняется не нулю, а скажем, 30  , попробуем проделать задачу тем же способом:
, попробуем проделать задачу тем же способом:

Рисунок 4. Синусоиды тока с разной фазой
Решение:
 ;
;
по формуле суммы углов:



Воспользуемся методом введения дополнительного угла, чтобы привести уравнение к виду:  ;
;
Так как у нас есть составляющие:  и
и 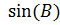 , найдем
, найдем  и
и  .
.
По основному тождеству тригонометрии:  , значит:
, значит:

Находим  и
и  через
через  и
и  :
:
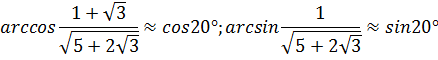
Подставляем в 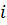 :
:

 .
.
Как видим, такая, простая на первый взгляд, задача переливается в уравнение, которое заставит посидеть и подумать «как же оно решается?», а ведь это самое наипростейшее усложнение.
Теперь рассмотрим эту задачу с применением комплексных чисел, мы уже знаем, что такое комплексное число и в состоянии перевести в него уравнение синусоиды тока.
Итак:
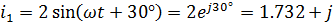 ;
;  ,
,
сложим:
 .
.
Решение в 2 строки, а результаты те же.
Проверим это на векторной диаграмме:

Рисунок 5. Векторная диаграмма
Выводы: На этом простейшем примере хорошо видно как комплексные числа упростили решение. Сейчас же ни одна задача в электротехнике не решается без них. Мнимые числа необходимая составляющая электротехники.
Список литературы:
1.Балк М.Б., Балк Г.Д., Полухин А.А. «Реальные применения мнимых чисел» // изд. «Радянська школа», 1988 г — 5—16 с.
2.Голубев А.Н. Доктор техн. наук, профессор, «Лекция по ТОЭ № 3 — Представление синусоидальных величин с помощью векторов и комплексных чисел».
3.Ландсберг Г.С. Элементарный учебник физики, том 2. «Электричество и магнетизм», § 160 «Сложение токов при параллельном включении сопротивлений в цепь переменного тока» — 384—389 с.
4.Мацкевич И.Ю. «Высшая математика приложения в физике и электронике» учебно-методическое пособие// МГВРК Минск 2008 — 5—7 с.
| <== предыдущая | | | следующая ==> |
| | | Виды проницаемости и методы ее определения |
Date: 2015-12-11; view: 1091; Нарушение авторских прав