Арифметические операции над ними

Введение

Методические указания предназначены студентам младших курсов всех специальностей бакалаврской подготовки в качестве руководства к выполнению типовой расчетной работы по теме: «Вычисление пределов функций одной переменной».

Основная цель работы – привитие студентам практических навыков в решении задач по указанной теме, связанных исключительно с техникой вычисления пределов. Поэтому в ней приводится систематическое изложение необходимого теоретического материала. Предполагается, что пользующиеся этим указаниями прослушали курс лекций по математическому анализу за первый семестр в объеме, определяемом действующими учебными планами по соответствующим специальностям УГАТУ.

Студентам, ощущающим потребность в расширении и, главное, более прочном обосновании своих знаний по курсу математического анализа, мы рекомендуем следующую литературу:

1. Кудрявцев Л.Д. Математический анализ, т.1. – М.: Высшая школа, 1973 г.

2. Пискунов Н.С. Дифференциальное и интегральное исчисления, т.1.-М.: Наука, 1972 г.

3. Смирнов В.И. Курс высшей математики, т.1. – М.: Наука, 1967 г.

4. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т.1. – М.: Наука, 1968 г.

Пределы элементарных функций

Арифметические операции над ними

Класс элементарных функций состоит из простейших элементарных функций и из всех тех функций, которые выражаются через них в конечном виде, т.е. с помощью числа арифметических действий и суперпозиций.

Если является элементарной функцией, то вычисление , когда предельное значение аргумента принадлежит области определения , сводится к простой подстановке значения вместо , т.е.

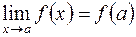(1)

Пример 1. Вычислить .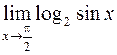

Решение. Данная функция является элементарной, она представляется как суперпозиция функций . Предельное значение 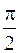принадлежит области определения, поэтому

.

Пример 2. Вычислить .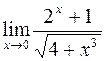

Решение. Нетрудно проверить, что функция равенство (1) выполняется, поэтому

При вычислении пределов наибольший интерес представляют случаи, когда по тем или иным причинам условие (1) будет нарушено. Это может привести к некоторым дополнительным сложностям. Преодолеть эти сложности иногда удается с помощью тождественных преобразований самой функции, иногда путем использования основных теорем о пределах и т.д. В более сложных примерах нахождение пределов потребует применения специальных технических приемов, рассмотрением которых мы и займемся ниже. А пока – несколько более простых примеров.

Пример 3. Вычислить .

Решение. Значение аргумента не принадлежит области определения функции; условие (1) нарушено. Преобразуем функцию, разложив числитель и знаменатель на множители:

.

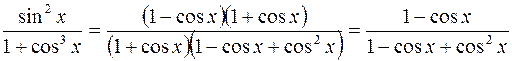Тогда по теореме о пределе частного двух функций, получим

.

Пример 4. .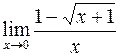

Решение. В данном примере так же условие (1) нарушено. Преобразования таковы:

.

тогда

.

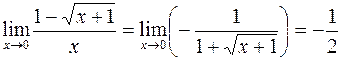Пример 5. .

Пример 6. Вычислить .

Решение. Здесь мы имеем предел показательно-степенного выражения, т.е. выражения вида 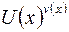. Можно использовать преобразование

.

Если же функции и 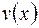имеют конечные пределы, то еще проще:

.

В нашем примере .

Так как , то . Искомый предел равен 0.

Date: 2015-12-10; view: 405; Нарушение авторских прав