Расчеты стержневых систем на устойчивость

При расчетах конструкций на устойчивость используем уравнение (5.3), в котором матрица жесткости определяется так же, как при статическом расчете, а матрица геометрической жесткости вычисляется методом сложения жесткостей отдельных элементов.

Матрица геометрической жесткости для отдельного элемента (Рис.5.6)

,

где (5.10)

- компонент матрицы геометрической жесткости сжатого конечного элемента. Функции определены формулами (5.5).

Вычисляя по (5.10), (5.5) при , получаем

. (5.11)

геометрическую матрицу жесткости стержневого элемента.

Рассмотрим стойки с различными закреплениями концов (Рис. 5.7).

На Рис.5.7a изображена стойка со свободным верхним концом. На рис.5.8 показана расчетная схема этой стойки, принятая в виде одного конечного элемента с двумя неизвестными перемещениями свободного конца: Z₁ и Z₂.

Матрица жесткости для стойки вычисляется с помощью (5.7):

.

Матрица геометрической жесткости вычисляется по (5.11):

.

После подстановки найденных значений в (5.3) получаем

. (5.12)

После простых преобразований (5.12) приводится к виду

.

В том случае, когда 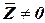, необходимо чтобы детерминант матрицы, стоящей в скобках, был равен нулю. Это приводит к решению уравнения:

,

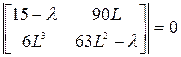где 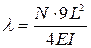, (5.13)

или, раскрывая определитель, получаем квадратное уравнение:

,

корни которого равны

, .

Из (5.13) находим наименьшую критическую силу

.

Точное значение критической силы для этой стойки

.

Погрешность МКЭ составила 0.81%.

На рис.5.7б изображена стойка с плавающей заделкой на верхнем конце. На рис.5.9 показана расчетная схема этой стойки, принятая в виде одного конечного элемента с одним неизвестным поступательным перемещением конца: Z₁.

Матрица жесткости и матрица геометрической жесткости для неё вычисляется с помощью (5.7), (5.11):

,

После подстановки найденных значений в (5.3) получаем

.

При , ,

откуда .

Точное значение критической силы для этой стойки

.

Погрешность МКЭ составила 1.3%.

На рис.5.7в изображена стойка со связями, препятствующими перемещениям и повороту концевых сечений.

На рис.5.10 показана расчетная схема этой стойки, принятая в виде двух конечных элементов с одним неизвестным поступательным перемещением середины стойки: Z₁.

Матрица жесткости и матрица геометрической жесткости для неё вычисляется с помощью выражений(5.7), (5.11)

,

.

После подстановки найденных значений в (5.3) получаем

,

откуда находим при , . Точное значение критической силы для этой стойки

.

Погрешность МКЭ составила 1.3%.

На рис.5.7г изображена стойка с жестко заделанным и шарнирно опертым концами.

На рис.5.11 показана расчетная схема этой стойки, принятая в виде двух конечных элементов с тремя неизвестными: поступательным перемещением середины стойки Z₁, углом поворота среднего сечения Z₂ и углом поворота шарнирно опертого сечения Z₃.

С помощью (5.7) вычисляются элементы матрицы жесткости:

, ,

,

,

,

.

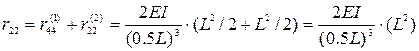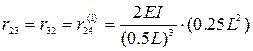и с помощью (5.11) вычисляются элементы матрицы геометрической жесткости:

, ,

,

,

,

.

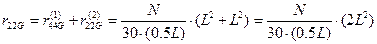После подстановки найденных значений в (5.3) получаем

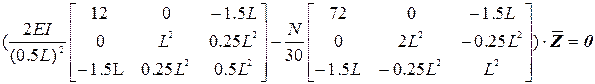
при , получим уравнение

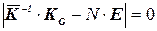, (5.14)

где .

Раскрыв определитель (5.14), получим алгебраическое уравнение третьего порядка, решив которое найдем корни N_i. Наименьший корень даст величину критической силы для стойки.

Расчет проведем, используя программный пакет Maple:

> restart;

> EI:=EI:L:=6.:

> with(LinearAlgebra):

> K:=2.*EI/((0.5*L)^2)*<<L^2/2|-1.5*L|L^2/4>,<-1.5*L|12|0>,<L^2/4|0|L^2>>;

> KG:=1/30*<<L^2|-1.5*L|-L^2/4>,<-1.5*L|72|0>,<-L^2/4|0|2*L^2>>;

> Sob_chisla:=Eigenvalues(K^(-1).KG);

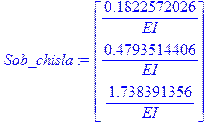
Наибольшее собственное число матрицы : 1.738391356/EI равно обратному значению критической силы для этой стойки:

Точное значение критической силы для этой стойки

.

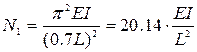Погрешность МКЭ составила 0.191%.

На рис.5.7д изображена шарнирно опертая стойка. На рис.5.12 показана расчетная схема этой стойки, принятая в виде двух конечных элементов с четырьмя неизвестными: углами поворотов шарнирно опертых сечений Z₁ и Z₄ , поступательным перемещением середины стойки Z₁ и углом поворота среднего сечения Z₂.

С помощью (5.7) вычисляются элементы матрицы жесткости:

, , , , ,

, ,

, ,

, , , , , , .

и с помощью (5.11) вычисляются элементы матрицы геометрической жесткости:

, , , , ,

, ,

, ,

, , , , , , .

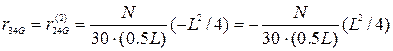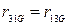После подстановки найденных значений в (5.3) получаем

,

при , получим уравнение

, (5.14)

где .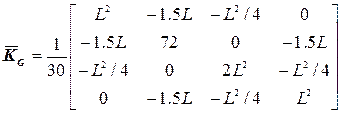

Раскрыв определитель (5.14) получим алгебраическое уравнение четвертого порядка, решив которое найдем корни N_i. Наименьший корень даст величину критической силы для стойки.

Расчет проведем, используя программный пакет Maple:

> restart;

> EI:=EI:L:=6.:

> with(LinearAlgebra):

> K:=2.*EI/((0.5*L)^2)*<<L^2/2|-1.5*L|L^2/4|0>,<-1.5*L|12|0|1.5*L>,<L^2/4|0|L^2|L^2/4>,<0|1.5*L|L^2/4|L^2/2>>;

> KG:=1/30*<<L^2|-1.5*L|-L^2/4|0>,<-1.5*L|72|0|1.5*L>,<-L^2/4|0|2*L^2|-L^2/4>,<0|1.5*L|-L^2/4|L^2>>;

> Sob_chisla:=Eigenvalues(K^(-1).KG);

Наибольшее собственное число матрицы : 3.620329309/EI равно обратному значению критической силы для этой стойки:

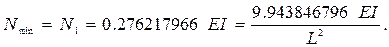
Точное значение критической силы для этой стойки

.

Погрешность МКЭ составила 0.752%.

Мы провели расчеты всех вариантов стоек постоянной жесткости с различными закреплениями концов по МКЭ. Для стоек с одним подвижным концом стойка рассматривалась состоящей из одного конечного элемента, а для стоек с неподвижными концами – состоящей из двух конечных элементов. Сравнив результаты расчетов с точными решениями видим, что погрешность МКЭ для всех случаев меньше 1.5 %.

Определим критический параметр N для одноэтажной рамы, показанной на рис.5.13. Рама имеет два жестких смещающихся в горизонтальном направлении узла. Расчетная схема принята в виде трех конечных элементов (смотри рис.5.14): левая стойка, ригель и правая стойка. Неизвестными считаем: горизонтальное перемещение ригеля Z₁, угол поворота левого Z₂ и угол поворота правого узла Z₃.

С помощью (5.7) вычисляются элементы матрицы жесткости:

, , ,

,

, ,

, , .

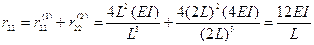и с помощью (5.11) вычисляются элементы матрицы геометрической жесткости:

После подстановки найденных значений в (5.3) получаем

,

при , получим уравнение

, (5.15)

где . (5.16)

Раскрыв определитель (5.15) получим алгебраическое уравнение третьего порядка, решив которое найдем корни N_i. Наименьший корень даст величину критического параметра для рамы на рис.5.13. Или можно найти собственные числа: , для матрицы . Наибольшее собственное число даст величину обратную критическому параметру.

Расчет проведем, используя программный пакет Maple:

Date: 2015-12-10; view: 1023; Нарушение авторских прав