
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Динамический расчет систем со многими степенями свободы
|
|
4.1.1. Произвольная нагрузка
Решение задач динамики стержневых систем с конечным числом степеней свободы сводится к решению матричного уравнения:
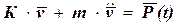 , (4.1)
, (4.1)
в котором К – матрица жесткости системы, m – матрица масс,
Решение уравнения (4.1) будем искать в виде разложения:
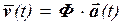 , (4.2)
, (4.2)
где 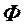 – некоторая квадратная матрица,
– некоторая квадратная матрица, 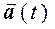 - вектор коэффициентов, зависящих от времени.
- вектор коэффициентов, зависящих от времени.
После подстановки (4.2) в (4.1), умножения на  слева получаем
слева получаем
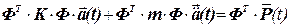 (4.3)
(4.3)
Обозначим
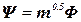 (4.4)
(4.4)
получим

Обозначим 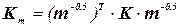 , тогда
, тогда
 . (4.5)
. (4.5)
В качестве матрицы 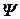 выберем матрицу нормированных собственных векторов матрицы Km. Тогда
выберем матрицу нормированных собственных векторов матрицы Km. Тогда
 (4.6)
(4.6)  - матрица собственных значений матрицы Km,
- матрица собственных значений матрицы Km,
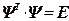 , (4.7) Е – единичная матрица.
, (4.7) Е – единичная матрица.
После подстановки (4.6) и (4.7) в (4.5) получаем векторное равенство:
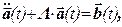 (4.8)
(4.8)  . (4.9)
. (4.9)
Из обыкновенных неоднородных дифференциальных уравнений (4.8) находим коэффициенты 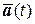 и согласно (4.2) решение поставленной задачи:
и согласно (4.2) решение поставленной задачи:
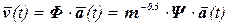 . (4.10)
. (4.10)
Уравнение (4.8) представляет собой систему независимых линейных дифференциальных уравнений второго порядка:
 (4.11)
(4.11)
где  - собственная частота i –й формы колебаний. Для получения решения уравнения (4.11) при действии на систему произвольной нагрузки
- собственная частота i –й формы колебаний. Для получения решения уравнения (4.11) при действии на систему произвольной нагрузки 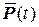 достаточно знать импульсную переходную функцию (ИПФ), которая представляет собой решение этого уравнения при
достаточно знать импульсную переходную функцию (ИПФ), которая представляет собой решение этого уравнения при 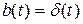 ,
,  – дельта-функция Дирака.
– дельта-функция Дирака.
 (4.12)
(4.12)
Решение уравнения (4.12) хорошо известно:
 , (4.13)
, (4.13)
тогда решение (4.11) при любом b(t), действующем при t > 0, имеет вид
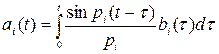 ,
,
или с учетом (4.9)

и в матричной форме
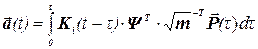 .
.
Примем 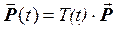 , тогда, обозначив
, тогда, обозначив
 , (4.14)
, (4.14)
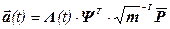 . (4.15)
. (4.15)
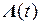 - диагональная матрица, элементами которой являются функции (4.14).
- диагональная матрица, элементами которой являются функции (4.14).
Из (4.10) определяем динамические перемещения
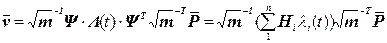 , (4.16)
, (4.16)
где 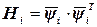 - (4.17)
- (4.17)
парциальная матрица.
Формулы, полученные в этом разделе, относятся к случаю отсутствия диссипативных сил. В таких системах после исчезновения возмущающих нагрузок механическая энергия остается постоянной, вследствие чего колебания с течением времени не затухают.
Для учета диссипативных сил в уравнение движения (4.1) необходимо ввести дополнительное слагаемое, учитывающее силы неупругого сопротивления движению. Из-за многообразия сил сопротивления (внешнего трения сухого и вязкого, внутреннего трения в материале и т.п.), и представления их различными моделями неупругого сопротивления (линейными и нелинейными, зависящими и независящими от частоты или амплитуды и т.д.) колебаний, невозможно однозначно ввести диссипативное слагаемое в (4.1).
В настоящее время нормативными документами рекомендуется использовать физически реализуемые модели сопротивления. К этим моделям относятся: скорректированная модель Фохта (вязкого трения) и частотно-независимая модель внутреннего трения.
Эти модели допускают разложение линейных операторов диссипативных сил по формам операторов упругих сил, в результате поиска решения (4.1) в виде такого разложения (4.10) приходим к решению системы независимых линейных уравнений относительно коэффициентов a(t).
Для решения динамической задачи при любом воздействии на систему достаточно получить импульсную переходную функцию для уравнения типа (4.11).
Не приводя выкладок для разных моделей внутреннего сопротивления, запишем результат, используемый в инженерной практике:
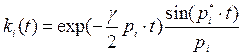 . (4.18)
. (4.18)
Решение задачи представлено формулой (4.16), в которой вместо (4.13) используется импульсная переходная функция (4.18).
4.1.2. Гармоническая нагрузка
Рассмотрим колебания системы при действии на неё гармонической нагрузки: 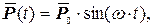
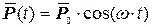 или
или 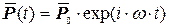 . Функция нагрузки
. Функция нагрузки  ,
, 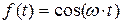 или
или  . Используя формулы Эйлера:
. Используя формулы Эйлера:
 ,
, 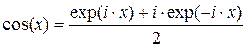 ,
,
достаточно рассмотреть случай 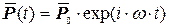 .
.
Для диссипативной системы уравнение движения системы с моделью внутреннего трения по скорректированному Фохту имеет вид:
 , (4.19)
, (4.19)
где 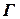 - диссипативная матрица.
- диссипативная матрица.
Подставив в (4.19)  ,
, 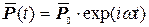 , после сокращения на
, после сокращения на 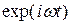 , получим:
, получим:
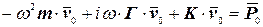 . (4.20)
. (4.20)
Решение уравнения (4.20) ищем в виде разложения по собственным формам  матриц
матриц  , m:
, m:
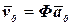 . (4.21)
. (4.21)
После подстановки (4.21) в (4.20), умножения полученного на  слева, с учетом выражений, определяющих собственные значения и собственные векторы:
слева, с учетом выражений, определяющих собственные значения и собственные векторы:
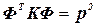 ,
,  ,
, 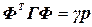 (4.22)
(4.22)
получаем 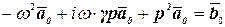 , (4.23)
, (4.23)
где 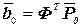 . (4.24)
. (4.24)
Система дифференциальных уравнений (4.23) в силу диагональности матриц 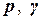 , представляет собой систему независимых уравнений:
, представляет собой систему независимых уравнений:
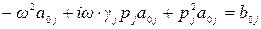 ,
,
из которых находим 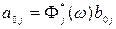 ,
,
где 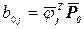 ,
,  , (4.25)
, (4.25)
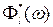 - передаточная функция,
- передаточная функция,  - амплитудно-частотные характеристики (АЧХ),
- амплитудно-частотные характеристики (АЧХ),  - фазово-частотные характеристики (ФЧХ) для j -й формы:
- фазово-частотные характеристики (ФЧХ) для j -й формы: 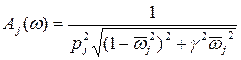 ,
, 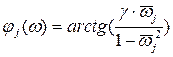 ,
,  . (4.26)
. (4.26)
После подстановки в (4.21) найденных выражений получим
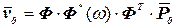 ,
,
или  , (4.27)
, (4.27)
где  (4.28)
(4.28)
- гармоническая матрица податливости,
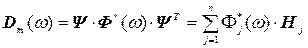 , (4.29)
, (4.29)
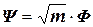 ,
, 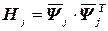 - парциальная матрица,
- парциальная матрица,  - передаточные функции.
- передаточные функции.
Для консервативных систем передаточные функции величины действительные, поэтому амплитуды 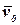 (4.27) величины действительные. Для диссипативных систем передаточные функции (4.25) величины комплексные и
(4.27) величины действительные. Для диссипативных систем передаточные функции (4.25) величины комплексные и  - величина комплексная,
- величина комплексная,  - действительная часть
- действительная часть  ,
, 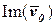 - мнимая часть
- мнимая часть  . Действительную амплитуду находим по формуле:
. Действительную амплитуду находим по формуле:  .
.
Для систем с редким спектром частот упростим вычисление амплитуд колебаний. При  амплитудно-частотная характеристика (АЧХ)
амплитудно-частотная характеристика (АЧХ)  ,
,  ,
, 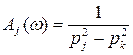 ,
, 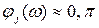 ; т.е. при
; т.е. при 
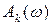 >>
>>  ,
,  . (4.30)
. (4.30)
Такие значения амплитуд принимаем для любых резонансных зон 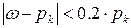 .
.
При других значениях 
 . (4.31)
. (4.31)
Date: 2015-12-10; view: 635; Нарушение авторских прав