Собственные числа и собственные векторы матриц

(1.1)

Если для квадратной матрицы A можно найти вектор и число , от­вечающие выражению (1.1), то этот вектор и это число называются собственным значением и собственным вектором матрицы A.

Решение (1.1) на первый взгляд несложно. В частности, из (1.1) сле­дует система линейных уравнений, коэффициенты которых выража­ются через элементы матрицы A и собственные числа :

(1.2)

Система однородных линейных уравнений (1.2) имеет ненулевое ре­шение в том случае, если определитель матрицы коэффициентов равен нулю:

. (1.3)

Для матрицы A – порядка n уравнение (1.3) есть алгебраическое урав­нение степени n, решив которое можно найти n собственных чисел , i=1,2,…..n, после их подстановки в (1.3) и решения n систем однородных линейных уравнений n – го порядка можно получить n – собственных век­торов.

Пример №6:

Дано:

Найти: собственные числа собственные векторы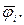

Решение: составим характеристическое уравнение (1.3):

Корни этого уравнения есть собственные числа мат­рицы А: , . Находим собственные векторы, подставив значение в (1.2):

,

откуда , из условия нормирования находим , . Аналогично находим компоненты второго собственного век­тора, после подстановки в (1.2) :

,

откуда , из условия нормирования находим , .

Таким образом, найдены матрицы собственных значений , и собственных векторов .

Из изложенного выше следует, что описанный метод хорош только для матриц невысокого порядка и приводит к существенным вычислитель­ным трудностям при больших n.

Для матриц высокого порядка очень эффективен способ итераций, который состоит в следующем: задаются произвольным вектором , затем используют (1.1), проводя вычисления по схеме:

……… (1.4)

до тех пор, пока в пределах требуемой точности , не совпадут с , .

В (1.4) i это не номер собственного значения, а номер приближения для одного и того же собственного числа. Процесс (1.4) довольно быстро сходится к большему по величине собственному числу и к соответствую­щему ему собственному вектору. Следовательно, методом итераций можно найти только старшее собственное число.

Пример №7:

Дано:

Найти старшее собственное число соответствующий ему собствен­ный вектор.

Решение: зададим нормальный вектор: после чего действуем по (1.4).

После первой итерации находим

92,504053965=

После второй итерации:

.

…………………………………………………………………………………………

После четвертой итерации: , .

Date: 2015-12-10; view: 455; Нарушение авторских прав