
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Проекция точки на плоскость
|
|
· Определите координаты проекции точки М1(-1,-2.5) на плоскость
x-2y+2z-4=0
Нормальный вектор плоскости x-2y+2z-4=0
имеет координаты (1.-2.2), следовательно, вектор является направляющим вектором прямой a. Теперь мы можем написать параметрические уравнения прямой в пространстве, так как знаем координаты точки прямой М1(-1,-2.5) и координаты ее направляющего вектора (1.-):
X=1t-1
Y=-2t-2
Z=2t+5
Осталось определить координаты точки пересечения прямой и плоскости. Для этого в уравнение плоскости  подставим
подставим  :
:
 .
.
Теперь по параметрическим уравнениям  вычислим значения переменных x, y и z при
вычислим значения переменных x, y и z при  :
:
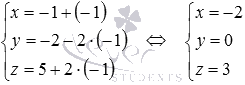 .
.
Таким образом, проекция точки М1 на плоскость АВС имеет координаты 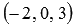 .
.
Проекция прямой на плоскость
Эллипс
Эллипсом называется множество точек плоскости, сумма расстояний которых до двух данных точек, называемых фокусами 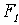 и
и 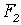 есть величина постоянная (ее обозначают через 2*а). Причем эта постоянная больше расстояния между фокусами.
есть величина постоянная (ее обозначают через 2*а). Причем эта постоянная больше расстояния между фокусами.
Для вывода уравнения эллипса выберем систему координат  так, чтобы фокусы F1 и F2 лежали на оси
так, чтобы фокусы F1 и F2 лежали на оси  , а начало координат совпадало с серединой отрезка F1F2. Тогда фокусы будут иметь следующие координаты:
, а начало координат совпадало с серединой отрезка F1F2. Тогда фокусы будут иметь следующие координаты:  и
и 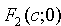 .
.
Пусть  — произвольная точка эллипса. Тогда, согласно определению эллипса,
— произвольная точка эллипса. Тогда, согласно определению эллипса,  , т. е.
, т. е.
 (11.5)
(11.5)
Это, по сути, и есть уравнение эллипса.
Преобразуем уравнение (11.5) к более простому виду следующим образом:
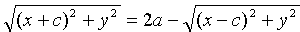 ,
,
 ,
,
 ,
,
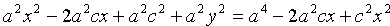 ,
,
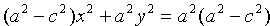 .
.
Так как a > с, то 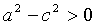 . Положим
. Положим
 (11.6)
(11.6)
Тогда последнее уравнение примет вид 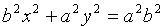 или
или
 (11.7)
(11.7)
Эксцентрисите́т — числовая характеристика конического сечения, показывающая степень его отклонения от окружности. Обычно обозначается “  ” или “
” или “  ”.
”.
Форма эллипса (мера его "сжатия") характеризуется его эксцентриситетом.
 (так как
(так как  , то
, то  )
)
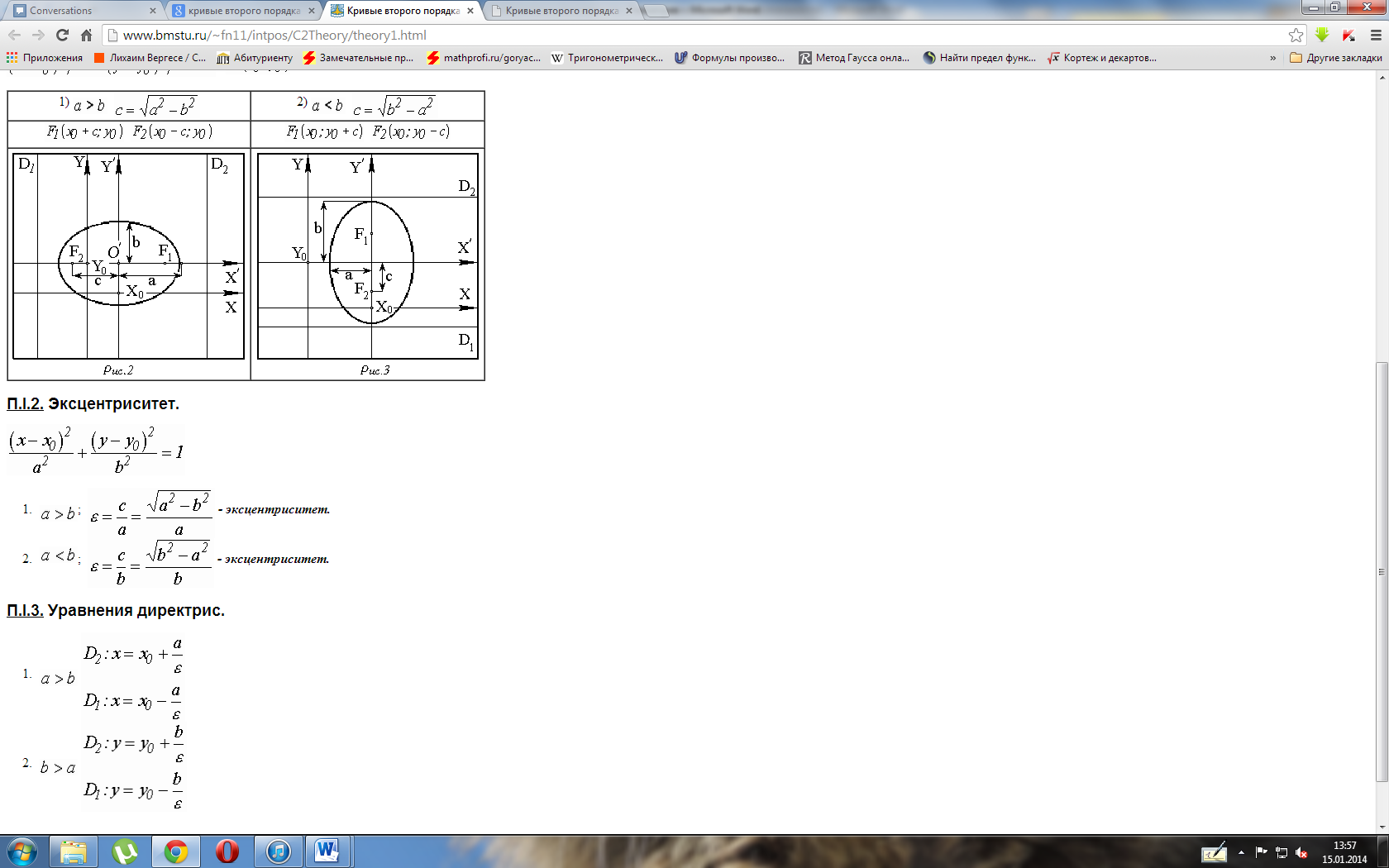 Прямые:
Прямые: 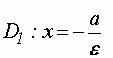 и
и  перпендикулярные главной оси и проходящие на расстоянии
перпендикулярные главной оси и проходящие на расстоянии  от центра, называются директрисами эллипса.
от центра, называются директрисами эллипса.
Параметрические уравнения эллипса
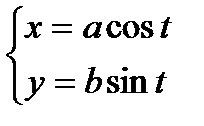


Date: 2015-12-10; view: 432; Нарушение авторских прав