Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Магнитное взаимодействие токов
|
|
Магнитные явления были известны еще в древнем мире. Компас был изобретен более 4500 лет тому назад. В Европе он появился приблизительно в XII веке новой эры. Однако только в XIX веке была обнаружена связь между электричеством и магнетизмом и возникло представление о магнитном поле.
Первыми экспериментами (проведены в 1820 г.), показавшими, что между электрическими и магнитными явлениями имеется глубокая связь, были опыты датского физика Х. Эрстеда. Эти опыты показали, что на магнитную стрелку, расположенную вблизи проводника с током, действуют силы, которые стремятся ее повернуть. В том же году французский физик А. Ампер наблюдал силовое взаимодействие двух проводников с токами и установил закон взаимодействия токов.
По современным представлениям, проводники с током оказывают силовое действие друг на друга не непосредственно, а через окружающие их магнитные поля.
Источниками магнитного поля являются движущиеся электрические заряды (токи). Магнитное поле возникает в пространстве, окружающем проводники с током, подобно тому, как в пространстве, окружающем неподвижные электрические заряды, возникает электрическое поле. Магнитное поле постоянных магнитов также создается электрическими микротоками, циркулирующими внутри молекул вещества (гипотеза Ампера).
Ученые XIX века пытались создать теорию магнитного поля по аналогии с электростатикой, вводя в рассмотрение так называемые магнитные заряды двух знаков (например, северный N и южный S полюса магнитной стрелки). Однако опыт показывает, что изолированных магнитных зарядов не существует.
Магнитное поле токов принципиально отличается от электрического поля. Магнитное поле, в отличие от электрического, оказывает силовое действие только на движущиеся заряды (токи).
Для описания магнитного поля необходимо ввести силовую характеристику поля, аналогичную вектору напряженности 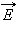 электрического поля. Такой характеристикой является вектор магнитной индукции
электрического поля. Такой характеристикой является вектор магнитной индукции 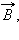 который определяет силы, действующие на токи или движущиеся заряды в магнитном поле.
который определяет силы, действующие на токи или движущиеся заряды в магнитном поле.
За положительное направление вектора 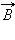 принимается направление от южного полюса S к северному полюсу N магнитной стрелки, свободно ориентирующийся в магнитном поле. Таким образом, исследуя магнитное поле, создаваемое током или постоянным магнитом, с помощью маленькой магнитной стрелки, можно в каждой точке пространства определить направление вектора
принимается направление от южного полюса S к северному полюсу N магнитной стрелки, свободно ориентирующийся в магнитном поле. Таким образом, исследуя магнитное поле, создаваемое током или постоянным магнитом, с помощью маленькой магнитной стрелки, можно в каждой точке пространства определить направление вектора  Такое исследование позволяет наглядно представить пространственную структуру магнитного поля. Аналогично силовым линиям в электростатике можно построить линии магнитной индукции, в каждой точке которых вектор
Такое исследование позволяет наглядно представить пространственную структуру магнитного поля. Аналогично силовым линиям в электростатике можно построить линии магнитной индукции, в каждой точке которых вектор 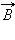 направлен по касательной. Пример линий магнитной индукции полей постоянного магнита и катушки с током приведен на рис. 1.16.1.
направлен по касательной. Пример линий магнитной индукции полей постоянного магнита и катушки с током приведен на рис. 1.16.1.

|
| Рисунок 1.16.1. Линии магнитной индукции полей постоянного магнита и катушки с током. Индикаторные магнитные стрелки ориентируются по направлению касательных к линиям индукции |
Обратите внимание на аналогию магнитных полей постоянного магнита и катушки с током. Линии магнитной индукции всегда замкнуты, они нигде не обрываются. Это означает, что магнитное поле не имеет источников – магнитных зарядов. Силовые поля, обладающие этим свойством, называются вихревыми. Картину магнитной индукции можно наблюдать с помощью мелких железных опилок, которые в магнитном поле намагничиваются и, подобно маленьким магнитным стрелкам, ориентируются вдоль линий индукции.
Для того, чтобы количественно описать магнитное поле, нужно указать способ определения не только направления вектора 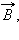 но и его модуля. Проще всего это сделать, внося в исследуемое магнитное поле проводник с током и измеряя силу, действующую на отдельный прямолинейный участок этого проводника. Этот участок проводника должен иметь длину Δl, достаточно малую по сравнению с размерами областей неоднородности магнитного поля. Как показали опыты Ампера, сила, действующая на участок проводника, пропорциональна силе тока I, длине Δl этого участка и синусу угла α между направлениями тока и вектора магнитной индукции:
но и его модуля. Проще всего это сделать, внося в исследуемое магнитное поле проводник с током и измеряя силу, действующую на отдельный прямолинейный участок этого проводника. Этот участок проводника должен иметь длину Δl, достаточно малую по сравнению с размерами областей неоднородности магнитного поля. Как показали опыты Ампера, сила, действующая на участок проводника, пропорциональна силе тока I, длине Δl этого участка и синусу угла α между направлениями тока и вектора магнитной индукции:
| F ~ IΔl sin α. |
Эта сила называется силой Ампера. Она достигает максимального по модулю значения Fmax, когда проводник с током ориентирован перпендикулярно линиям магнитной индукции. Модуль вектора 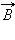 определяется следующим образом:
определяется следующим образом:
Модуль вектора магнитной индукции равен отношению максимального значения силы Ампера, действующей на прямой проводник с током, к силе тока I в проводнике и его длине Δl:
|
В общем случае сила Ампера выражается соотношением:
|
Это соотношение принято называть законом Ампера.
В системе единиц СИ за единицу магнитной индукции принята индукция такого магнитного поля, в котором на каждый метр длины проводника при силе тока 1 А действует максимальная сила Ампера 1 Н. Эта единица называется тесла (Тл).

|
Тесла – очень крупная единица. Магнитное поле Земли приблизительно равно 0,5·10–4 Тл. Большой лабораторный электромагнит может создать поле не более 5 Тл.
Сила Ампера направлена перпендикулярно вектору магнитной индукции 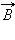 и направлению тока, текущего по проводнику. Для определения направления силы Ампера обычно используют правило левой руки: если расположить левую руку так, чтобы линии индукции
и направлению тока, текущего по проводнику. Для определения направления силы Ампера обычно используют правило левой руки: если расположить левую руку так, чтобы линии индукции 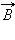 входили в ладонь, а вытянутые пальцы были направлены вдоль тока, то отведенный большой палец укажет направление силы, действующей на проводник (рис. 1.16.2).
входили в ладонь, а вытянутые пальцы были направлены вдоль тока, то отведенный большой палец укажет направление силы, действующей на проводник (рис. 1.16.2).

|
| Рисунок 1.16.2. Правило левой руки и правило буравчика |
Если угол α между направлениями вектора 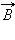 и тока в проводнике отличен от 90°, то для определения направления силы Ампера
и тока в проводнике отличен от 90°, то для определения направления силы Ампера 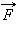 более удобно пользоваться правилом буравчика: воображаемый буравчик располагается перпендикулярно плоскости, содержащей вектор
более удобно пользоваться правилом буравчика: воображаемый буравчик располагается перпендикулярно плоскости, содержащей вектор 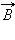 и проводник с током, затем его рукоятка поворачивается от направления тока к направлению вектора
и проводник с током, затем его рукоятка поворачивается от направления тока к направлению вектора  Поступательное перемещение буравчика будет показывать направление силы Ампера
Поступательное перемещение буравчика будет показывать направление силы Ампера 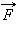 (рис. 1.16.2). Правило буравчика часто называют правилом правого винта.
(рис. 1.16.2). Правило буравчика часто называют правилом правого винта.
Одним из важных примеров магнитного взаимодействия является взаимодействие параллельных токов. Закономерности этого явления были экспериментально установлены Ампером. Если по двум параллельным проводникам электрические токи текут в одну и ту же сторону, то наблюдается взаимное притяжение проводников. В случае, когда токи текут в противоположных направлениях, проводники отталкиваются.
Взаимодействие токов вызывается их магнитными полями: магнитное поле одного тока действует силой Ампера на другой ток и наоборот.
Опыты показали, что модуль силы, действующей на отрезок длиной Δl каждого из проводников, прямо пропорционален силам тока I1 и I2 в проводниках, длине отрезка Δl и обратно пропорционален расстоянию R между ними:

|
В Международной системе единиц СИ коэффициент пропорциональности k принято записывать в виде:
| k = μ0 / 2π, |
где μ0 – постоянная величина, которую называют магнитной постоянной. Введение магнитной постоянной в СИ упрощает запись ряда формул. Ее численное значение равно
| μ0 = 4π·10–7 H/A2 ≈ 1,26·10–6 H/A2. |
Формула, выражающая закон магнитного взаимодействия параллельных токов, принимает вид:
|
Отсюда нетрудно получить выражение для индукции магнитного поля каждого из прямолинейных проводников. Магнитное поле прямолинейного проводника с током должно обладать осевой симметрией и, следовательно, замкнутые линии магнитной индукции могут быть только концентрическими окружностями, располагающимися в плоскостях, перпендикулярных проводнику. Это означает, что векторы  и
и 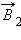 магнитной индукции параллельных токов I1 и I2 лежат в плоскости, перпендикулярной обоим токам. Поэтому при вычислении сил Ампера, действующих на проводники с током, в законе Ампера нужно положить sin α = 1. Из закона магнитного взаимодействия параллельных токов следует, что модуль индукции B магнитного поля прямолинейного проводника с током I на расстоянии R от него выражается соотношением
магнитной индукции параллельных токов I1 и I2 лежат в плоскости, перпендикулярной обоим токам. Поэтому при вычислении сил Ампера, действующих на проводники с током, в законе Ампера нужно положить sin α = 1. Из закона магнитного взаимодействия параллельных токов следует, что модуль индукции B магнитного поля прямолинейного проводника с током I на расстоянии R от него выражается соотношением
|
Для того, чтобы при магнитном взаимодействии параллельные токи притягивались, а антипараллельные отталкивались, линии магнитной индукции поля прямолинейного проводника должны быть направлены по часовой стрелке, если смотреть вдоль проводника по направлению тока. Для определения направления вектора 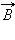 магнитного поля прямолинейного проводника также можно пользоваться правилом буравчика: направление вращения рукоятки буравчика совпадает с направлением вектора
магнитного поля прямолинейного проводника также можно пользоваться правилом буравчика: направление вращения рукоятки буравчика совпадает с направлением вектора 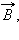 если при вращении буравчик перемещается в направлении тока (рис. 1.16.3).
если при вращении буравчик перемещается в направлении тока (рис. 1.16.3).

|
| Рисунок 1.16.3. Магнитное поле прямолинейного проводника с током |

|
| Рисунок 1.16.4. Магнитное взаимодействие параллельных и антипараллельных токов |
Рис. 1.16.4 поясняет закон взаимодействия параллельных токов.
Магнитное взаимодействие параллельных проводников с током используется в Международной системе единиц (СИ) для определения единицы силы тока – ампера:
Ампер – сила неизменяющегося тока, который при прохождении по двум параллельным проводникам бесконечной длины и ничтожно малого кругового сечения, расположенным на расстоянии 1 м один от другого в вакууме, вызвал бы между этими проводниками силу магнитного взаимодействия, равную 2·10–7 Н на каждый метр длины.
1.17. Закон Био–Савара. Теорема о циркуляции
Магнитное поле постоянных токов различной конфигурации изучалось экспериментально французскими учеными Ж. Био и Ф. Саваром (1820 г.). Они пришли к выводу, что индукция магнитного поля токов, текущих по проводнику, определяется совместным действием всех отдельных участков проводника. Магнитное поле подчиняется принципу суперпозиции:
Если магнитное поле создается несколькими проводниками с током, то индукция результирующего поля есть векторная сумма индукций полей, создаваемых каждым проводником в отдельности.
Индукцию  проводника с током можно представить как векторную сумму элементарных индукций
проводника с током можно представить как векторную сумму элементарных индукций  создаваемых отдельными участками проводника. На опыте невозможно выделить отдельный участок проводника с током, так как постоянные токи всегда замкнуты. Можно измерить только суммарную индукцию магнитного поля, создаваемого всеми элементами тока. Закон Био–Савара определяет вклад
создаваемых отдельными участками проводника. На опыте невозможно выделить отдельный участок проводника с током, так как постоянные токи всегда замкнуты. Можно измерить только суммарную индукцию магнитного поля, создаваемого всеми элементами тока. Закон Био–Савара определяет вклад  в магнитную индукцию
в магнитную индукцию  результирующего магнитного поля, создаваемый малым участком Δl проводника с током I.
результирующего магнитного поля, создаваемый малым участком Δl проводника с током I.
|
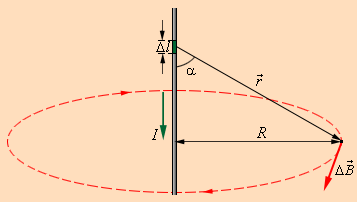
Здесь r – расстояние от данного участка Δl до точки наблюдения, α – угол между направлением на точку наблюдения и направлением тока на данном участке, μ0 – магнитная постоянная. Направление вектора  определяется правилом буравчика: оно совпадает с направлением вращения рукоятки буравчика при его поступательном перемещении вдоль тока. Рис. 1.17.1 иллюстрирует закон Био–Савара на примере магнитного поля прямолинейного проводника с током. Если просуммировать (проинтегрировать) вклады в магнитное поле всех отдельных участков прямолинейного проводника с током, то получится формула для магнитной индукции поля прямого тока:
определяется правилом буравчика: оно совпадает с направлением вращения рукоятки буравчика при его поступательном перемещении вдоль тока. Рис. 1.17.1 иллюстрирует закон Био–Савара на примере магнитного поля прямолинейного проводника с током. Если просуммировать (проинтегрировать) вклады в магнитное поле всех отдельных участков прямолинейного проводника с током, то получится формула для магнитной индукции поля прямого тока:
|
которая уже приводилась в § 1.16.
|
| Рисунок 1.17.1. Иллюстрация закона Био–Савара |
Закон Био–Савара позволяет рассчитывать магнитные поля токов различных конфигураций. Нетрудно, например, выполнить расчет магнитного поля в центре кругового витка с током. Этот расчет приводит к формуле
|
где R – радиус кругового проводника. Для определения направления вектора  также можно использовать правило буравчика, только теперь его рукоятку нужно вращать в направлении кругового тока, а поступательное перемещение буравчика укажет направление вектора магнитной индукции.
также можно использовать правило буравчика, только теперь его рукоятку нужно вращать в направлении кругового тока, а поступательное перемещение буравчика укажет направление вектора магнитной индукции.
Расчеты магнитного поля часто упрощаются при учете симметрии в конфигурации токов, создающих поле. В этом случае можно пользаоваться теоремой о циркуляции вектора магнитной индукции, которая в теории магнитного поля токов играет ту же роль, что и теорема Гаусса в электростатике.
Поясним понятие циркуляции вектора  Пусть в пространстве, где создано магнитное поле, выбран некоторый условный замкнутый контур (не обязательно плоский) и указано положительное направление его обхода. На каждом отдельном малом участке Δl этого контура можно определить касательную составляющую
Пусть в пространстве, где создано магнитное поле, выбран некоторый условный замкнутый контур (не обязательно плоский) и указано положительное направление его обхода. На каждом отдельном малом участке Δl этого контура можно определить касательную составляющую 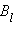 вектора
вектора 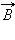 в данном месте, то есть определить проекцию вектора
в данном месте, то есть определить проекцию вектора 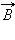 на направление касательной к данному участку контура (рис. 1.17.2).
на направление касательной к данному участку контура (рис. 1.17.2).

|
| Рисунок 1.17.2. Замкнутый контур (L) с заданным направлением обхода. Изображены токи I1, I2 и I3, создающие магнитное поле |
Циркуляцией вектора 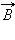 называют сумму произведений
называют сумму произведений 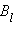 Δl, взятую по всему контуру L:
Δl, взятую по всему контуру L:

|
Некоторые токи, создающие магнитное поле, могут пронизывать выбранный контур L в то время, как другие токи могут находиться в стороне от контура.
Теорема о циркуляции утверждает, что циркуляция вектора 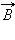 магнитного поля постоянных токов по любому контуру L всегда равна произведению магнитной постоянной μ0 на сумму всех токов, пронизывающих контур:
магнитного поля постоянных токов по любому контуру L всегда равна произведению магнитной постоянной μ0 на сумму всех токов, пронизывающих контур:
|
В качестве примера на рис. 1.17.2 изображены несколько проводников с токами, создающими магнитное поле. Токи I2 и I3 пронизывают контур L в противоположных направлениях, им должны быть приписаны разные знаки – положительными считаются токи, которые связаны с выбранным направлением обхода контура правилом правого винта (буравчика). Следовательно, I3 > 0, а I2 < 0. Ток I1 не пронизывает контур L.
Теорема о циркуляции в данном примере выражается соотношением:

|
Теорема о циркуляции в общем виде следует из закона Био–Савара и принципа суперпозиции.
Простейшим примером применения теоремы о циркуляции является вывод формулы для магнитной индукции поля прямолинейного проводника с током. Учитывая симметрию в данной задаче, контур L целесообразно выбрать в виде окружности некоторого радиуса R, лежащей в перпендикулярной проводнику плоскости. Центр окружности находится в некоторой точке проводника. В силу симметрии вектор 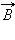 направлен по касательной
направлен по касательной 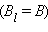 , а его модуль одинаков во всех точках окружности. Применение теоремы о циркуляции приводит к соотношению:
, а его модуль одинаков во всех точках окружности. Применение теоремы о циркуляции приводит к соотношению:

|
откуда следует формула для модуля магнитной индукции поля прямолинейного проводника с током, приведенная ранее.
Этот пример показывает, что теорема о циркуляции вектора магнитной индукции 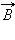 может быть использована для расчета магнитных полей, создаваемых симметричным распределением токов, когда из соображений симметрии можно «угадать» общую структуру поля.
может быть использована для расчета магнитных полей, создаваемых симметричным распределением токов, когда из соображений симметрии можно «угадать» общую структуру поля.
Имеется немало практически важных примеров расчета магнитных полей с помощью теоремы о циркуляции. Одним из таких примеров является задача вычисления поля тороидальной катушки (рис. 1.17.3).

|
| Рисунок 1.17.3. Применение теоремы о циркуляции к тороидальной катушке |
Предполагается, что катушка плотно, то есть виток к витку, намотана на немагнитный тороидальный сердечник. В такой катушке линии магнитной индукции замыкаются внутри катушки и представляют собой концентрические окружности. Они направлены так, что глядя вдоль них, мы увидели бы ток в витках, циркулирующим по часовой стрелке. Одна из линий индукции некоторого радиуса r1 ≤ r < r2 изображена на рис. 1.17.3. Применим теорему о циркуляции к контуру L в виде окружности, совпадающей с изображенной на рис. 1.17.3 линией индукции магнитного поля. Из соображений симметрии ясно, что модуль вектора 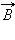 одинаков вдоль всей этой линии. По теореме о циркуляции можно записать:
одинаков вдоль всей этой линии. По теореме о циркуляции можно записать:
| B ∙ 2πr = μ0IN, |
где N – полное число витков, а I – ток, текущий по виткам катушки. Следовательно,
|
Таким образом, модуль вектора магнитной индукции в тороидальной катушке зависит от радиуса r. Если сердечник катушки тонкий, то есть r2 – r1 << r, то магнитное поле внутри катушки практически однородно. Величина n = N / 2πr представляет собой число витков на единицу длины катушки. В этом случае
|
В это выражение не входит радиус тора, поэтому оно справедливо и в предельном случае r → ∞. Но в пределе каждую часть тороидальной катушки можно рассматривать как длинную прямолинейную катушку. Такие катушки называют соленоидами. Вдали от торцов соленоида модуль магнитной индукции выражается тем же соотношением, что и в случае тороидальной катушки.
На рис. 1.17.4 изображено магнитное поле катушки конечной длины. Следует обратить внимание на то, что в центральной части катушки магнитное поле практически однородно и значительно сильнее, чем вне катушки. На это указывает густота линий магнитной индукции. В предельном случае бесконечно длинного соленоида однородное магнитное поле целиком сосредоточено внутри него.

|
| Рисунок 1.17.4. Магнитное поле катушки конечной длины. В центре соленоида магнитное поле практически однородно и значительно превышает по модулю поле вне катушки |
В случае бесконечно длинного соленоида выражение для модуля магнитной индукции можно получить непосредственно с помощью теоремы о циркуляции, применив ее к прямоугольному контуру, показанному на рис. 1.17.5.

|
| Рисунок 1.17.5. Применение теоремы о циркуляции к расчету магнитного поля бесконечно длинного соленоида |
Вектор магнитной индукции имеет отличную от нуля проекцию на направление обхода контура abcd только на стороне ab. Следовательно, циркуляция вектора 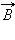 по контуру равна Bl, где l – длина стороны ab. Число витков соленоида, пронизывающих контур abcd, равно n · l, где n – число витков на единицу длины соленоида, а полный ток, пронизывающий контур, равен I n l. Согласно теореме о циркуляции,
по контуру равна Bl, где l – длина стороны ab. Число витков соленоида, пронизывающих контур abcd, равно n · l, где n – число витков на единицу длины соленоида, а полный ток, пронизывающий контур, равен I n l. Согласно теореме о циркуляции,
| B l = μ0I n l, |
откуда
|
Это выражение совпадает с полученной ранее формулой для магнитного поля тонкой тороидальной катушки.
Date: 2015-12-10; view: 972; Нарушение авторских прав