Кривые второго порядка

Рассмотрим линии, определяемые уравнениями второй степени относительно текущих координат

. (2.41)

Коэффициенты уравнения - действительные числа, но по крайней мере одно из чисел А, В или С отлично от нуля. Такие линии называются кривыми второго порядка.

Установим при каких условиях уравнение (2.41) определяет окружность, эллипс, гиперболу или параболу.

Определение. Окружность называется геометрическое место точек плоскости, равноудаленных от данной точки (центра).

Если R - радиус окружности, а точка - ее центр, то уравнение окружности имеет вид:

. (2.42)

В частности, если центр окружности совпадает с началом координат, то последнее уравнение имеет вид:

(2.43)

Уравнение окружности (2.42) после несложных преобразований примет вид . При сравнении этого уравнения с общим уравнением (2.41) кривой второго порядка легко заметить, что для уравнения окружности выполнены два условия:

1) коэффициенты при и равны между собой (А=С);

2) отсутствует член, содержащий произведение ху текущих координат, то есть В=0.

Пример 31. Найти координаты центра и радиус окружности .

Решение. Разделим данное уравнение на 2: или .

Дополним и до полных квадратов:

,

.

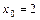Тогда данное уравнение примет вид: , или . Таким образом, координаты центра окружности , и радиус окружности .

Пример 32. Составить уравнение окружности, проходящей через точки , , .

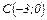Решение. Для составления уравнения окружности найдем координаты центра и радиус окружности. По условию искомая окружность проходит через три данные точки, поэтому в уравнение (2.42) подставим поочередно координаты этих точек вместо х и у:

: ,

: ,

: .

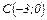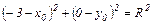Получили три уравнения с тремя неизвестными. Для нахождения этих неизвестных решим систему уравнений:

Так как правые части всех уравнений равны, приравниваем левые так, чтобы получить два уравнения с двумя неизвестными

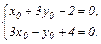
Умножим второе уравнение на 3 и прибавим к первому, получим ,

Тогда , . Значит центром окружности является точка . Подставив найденные координаты центра в любое из уравнений (например, второе) первой системы найдем :

, значит . Таким образом, уравнение искомой окружности имеет вид: .

Определение. Эллипсом называется геометрическое место точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная (ее обозначают обычно через 2а), причем эта постоянная больше расстояния между фокусами.

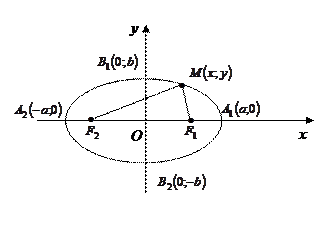
Если оси координат расположены по отношению к эллипсу так, как на рисунке, а фокусы эллипса находятся на оси Ох на равных расстояниях от начала координат в точках и , то уравнение эллипса принимает простейший (так называемый канонический) вид

. (2.44)

Здесь а - большая, b - малая полуоси эллипса, причем а, b и с (с - половина расстояния между фокусами) связаны соотношением

(2.45)

Точки пересечения эллипса с осями координат , , и называются вершинами эллипса, точка - центром эллипса, а оси координат - осями симметрии эллипса, ось на которой расположены фокусы, - фокальной осью. называется правым фокусом, а - левым.

Форма эллипса (мера его сжатия) характеризуется его эксцентриситетом 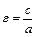(так как , то ): чем меньше эксцентриситет, тем меньше его малая полуось b отличается от большой полуоси а, то есть тем меньше вытянут эллипс вдоль фокальной оси. Если положить (а это значит, что с=0, b=a), то эллипс превращается в окружность. Таким образом, общее уравнение кривой второго порядка (2.41) может быть уравнением эллипса, если коэффициенты А и С одного знака, а В=0.

Пример 33. Эллипс, симметричный относительно осей координат, проходит через точку и имеет эксцентриситет . Составить уравнение эллипса.

Решение. Так как эллипс проходит через точку , то координаты этой точки удовлетворяют уравнению (2.44) или . Эксцентриситет эллипса 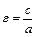, а по условию , поэтому , , 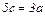. Используя равенство (2.45), получаем , , .

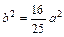Решим систему уравнений относительно и :

Так как , тогда , , , тогда .

Таким образом, искомое уравнение эллипса принимает вид

или

Пример 34. Составить уравнение прямой, проходящей через левый фокус и нижнюю вершину эллипса .

Решение. Левый фокус эллипса - . Найдем с из условия (2.45), зная, что , :

, , .

Значит левый фокус эллипса - .

Нижняя вершина эллипса . По условию , поэтому . Пользуясь уравнением (2.30), составим уравнение искомой прямой

, , или .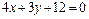

Определение. Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная (равная 2а), меньшая, чем расстояние между фокусами.

Поместив фокусы гиперболы в точках (правый фокус) и (левый фокус) и расположив оси координат по отношению к гиперболе так, как на рисунке, получаем простейшее (каноническое) уравнение гиперболы в виде

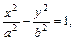(2.46)

где а, b и с связаны соотношением

. (2.47)

Гипербола состоит из двух ветвей и расположена симметрично относительно осей координат. Точки и называются вершинами гиперболы. Отрезок 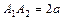называют вещественной осью гиперболы, а отрезок - мнимой осью. Ось, на которой расположены фокусы, называется фокальной осью.

Определение. Прямая называется асимптотой гиперболы, если расстояние точки гиперболы от этой прямой стремится к нулю при или . Гипербола имеет две асимптоты, уравнения которых

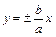. (2.48)

Для построения асимптот гиперболы строят осевой (основной) прямоугольник гиперболы со сторонами , , 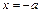, . Прямые, проходящие через противоположные вершины этого прямоугольника, являются асимптотами гиперболы. Точка называется центром гиперболы.

Форма гиперболы характеризуется его эксцентриситетом 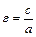(так как 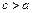, то ). Чем меньше эксцентриситет гиперболы, тем более вытянут ее основной прямоугольник и наоборот. Гипербола называется равносторонней (равнобочной), если ее полуоси равны (а=b). Её каноническое уравнение

(2.49)

Асимптоты равносторонней гиперболы имеют уравнения , следовательно являются биссектрисами координатных углов. Эксцентриситет равносторонней гиперболы равен .

Уравнение

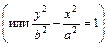(2.50)

также является уравнением гиперболы, но вещественной осью этой гиперболы служит отрезок оси Оу длины 2b. Две гиперболы и имеют одни и те же полуоси и одни и те же асимптоты, но вещественная ось одной служит мнимой осью другой, и наоборот. Такие две гиперболы называются сопряженными. Итак, общее уравнение кривой второго порядка (2.41) может быть уравнением гиперболы, если коэффициенты А и С разных знаков, а В=0.

Пример 35. Составить уравнение гиперболы, проходящей через точку 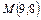, если асимптоты гиперболы имеют уравнения . Построить гиперболу.

Решение. Так как гипербола проходит через точку 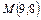, то ее координаты удовлетворяют уравнению (2.46)

, , .

Уравнения асимптот имеют вид (2.48), а по условию задачи , приравнивая правые части этих уравнений, получаем:

, , .

Таким образом, получили систему уравнений:

, , .

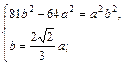
Так как , тогда , , , значит , , .

Таким образом, искомое уравнение гиперболы имеет вид .

Для построения гиперболы, построим основной прямоугольник, стороны которого задаются уравнениями , , 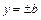то есть , .

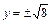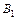Уравнения асимптот гиперболы даны по условию . Вершины гиперболы , . Точки 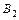и : и . Найдем координаты фокусов, пользуясь соотношением (2.47) . Значит левый фокус гиперболы , а правый - .

Используя полученные результаты, выполним построения.

Пример 36. Через точку и правую вершину гиперболы 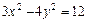проведена прямая. Найти вторую точку пересечения прямой с гиперболой.

Решение. Преобразуем данное уравнение гиперболы к виду (2.46):

, .

Правая вершина гиперболы . По условию , поэтому 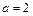, значит .

Найдем уравнение данной прямой, пользуясь уравнением прямой, проходящей через две точки (2.30).

, , , ,

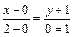то есть уравнение прямой .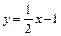

Для нахождения второй точки пересечения прямой с гиперболой, решим систему уравнений

, ,

, .

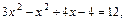
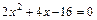Найдем вторые координаты , , , .

Таким образом получили две точки: и . Но точка совпадает с правой вершиной гиперболы , поэтому искомой точкой является .

Определение. Параболой называется множество всех точек плоскости каждая из которых одинаково удалена от данной точки, называемой фокусом, и данной прямой, называемой директрисой. Расстояние от фокуса F до директрисы называется параметром параболы и обозначается через .

Если выбрать систему координат Оху так, чтобы ось Ох проходила через фокус F перпендикулярно директрисе в направлении от директрисы к F, а начало координат О расположить посередине между фокусом и директрисой, причем фокус F имеет координаты , уравнение директрисы - или , то уравнение параболы будет иметь вид

. (2.51)

Уравнение (2.51) называется каноническим уравнением параболы.

В выбранной системе координат ось Ох является осью симметрии параболы.

Так как 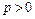, то уравнение (2.51) имеет смысл при , следовательно парабола расположена справа от оси Оу.

При имеем . Следовательно, пfрабола проходит через начало координат. Точка называется вершиной параболы.

При другом выборе системы координат получаются канонические уравнения другого вида

, (2.52)

, (2.53)

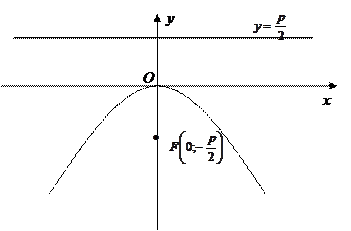
, . (2.54)

Пример 37. Составить каноническое уравнение параболы, если известно, что ее фокус находится в точке пересечения прямой с осью Ох.

Решение. Найдем точку пересечения данной прямой с осью Ох, координаты которой являются координатами фокуса F искомой параболы. На оси Ох любая точка имеет ординату , поэтому из уравнения прямой при этом условии найдем х: 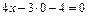, , . Значит фокус пораболы , тогда , 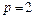. Так как фокус расположен справа от начала координат, тогда искомое уравнение параболы будет иметь вид (2.51):

или .

Пример 38. Составить уравнение параболы с вершиной в начале координат, симметричной относительно оси Ох и отсекающей от прямой хорду длиной .

Решение. Прямая проходит через начало координат , так как является биссектрисой I и II координатных углов. Искомая парабола симметрична относительно оси Ох, поэтому уравнение параболы может иметь вид или . Рассмотрим каждый из этих случаев. Если , то вторая точка пересечения прямой с параболой , , 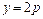значит и , то есть точка . Длина хорды определяется как расстояние между двумя точками и : , , , 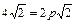тогда 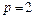, а значит искомое уравнение параболы

.

Рассмотрим второй случай, когда уравнение параболы имеет вид . Найдем точки пересечения параболы и данной прямой.

, , , , . Получили две точки и .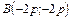

Далее, рассуждая аналогично первому случаю, получаем: , , 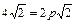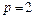. Тогда искомое уравнение параболы .

Таким образом, условиям задачи удовлетворяют два уравнения параболы: и .

Можно сделать вывод, что общее уравнение кривой второго порядка (2.41) может быть уравнением параболы, если коффициенты , или , , то есть одна из переменных должна быть в первой степени.

Но не всякое уравнение вида (2.41) определяет кривую второго порядка. Например, не существует точек плоскости, удовлетворяющих уравнению .

Date: 2015-12-10; view: 749; Нарушение авторских прав