Ранг матрицы

Рассмотрим матрицу А размера

.

Выделим в ней k строк и k столбцов 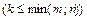. Из элементов, стоящих на пересечении выделенных строк и столбцов, составим определитель k -го порядка. Все такие определители называются минорами этой матрицы.

Определение. Рангом матрицы А называется наибольший из порядков миноров данной матрицы, отличных от нуля.

Обозначают ранг матрицы или .

Пример 28. Найти ранг матрицы:

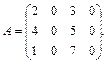
Решение. Дана матрица размера . Возможный ранг матрицы равен трем, т.к. 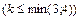. Но матрица содержит два нулевых столбца, поэтому все определители третьего порядка, составленные из элементов данной матрицы равны нулю:

, , .

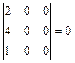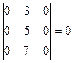Составим минор второго порядка, например

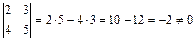. Значит,

Ранг матрицы удобно вычислять, используя элементарные преобразования над матрицей. К элементарным относятся следующие преобразования:

1) перестановка местами двух параллельных рядов матрицы;

2) умножение всех элементов ряда матрицы на число, отличное от нуля;

3) прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число.

Определение. Две матрицы А и В называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований. Записывается 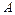~ В.

Свойства ранга матрицы:

1. При транспонировании матрицы ее ранг не меняется.

2. Ранг матрицы не изменится, если вычеркнуть из матрицы нулевой ряд.

3. При элементарных преобразованиях ранг матрицы не изменяется, т.е. если 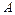~ В, то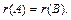

Пример 29. Найти ранг матрицы

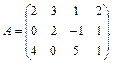
Решение. Умножим элементы первой строки на (-2) и прибавим к элементам третьей строки

~

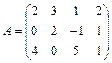Элементы второй строки умножим на 3 и прибавим к элементам третьей строки

~

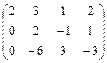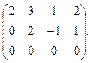
Вычеркнем третью строку полученной матрицы, т.к. все ее элементы равны нулю:

~ .

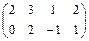Составим минор второго порядка:

.

Таким образом,

В преобразованной матрице получилось две ненулевые строки.

Пример 30. Найти ранг матрицы

.

Решение. Умножим элементы первой строки на (-2) и прибавим к элементам второй строки данной матрицы:

~ .

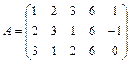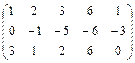Умножим элементы первой строки на (-3) и прибавим к элементам третьей строки:

~ .

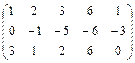Элементы второй строки полученной матрицы умножим на (-5) и прибавим к элементам третьей строки:

~

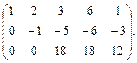
Из элементов полученной матрицы составим определитель третьего порядка. Для этого возьмем первые три столбца:

.

Получили определитель треугольного вида, значение которого равно произведению элементов главной диагонали

.

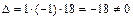Ранг последней матрицы равен 3, следовательно ранг данной матрицы тоже равен 3.

В последней матрице содержится три ненулевые строки.

Можно сделать следующий вывод:

ранг матрицы равен количеству ненулевых строк преобразованной к треугольному виду матрицы.

Date: 2015-12-10; view: 332; Нарушение авторских прав