Основы расчета статически неопределимых систем методом сил

Система называется статически неопределимой, если усилия в ее элементах невозможно определить только из уравнений равновесия.

Количество лишних связей в заданной системе определим по формуле:

где К – количество замкнутых контуров в системе, Ш – число простых шарниров.

Шарнир называется простым или одиночным, если он связывает два элемента (рис.25.1, а).

Если шарнир связывает n элементов, то он называется кратным или общим (рис.25.1, б).

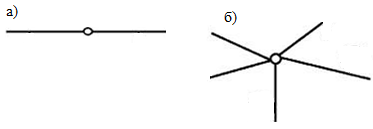
Рис. 25.1. Схема одиночного и кратного шарниров

Кратный шарнир эквивалентен n – 1 простым шарнирам.

С другой стороны

где число опорных связей; число простых шарниров; количество дисков в системе.

Для рамы, изображенной на рис. 25.2, построить эпюры внутренних усилий М, Q и N.

Для заданной системы определим степень статической неопределимости по формуле:

.

Данная система является дважды статически неопределимой, т. е. имеет две лишние связи. Рассмотрим статически определимую систему, полученную из заданной системы удалением лишних связей. Такая

система называется основной (О. С.).

Удалим опорные связи на опоре А и получим основную систему, изображенную на рис. 25.2, б. Основная система, загруженная внешней нагрузкой и лишними неизвестными, называется эквивалентной системой (Э. С.) (рис. 25.2, в). Эквивалентная система будет эквивалентной заданной только при тех значениях неизвестных Х₁ и Х₂, при которых горизонтальное ∆₁ и вертикальное ∆₂ перемещения точки А равны нулю, т. е.:

Рис. 25.2. Схема статически неопределимой рамы

При вычислении перемещений, когда используем принцип независимости действия сил, тогда

где – перемещение в основной системе по направлению силы , вызванное силой F.

Для упругих линейно-деформируемых систем имеем:

где перемещение в основной системе по направлению силы , вызванное силой

Условия совместности деформаций для заданной системы можно представить системой канонических уравнений в виде:

Общие свойства системы канонических уравнений:

1. Это система линейных алгебраических уравнений;

2. Уравнений в системе столько, сколько раз она статически неопределимая;

3. В каждое уравнение входит не более чем n неизвестных, где n – степень статической неопределимости системы;

4. Коэффициенты уравнений не зависят от внешней нагрузки. Они полностью определяются свойствами основной системы.

Коэффициенты и свободные члены , канонических уравнений являются перемещениями в основной статически определимой системе. Для их определения воспользуемся методом Мора, т. е.:

где и – перемещения в основной системе по направлению силы , вызванные силой и внешней нагрузкой F соответственно. и – побочные коэффициенты и свободные члены канонических уравнений метода сил соответственно.

Коэффициенты, которые имеют одинаковые индексы, называются главными коэффициентами канонических уравнений.

Главные коэффициенты всегда имеют положительное значение.

В балках и рамах для определения коэффициентов и свободных членов канонических уравнений удобно пользоваться способом Верещагина, т. е.:

.

Определим коэффициенты и свободные члены канонических уравнений для рассматриваемого примера. Для этого построим эпюры изгибающих моментов в основной системе от действия единичных лишних неизвестных и внешней нагрузки (рис.25.2, а, б, в).

Рис. 25.3. Эпюры изгибающих моментов в основной системе

Подставив найденные коэффициенты в систему канонических уравнений, получим:

После несложных преобразований имеем:

Решая последнюю систему уравнений методом исключений, находим:

Знак минус в выражениях для указывает на то, что истинное направление неизвестного усилия противоположно первоначально принятому направлению.

Для построения суммарной эпюры изгибающих моментов обычно используют принцип независимости действия сил, согласно которому суммарный изгибающий момент в любом сечении можно вычислить по формуле:

Для рассматриваемого примера сложение эпюр выполнено на рис.25.4.

Рис. 25.4. Построение суммарной эпюры М

После построения суммарной эпюры изгибающих моментов вычисляем поперечные силы, рассматривая равновесия отдельных участков рамы. Суммарная эпюра Q изображена на рис. 25.6, а

Рассмотрим произвольный участок рамы АВ, на котором по всей длине действует равномерно распределенная нагрузка q (рис. 25.5, а).

Рис. 25.5.Схема для определения

поперечных сил на произвольном

участке рамы

где балочная поперечная сила.

На участке, где отсутствует равномерно распределенная нагрузка q, формула для определения поперечной силы имеет вид:

По суммарной эпюре изгибающих моментов (рис. 25.4, г) строим эпюру поперечных сил Q (рис. 25.6, а).

Рис. 25.6. Построение эпюр поперечных и продольных сил

Вырезая узел С на эпюре Q и рассматривая его равновесие (рис. 25.6, б) строим эпюру N (рис. 25.6, в).

Date: 2015-12-10; view: 1343; Нарушение авторских прав