Контрольная работа № 2. 201. Бесконечно длинный провод с током I = 100 А изогнут так, как это показано на рис.2.1

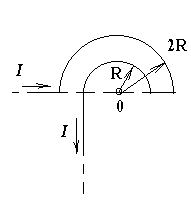
201. Бесконечно длинный провод с током I = 100 А изогнут так, как это показано на рис.2.1. Определить магнитную индукцию В в точке О. Радиус дуги R = 10 см.

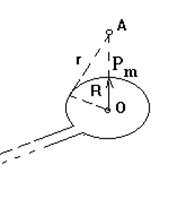
202. Магнитный момент р_m тонкого проводящего кольца p_m = 5 А×м². Определить магнитную индукцию В в точке А, находящейся на оси кольца и удаленной от кольца на расстояние r = 20 см (рис.2.2).

203. По двум скрещенным под прямым углом бесконечно длинным проводам текут токи I и 2 I (I = 100 А). Определить магнитную индукцию В в точке А (рис.2.3). Расстояние d = 10 см.

204. По бесконечно длинному проводу, изогнутому так, как показано на рис.2.4, течет ток I = 200 А. Определить магнитную индукцию В в точке О. Радиус дуги R = 10 см.

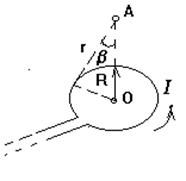
205. По тонкому кольцу радиусом R = 20 см течет ток I = 100 А. Определить магнитную индукцию В на оси кольца в точке А (рис.2.5). Угол b = p/3.

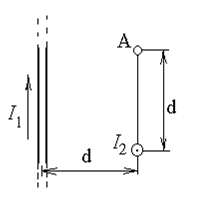
206. По двум бесконечно длинным проводам, скрещенным под прямым углом, текут токи I₁ и I₂ = 2 I₁ (I₁ = 100 А). Определить магнитную индукцию В в точке А, равноудаленной от проводов на расстояние d = 10 см (рис.2.6).

207. По бесконечно длинному проводу, изогнутому так, как показано на рис. 2.8, течет ток I = 200 А. Определить магнитную индукцию В в точке О. Радиус дуги R = 10 см.

208. По тонкому кольцу течет ток I = 80 А. Определить магнитную индукцию В в точке А, равноудаленной от точек кольца на расстояние r = 10 см (рис.2.7). Угол a = p/6.

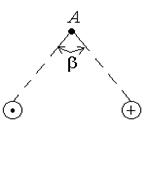
209. По двум бесконечно длинным прямым, параллельным проводам, текут одинаковые токи I = 60 А. Определить магнитную индукцию В в точке А (рис.2.9), равноудаленной от проводов на расстояние d = 10 см. Угол b = p/3.

210. Бесконечно длинный провод с током I = 60 А изогнут так, как показано на рис.2.10. Определить магнитную индукцию В в точке А, лежащей на биссектрисе прямого угла на расстоянии d = 10 см от его вершины.

211. Протон, прошедший ускоряющую разность потенциалов U =800 В, влетел в однородное магнитное поле с индукцией В = 0,06 Тл и начал двигаться по окружности. Найти её радиус.

212. Однозарядный ион прошел ускоряющую разность потенциалов U = 1 кВ и влетел перпендикулярно линиям магнитной индукции в однородное поле (В = 0,5 Тл). Определить массу m иона, если он описал окружность радиусом R = 4,37 см.

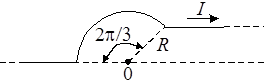
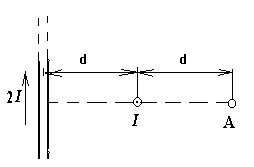Рис. 2.3 Рис. 2.4

Рис. 2.1 Рис. 2.2

Рис. 2.5 Рис. 2.6

Рис. 2.7 Рис. 2.8

Рис. 2.9 Рис. 2.10

213. Электрон, ускоренный разностью потенциалов U = 500 В движется параллельно прямолинейно длинному проводу на расстоянии d = 5 мм от него. Найти силу F, действующую на электрон, если по проводу пустить ток I =10 А.

214. Альфа-частица прошла ускоряющую разность потенциалов U = 300 В и, попав в однородное магнитное поле, стала двигаться по винтовой линии радиусом R = 1 см и шагом h = 4 мм. Определить магнитную индукцию В поля.

215. Заряженная частица прошла ускоряющую разность потенциалов U = 100 В и, влетев в однородное магнитное поле (В = 0,1 Тл), стала двигаться по винтовой линии с шагом h = 6,5 см и радиусом R = 1 см. Определить отношение заряда частицы к ее массе.

216. Протон и электрон, ускоренные одинаковой разностью потенциалов, влетают в однородное магнитное поле. Во сколько радиус кривизны R₁ траектории протона больше радиуса кривизны R₂ траектории электрона?

217. Протон прошел ускоряющую разность потенциалов U = 800 В и влетел в однородное магнитное поле (В = 20 мТл) под углом a = 30° к линиям магнитной индукции. Определить шаг h и радиус R винтовой линии, по которой будет двигаться протон в магнитном поле.

218. Альфа-частица, пройдя ускоряющую разность потенциалов U, стала двигаться в однородном магнитном поле (В = 50 мТл) по винтовой линии с шагом h = 5 см и радиусом R = 1 см. Определить ускоряющую разность потенциалов, которую прошла альфа-частица.

219. Заряженная частица со скоростью v =10⁶ м/с влетев в однородное магнитное поле с индукцией В = 0,3 Тл и стала двигаться по окружности радиусом R = 4 см. Найти заряд Q частицы, если её кинетическая энергия Т = 12 кэВ.

220. Заряженная частица с энергией Т = 1 кэВ движется в однородном магнитном поле по окружности радиусом R = 1,4 мм. Найти силу F, действующую на частицу со стороны поля.

221. В однородном магнитном поле с индукцией В = 0,8 Тл находится прямой провод длиной l = 30 cм, концы которого замкнуты вне поля. Сопротивление всей цепи R = 0,2 Ом. Найти силу, которую нужно приложить к проводу, чтобы перемещать его перпендикулярно линиям индукции со скоростью v = 2,5 м/с.

222. В однородном магнитном поле с индукцией В = 0,5 Тл вращается с частотой n = 5 с^-1 стержень длиной l = 20 см. Ось вращения параллельна линиям индукции и проходит через один из концов стержня перпендикулярно его оси. Определить разность потенциалов U на концах стержня.

223. Тонкий медный провод массой m = 5 г согнут в виде квадрата, и концы его замкнуты. Квадрат помещен в однородное магнитное поле (В = 0,2 Тл) так, что плоскость перпендикулярна линиям поля. Определить заряд Q, который потечет по проводнику, если квадрат, потянув за противоположные вершины, вытянуть в линию.

224. Рамка, содержащая N = 200 витков тонкого провода, может свободно вращаться относительно оси, лежащей в плоскости рамки. Площадь рамки S = 50 см². Ось рамки перпендикулярна линиям индукции магнитного поля (В = 0,05 Тл). Определить максимальную ЭДС e_max, которая индуцируется в рамке при ее вращении с частотой n = 40 с^-1.

225. Прямой проводящий стержень длиной l = 40 см находится в однородном магнитном поле (В = 0,1 Тл). Концы стержня замкнуты гибким проводом, находящимся вне поля. Сопротивление всей цепи R = 0,5 Ом. Какая мощность Р потребуется для равномерного перемещения стержня перпендикулярно линиям магнитной индукции со скоростью V = 10 м/с?

226. Проволочный контур площадью S = 500 см² и сопротивлением R = 0,1 Ом равномерно вращается в однородном магнитном поле (В = 0,5 Тл). Ось вращения лежит в плоскости кольца и перпендикулярна линиям магнитной индукции. Определить максимальную мощность Р_max, необходимую для вращения контура с угловой скоростью w = 50 рад/с.

227. Соленоид содержит N = 800 витков. Сечение сердечника (из немагнитного материала) S = 10 см². По обмотке течет ток, создающий поле с индукцией В = 8 мТл. Определить среднее значение ЭДС < e_S > самоиндукции, которая возникает на зажимах соленоида, если сила тока уменьшается практически до нуля за время Dt = 0,8 мс.

228. В электрической цепи, содержащей резистор сопротивлением R = 20 Ом и катушку индуктивностью L = 0,06 Гн, течет ток I = 20 А. Определить силу тока I в цепи через Dt = 0,2 мс после ее размыкания.

229. Цепь состоит из катушки индуктивностью L = 0,1 Гн и источника тока. Источник тока отключили, не разрывая цепи. Время, через которое сила тока уменьшится до 0,001 первоначального значения, равно t = 0,07 с. Определить сопротивление катушки.

230. Источник тока замкнули на катушку сопротивлением R = 10 Ом и индуктивностью L = 0,2 Гн. Через какое время сила тока в цепи достигнет 50% от его максимального значения?

231. На невесомом стержне длиной l = 30 см укреплены два одинаковых грузика: один - в середине стержня, другой - на одном из его концов. Стержень с грузами колеблется около горизонтальной оси, проходящей через свободный конец стержня. Определить приведенную длину L и период Т простых гармонических колебаний данного физического маятника.

232. Определить максимальное ускорение а_max материальной точки, совершающей гармонические колебания с амплитудой А = 25 см, если наибольшая скорость точки v_max= 40 см/c. Написать также уравнение колебаний.

233. Точка совершает простые гармонические колебания, уравнение которых х = А sinwt, где А = 5 см, w = 2 с^-1. В момент времени, когда точка обладала потенциальной энергией П = 0,1 мДж, на нее действовала возвращающая сила F = 5 мН. Найти этот момент времени t.

234. Определить частоту n простых гармонических колебаний диска радиусом R = 20 см около горизонтальной оси, проходящей через середину радиуса диска перпендикулярно его плоскости.

235. Определить период Т простых гармонических колебаний диска радиусом R = 40 см около горизонтальной оси, проходящей через образующую диска.

236. К спиральной пружине подвесили грузик, в результате чего пружина растянулась на x =8 см. Каков будет период колебаний грузика, если его немного поднять вверх и отпустить?

237. Материальная точка совершает простые гармонические колебания так, что в начальный момент времени смещение х₀ = 4 см, а скорость V₀ = 10 см/с. Определить амплитуду А и начальную фазу j₀ колебаний, если их период Т = 2 с.

238. К пружине подвешен груз. Максимальная кинетическая энергия колебаний груза Т _max = 1,2 Дж.Амплитуда колебаний А = 5 см. Найти коэффициент жесткости К пружины.

239. На гладком горизонтальном столе лежит шар массой M = 200 г, прикрепленный к горизонтально расположенной легкой пружине с жесткостью К = 500 Н/м. В шар попадает пуля массой m = 10 г, летящая со скоростью V = 300 м/с и застрявшая в нем. Пренебрегая сопротивлением воздуха, определить амплитуду А и период Т колебаний шара.

240. Шарик массой m = 60 г колеблется с периодом Т = 2 с. В начальный момент времени смещение шарика х₀ = 4,0 см и он обладает энергией Е = 0,02 Дж. Записать уравнение простого гармонического колебания шарика и закон изменения возрастающей силы с течением времени.

241. В опыте Юнга расстояние d между щелями равно 0,6 мм. На каком расстоянии l от щелей следует расположить экран, чтобы ширина b интерференционной полосы оказалась равной 2 мм?

242. На тонкую пленку в направлении нормали к ее поверхности падает монохроматический свет с длиной волны l = 500 нм. Отраженный от нее свет максимально усилен вследствие интерференции. Определить минимальную толщину d_min пленки, если показатель преломления материала пленки n = 1,4.

243. На стеклянную пластину положена выпуклой стороной плосковыпуклая линза. Сверху линза освещена монохроматическим светом длиной волны l = 500 нм. Найти радиус R линзы, если радиус четвертого темного кольца Ньютона в отраженном свете r₄ = 2 мм.

244. Угол α между плоскостями пропускания поляризатора и анализатора равен 30⁰. Во сколько раз изменится интенсивность света, если угол увеличить до 60⁰?

245. На тонкий стеклянный клин падает нормально параллельный пучок света с длиной волны l = 500 нм. Расстояние между соседними темными интерференционными полосами в отраженном свете в = 0,5 мм. Определить угол a между поверхностями клина. Показатель преломления стекла, из которого изготовлен клин, n = 1,6.

246. На дифракционную решетку, содержащую n = 600 штрихов на миллиметр, падает нормально белый свет. Спектр проецируется помещенной вблизи решетки линзой на экран. Определить длину l спектра первого порядка на экране, если расстояние от линзы до экрана L = 1,2 м. Границы видимого спектра l_КР = 780 нм, l_Ф = 400 нм.

247. Установка для наблюдений колец Ньютона освещаются нормально падающим монохроматическим светом (l = 590 нм). Радиус кривизны R линзы равен 5 см. Определить толщину d₃ воздушного промежутка в том месте, где в отраженном свете наблюдается третье светлое кольцо.

248. В частично поляризованном свете амплитуда светового вектора, соответствующая максимальной интенсивности света в n = 3 раза больше амплитуды, соответствующей минимальной интенсивности. Определить степень поляризации Р света.

249. На дифракционную решетку, содержащую n = 600 штрихов на миллиметр, падает нормально белый свет. Спектр проецируется помещенной вблизи решетки линзой на экран. Определить длину l спектра первого порядка на экране, если расстояние от линзы до экрана L = 1,2 м. Границы видимого спектра l_КР = 780 нм, l_Ф = 400 нм.

250. Найти показатель преломления n стекла, если при падении на него света отраженный луч будет полностью поляризован при угле преломления γ =30⁰.

251. При увеличении термодинамической температуры Т черного тела в два раза длина волны l_m, на которую приходится максимум спектральной излучательной способности, уменьшилась на Dl = 400 нм. Определить начальную Т₁ и конечную Т₂ температуры тела.

252. Красная граница фотоэффекта для цинка l₀ = 310 нм. Определить максимальную кинетическую энергию Т_max фотоэлектронов в электрон-вольтах, если на цинк падает свет с длиной волны l = 200 нм.

253. На фотоэлемент с катодом из лития падает свет с длиной волны l = 200 нм. Найти наименьшее значение задерживающей разности потенциалов U_min, которую нужно приложить к фотоэлементу, чтобы прекратить фототок. Работа выхода электронов из лития А = 2,3 эВ

254. Определить длину волны λ, массу m, и импульс р фотона с энергией ε =1,2 МэВ. Сравнить массу этого фотона с массой покоя электрона.

255. На металлическую пластину направлен пучок ультрафиолетового излучения (l = 0,25 мкм). Фототок прекращается при минимальной задерживающей разности потенциалов U_min = 0,96 В. Определить работу выхода А электронов из металла.

256. Монохроматическое излучение с длиной волны λ =550 нм падает нормально на плоскую зеркальную поверхность и давит на неё с силой F = 1,2 нН. Определить число N фотонов, ежесекундно падающих на эту поверхность.

257. Определить длину волны λ фотона, импульс которого равен импульсу электрона, обладающего скоростью v =10 Мм/с.

258. На металлическую пластинку направлен монохроматический пучок света с частотой n = 7,3×10¹⁴ Гц. Красная граница l₀ фотоэффекта для данного материала равна 560 нм. Определить максимальную скорость V_max фотоэлектронов.

259. Монохроматическое излучение с длиной волны λ = 660 нм падает нормально на плоскую зачерненную поверхность и давит на неё с силой F = 0,8 нН. Определить число N фотонов, ежесекундно падающих на эту поверхность.

260. Фотоны с энергией ε =4,8 эВ вырывают электроны из металла с работой выхода А = 4,5 эВ. Найти максимальный импульс р_max, передаваемый поверхности металла при вылете каждого электрона.

261. Протон обладает кинетической энергией Т = 1 кэВ. Определить дополнительную энергию DТ, которую необходимо ему сообщить для того, чтобы длина волны l де Бройля уменьшилась в три раза.

262. Используя соотношения неопределенностей, оценить ширину l одномерного потенциального ящика, в котором минимальная энергия электрона Е_min = 10 эВ.

263. Определить длины волн де Бройля протона, прошедшего ускоряющую разность потенциалов U = 1 кВ.

264. Электрон находится в бесконечно глубоком одномерном потенциальном ящике на втором энергетическом уровне. Какова вероятность w обнаружения электрона в крайней трети ящика?

265. Оценить с помощью соотношения неопределенностей минимальную кинетическую энергию электрона, движущегося внутри сферы радиусом R = 0,05 нм.

266. Вычислить наиболее вероятную дебройлевскую длину волны l молекул азота, содержащихся в воздухе при комнатной температуре.

267. Используя соотношения неопределенностей, оценить ширину l одномерного потенциального ящика, в котором минимальная энергия электрона Е_min = 10 эВ.

268.. В прямоугольной потенциальной яме шириной l с абсолютно непроницаемыми стенками (0 < x < l) находится частица в основном состоянии. Найти вероятность w местонахождения этой частицы в области 1/4 l < x < 3/4 l.

269. Электрон движется по окружности радиуса R = 0,8 см в однородном магнитном поле с индукцией В = 10 мТл. Определить длину волны де Бройля λ для этого электрона.

270. Оценить с помощью соотношения неопределенностей минимальную кинетическую энергию электрона, движущегося внутри сферы радиусом R = 0,05 нм.

271.. Счетчик альфа-частиц, установленный вблизи радиоактивного изотопа при первом измерении регистрировал N₁ = 1400 частиц в минуту, а через время t = 4 ч - только N₂ = 400 мин^-1. Определить период полураспада Т_1/2 изотопа.

272. Вычислить энергию ядерной реакции .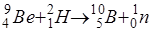

Освобождается или поглощается энергия?

273. Найти период полураспада Т_1/2 радиоактивного изотопа, если его активность за время t = 10 сут уменьшилась на 25% по сравнению с первоначальной.

274. Вычислить энергию ядерной реакции .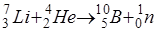

Освобождается или поглощается эта энергия?

275. Активность некоторого изотопа за время t =12 сут уменьшилась на 20%. Определить период полураспада Т_1/2 этого изотопа.

276. Вычислить энергию ядерной реакции .

Освобождается или поглощается эта энергия?

277. За один час начальное количество радиоактивного изотопа уменьшилось в 2,2 раза. Во сколько раз оно уменьшится за два часа?

278. За время t =12 суток распалось κ =2/3 начального количества ядер радиоактивного изотопа. Найти период полураспада Т_1/2 этого элемента.

279. Определить во сколько раз начальное количество ядер радиоактивного изотопа уменьшится за три года, если за один год оно уменьшилось в 4 раза.

280. Определить количество теплоты Q, выделяющейся при распаде радона активностью А = 3,7×10¹⁰ Бк за время t = 20 мин. Кинетическая энергия Т вылетающей из радона альфа-частицы равна 5,5 МэВ.

Date: 2015-11-15; view: 1130; Нарушение авторских прав