Механический смысл производной

Геометрический смысл производной

Производная в точке x 0 равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.

Рассмотрим график функции y = f (x):

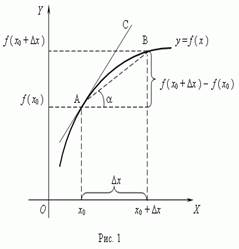Из рис.1 видно, что для любых двух точек A и B графика функции: (ф(х0+дельтаХ)-ф(х0))/дельтаХ=тгА, гдеА - угол наклона секущей AB.

Таким образом, разностное отношение равно угловому коэффициенту секущей.

Если зафиксировать точку A и двигать по направлению к ней точку B, тодельта x неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС.

Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A.

Отсюда следует: производная финкции в точке есть угловой коэф касательн к графику этой функции в этой точке

Механический смысл производной

Механический смысл производной. Рассмотрим простейший случай: движение материальной точки вдоль координатной оси, причём закон движения задан: координата x движущейся точки – известная функция x (t) времени t. В течение интервала времени от t0 до t0 + дельта t точка перемещается на расстояние: x (t0 + delta t) - x (t0) =, а её средняя скорость равна: V = delta x /delta t. При delta t стремится к 0 значение средней скорости стремится к определённой величине, которая называется мгновенной скоростью v (t0) материальной точки в момент времени t0. Но по определению производной мы имеем:

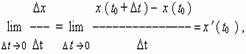отсюда, v (t0) = x’ (t0), т.e. скорость – это производная координаты по времени. В этом и состоит механический смысл производной. Аналогично, ускорение – это производная скорости по времени: a = v’ (t).

Date: 2015-10-21; view: 1088; Нарушение авторских прав