
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Продольное перемещение
|
|
Перенос груза по горизонтали вдоль судна из точки  в точку
в точку  (рис. 5.3), равносилен приложению пары сил в продольной плоскости, которая вызовет дифферент судна, в связи с чем ее момент называется дифферентующим. Величина этого момента определится выражением:
(рис. 5.3), равносилен приложению пары сил в продольной плоскости, которая вызовет дифферент судна, в связи с чем ее момент называется дифферентующим. Величина этого момента определится выражением:
 . (4.6)
. (4.6)

Рисунок 4.3 – Горизонтально-продольный перенос груза.
Аналогично предыдущему, условием равновесия будет равенство дифферентующего и продольного восстанавливающего моментов:
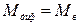 или
или  , (5.7)
, (5.7)
откуда найдется угол дифферента:
 . (5.8)
. (5.8)
При продольных наклонениях кроме угла дифферента необходимо также определить изменение осадок носом и кормой. Согласно теореме Эйлера ось равнообъемного наклонения проходит через точку  (центр тяжести площади ватерлинии), абсцисса которой
(центр тяжести площади ватерлинии), абсцисса которой  определится по диаграмме элементов теоретического чертежа. Из треугольников
определится по диаграмме элементов теоретического чертежа. Из треугольников  и
и  найдем:
найдем:
 (4.9)
(4.9)
и новые осадки носом и кормой будут:
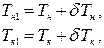 (5.10)
(5.10)
а изменение дифферента будет:
 . (5.11)
. (5.11)
Практическое занятие № 6
Тема: Влияние подвешенных и жидких грузов на остойчивость судна.
В составе нагрузки судна всегда имеются грузы, которые смещаются в сторону наклонения. Таковы, например, подвешенные и жидкие грузы.
Смещение грузов создает дополнительный момент, который изменяет угол наклонения судна от воздействия внешних моментов и поэтому рассматривается как влияющий на остойчивость судна, то есть уменьшающий его восстанавливающий момент. Рассмотрим основные виды таких грузов.
Подвешенный груз.
Если груз массой 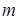 подвешен в точке
подвешен в точке  , то при наклонении судна в произвольной плоскости линия действия силы тяжести груза, оставаясь вертикальной, все время будет проходить через точку подвеса, как если бы в ней находился центр тяжести этого груза (рис. 6.1).
, то при наклонении судна в произвольной плоскости линия действия силы тяжести груза, оставаясь вертикальной, все время будет проходить через точку подвеса, как если бы в ней находился центр тяжести этого груза (рис. 6.1).

Рисунок 6.1 – Подвешенный груз.
Отсюда следует, что влияние подвешенного груза на остойчивость судна, эквивалентно перемещению груза по вертикали вверх на расстояние от его центра тяжести до точки подвеса.
Если первоначально диаграмма остойчивости рассчитана для неподвижных грузов, а затем груз массы 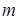 оказался подвешенным на подвесе длиной
оказался подвешенным на подвесе длиной  , то в пределах углов крена, при которых груз может свободно отклоняться, изменение диаграммы остойчивости будет таким же, как от перемещения его по вертикали в точку подвеса. При этом увеличения аппликаты центра тяжести (ЦТ) судна
, то в пределах углов крена, при которых груз может свободно отклоняться, изменение диаграммы остойчивости будет таким же, как от перемещения его по вертикали в точку подвеса. При этом увеличения аппликаты центра тяжести (ЦТ) судна  определится формулой:
определится формулой:
 , (6.1)
, (6.1)
где,
 – длина подвеса, равная:
– длина подвеса, равная:
 , (6.2)
, (6.2)
 и
и  – аппликаты центра тяжести груза и точки его подвеса, соответственно.
– аппликаты центра тяжести груза и точки его подвеса, соответственно.
Поэтому формула метацентрической высоты  , исправленной на влияние подвешенного груза, примет вид:
, исправленной на влияние подвешенного груза, примет вид:
 . (6.3)
. (6.3)
Тогда, согласно формулам (6.1), (6.2) и (6.3) получим:
 . (6.4)
. (6.4)
Когда судовой кран поднимает груз, находящийся на судне, то в момент отрыва его от палубы груз становится подвешенным и метацентрическая высота сразу изменяется до значения  , определяемого формулой (6.3). При дальнейшем его подъеме метацентрическая высота сохраняет свою величину. Если отклонение груза ограничено, то его следует считать подвешенным, лишь до угла наклонения, при котором он становится неподвижным.
, определяемого формулой (6.3). При дальнейшем его подъеме метацентрическая высота сохраняет свою величину. Если отклонение груза ограничено, то его следует считать подвешенным, лишь до угла наклонения, при котором он становится неподвижным.
Для продольной остойчивости влияние подвешенного груза выражается тем же слагаемым, что и для поперечной остойчивости (6.4). Однако в обычных условиях оно относительно мало, и им можно пренебречь.
Существенное влияние подвешенный груз имеет для плавучих кранов, у которых вес поднимаемого груза достигает 10 % от водоизмещения крана, а точка подвеса груза может находиться на большой высоте.
Жидкий груз.
В нагрузке судна всегда присутствуют подвижные грузы в виде жидкостей. Таковы, например, запасы пресной воды, топлива, смазочных масел и другие. Для наливных судов жидкие грузы составляют основную часть дедвейта. Поэтому при расчетах остойчивости всегда приходится определять влияние смещения жидких грузов.
Рассмотрим судовую цистерну, частично заполненную жидким грузом до уровня  (рис. 6.2.а).
(рис. 6.2.а).
При крене судна жидкость перетечет так, что ее свободная поверхность займет положение  параллельно новой ватерлинии
параллельно новой ватерлинии  . При этом центр тяжести жидкости сместится в сторону крена из точки
. При этом центр тяжести жидкости сместится в сторону крена из точки  в
в  . Рассматривая малые углы наклонения, кривую
. Рассматривая малые углы наклонения, кривую  можно принять за дугу окружности с центром в точке
можно принять за дугу окружности с центром в точке  , через которую в процессе наклонения все время будет проходить линия действия силы тяжести жидкости. Таким образом, в отношении остойчивости жидкий груз эквивалентен неподвижному грузу той же массы, но с центром тяжести расположенным в точке
, через которую в процессе наклонения все время будет проходить линия действия силы тяжести жидкости. Таким образом, в отношении остойчивости жидкий груз эквивалентен неподвижному грузу той же массы, но с центром тяжести расположенным в точке  , т.е. поднятому по вертикали на расстояние радиуса
, т.е. поднятому по вертикали на расстояние радиуса  .
.
Если теперь рассмотреть плавающую цистерну той же формы (рис. 6.2.б), погруженную по ватерлинию  соответственно уровню груза в цистерне, то нетрудно убедиться в том, что при наклонениях перемещения центра тяжести жидкого груза в цистерне и центра величины судна-цистерны будут тождественны, так как обе точки являются центрами тяжести одинаковых объемов.
соответственно уровню груза в цистерне, то нетрудно убедиться в том, что при наклонениях перемещения центра тяжести жидкого груза в цистерне и центра величины судна-цистерны будут тождественны, так как обе точки являются центрами тяжести одинаковых объемов.

Рисунок 6.2 – Влияние свободной поверхности жидкого груза на остойчивость судна.
Поэтому точку  можно рассматривать как метацентр
можно рассматривать как метацентр 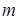 жидкого груза, а
жидкого груза, а  – как метацентрический радиус, который в соответствии с формулой (6.5) будет:
– как метацентрический радиус, который в соответствии с формулой (6.5) будет:
 ; (6.5)
; (6.5)
 , (6.6)
, (6.6)
где,
 – центральный момент инерции площади свободной поверхности жидкости в цистерне относительно оси, параллельной оси наклонения (параллельной оси
– центральный момент инерции площади свободной поверхности жидкости в цистерне относительно оси, параллельной оси наклонения (параллельной оси  );
);
 – объем жидкости в цистерне.
– объем жидкости в цистерне.
Воспользуемся опять формулой (6.4).
 .
.
Тогда для метацентрической высоты, исправленной на влияние жидкого груза, получим:
 . (6.7)
. (6.7)
Подставляя значение  и учитывая, что масса жидкости в цистерне
и учитывая, что масса жидкости в цистерне  , будем иметь:
, будем иметь:
 , (6.8)
, (6.8)
где,
 – плотность жидкости в цистерне.
– плотность жидкости в цистерне.
Из полученного выражения видно, что наличие на судне жидкого груза, имеющего свободную поверхность, уменьшает остойчивость. Поправка к метацентрической высоте не зависит от количества жидкого груза, а определяется его плотностью и моментом инерции площади свободной поверхности. Если цистерна заполнена жидкостью целиком (запрессована) так, что свободная поверхность отсутствует и  = 0, то смещения жидкости при наклонениях не будет. В этом случае остойчивость судна будет такой же, как если бы груз был твердым.
= 0, то смещения жидкости при наклонениях не будет. В этом случае остойчивость судна будет такой же, как если бы груз был твердым.
По аналогии для продольной метацентрической высоты, исправленной на влияние жидкого груза, получим:
 , (6.9)
, (6.9)
где,
 – центральный момент инерции площади свободной поверхности жидкого груза относительно оси, параллельной
– центральный момент инерции площади свободной поверхности жидкого груза относительно оси, параллельной  .
.
Для уменьшения поправки на влияние жидкого груза следует уменьшать ширину цистерн «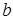 » путем разделения ее продольной переборкой (рис. 6.3).
» путем разделения ее продольной переборкой (рис. 6.3).
В первом случае в формулу (3.8) войдет величина  , равная:
, равная:
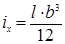 , (6.10)
, (6.10)
а при одной средней переборке суммарная величина  будет:
будет:
 , (6.11)
, (6.11)
т.е. поправка на влияние жидкого груза уменьшится в 4 раза. Нетрудно установить, что при  равномерно расставленных продольных переборках величина поправки к поперечной метацентрической высоте уменьшится в
равномерно расставленных продольных переборках величина поправки к поперечной метацентрической высоте уменьшится в  раз. Практически на современных танкерах устанавливают две продольные непроницаемые переборки, что достаточно снижает влияние жидкого груза на остойчивость.
раз. Практически на современных танкерах устанавливают две продольные непроницаемые переборки, что достаточно снижает влияние жидкого груза на остойчивость.
Как уже отмечалось выше, поправка к метацентрической высоте на влияние жидкого груза не зависит от его количества. Однако если в цистерне имеется лишь небольшой слой жидкости или если она заполнена почти полностью, то уже при малых углах крена ширина свободной поверхности резко сокращается и при дальнейшем наклонении влияние перетекания становится незначительным (рис. 6.4).

Рисунок 6.3 – Разделение цистерн продольной переборкой.

Рисунок 6.4 – Случаи недейственной потери остойчивости.
Поскольку конфигурации судовых цистерн отличаются большим разнообразием, и расчет моментов инерции их площадей для различных заполнений цистерн представляют большую сложность то для практических целей пользуются приближенными способами.
В связи с этим практически используются приближенные способы учета влияния жидких грузов на диаграмму статической остойчивости, изложенные в «Инструкции по учету влияния свободных поверхностей жидких грузов на остойчивость судна», либо способ, рекомендуемый ИМО.
Такие случаи называют недейственным влиянием жидкого груза.
Один из способов, обеспечивающих обычно запас остойчивости на больших углах крена, состоит в определении поправки для плеча статической остойчивости по формуле:
 , (6.12)
, (6.12)
где,
 – поправка для начальной метацентрической высоты;
– поправка для начальной метацентрической высоты;
 – поправочный момент к коэффициенту остойчивости;
– поправочный момент к коэффициенту остойчивости;
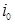 – момент инерции площади свободной поверхности жидкости при заполнении цистерны на 50 % ее емкости и отсутствии крена.
– момент инерции площади свободной поверхности жидкости при заполнении цистерны на 50 % ее емкости и отсутствии крена.
Знак суммы в выражении для  распространяется на все цистерны расчетной комбинации. В число цистерн, учитываемых при определении влияния жидкого груза на остойчивость при больших углах крена, должны включаться цистерны каждого вида жидкого груза и балласта, в которых по условиям эксплуатации могут быть одновременно свободные поверхности, причем такая их комбинация, при которой суммарный поправочный момент при крене 30º имел бы наибольшую величину при заполнении цистерн на 50 % их вместимости.
распространяется на все цистерны расчетной комбинации. В число цистерн, учитываемых при определении влияния жидкого груза на остойчивость при больших углах крена, должны включаться цистерны каждого вида жидкого груза и балласта, в которых по условиям эксплуатации могут быть одновременно свободные поверхности, причем такая их комбинация, при которой суммарный поправочный момент при крене 30º имел бы наибольшую величину при заполнении цистерн на 50 % их вместимости.
Способ исправления диаграммы остойчивости на влияние свободных поверхностей жидких грузов, рекомендованный ИМО, состоит в следующем: составляется расчетная комбинация цистерн, исходя из тех же указаний и условий, как было сказано выше, для которой определяется поправка на влияние свободной поверхности жидкого груза  для различных углов крена, причем для каждой цистерны из расчетной комбинации поправка
для различных углов крена, причем для каждой цистерны из расчетной комбинации поправка 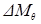 определяется по формуле:
определяется по формуле:
 , (6.13)
, (6.13)
где,  – безразмерный коэффициент, который определяется по формулам или выбирается из таблицы, в зависимости от отношения
– безразмерный коэффициент, который определяется по формулам или выбирается из таблицы, в зависимости от отношения  ;
; 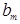 ,
,  – ширина и высота цистерны.
– ширина и высота цистерны.
Практическое занятие № 7
Тема: Диаграмма статической остойчивости, ее свойства. Плечи остойчивости формы и веса. Пантокарены, их виды. Универсальная диаграмма статической остойчивости.
Диаграмма статической остойчивости, ее свойства.
В условиях эксплуатации судна его весовое водоизмещение 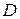 и положение центра тяжести судна
и положение центра тяжести судна 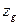 могут изменяться в широких пределах и для суждения об остойчивости судна, при различных состояниях нагрузки необходимо иметь возможность построения диаграмм статической остойчивости.
могут изменяться в широких пределах и для суждения об остойчивости судна, при различных состояниях нагрузки необходимо иметь возможность построения диаграмм статической остойчивости.
Зависимость плеча восстанавливающего момента от угла крена изображают в прямоугольных координатах, откладывая по оси абсцисс углы крена в градусах, а по оси ординат – плечи остойчивости l в метрах. Кривая, представляющая эту зависимость, называется диаграммой статической остойчивости (ДСО) или диаграммой Рида. Диаграмма статической остойчивости изображена на (рис. 7.1).

Рисунок 7.1 – Диаграмма статической остойчивости и ее параметры.
Ввиду симметрии формы судна диаграмма строится только для положительных углов крена (на правый борт). При крене на противоположный борт (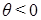 ) диаграмма продолжается как нечетная функция:
) диаграмма продолжается как нечетная функция:
 . (7.1)
. (7.1)
Характерными параметрами диаграммы являются: крутизна начального участка, максимальное плечо остойчивости  , угол максимума диаграммы
, угол максимума диаграммы 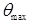 , угол заката диаграммы
, угол заката диаграммы  (при котором плечо остойчивости обращается в нуль), площадь, ограниченная кривой и осью абсцисс. Эти параметры характеризуют остойчивость на больших углах крена.
(при котором плечо остойчивости обращается в нуль), площадь, ограниченная кривой и осью абсцисс. Эти параметры характеризуют остойчивость на больших углах крена.
В зависимости от соотношений главных размерений и состояния нагрузки судна, типы диаграмм остойчивости отличаются характерными особенностями. У судов с большим отношением ширины к осадке, обладающих большой метацентрической высотой, диаграмма имеет вид выпуклой кривой, расположенной под начальной касательной на (рис. 7.2.а). Такой вид имеет диаграмма остойчивости у танкеров, балкеров и других судов, перевозящих грузы с малым удельным погрузочным объемом.




Рисунок 7.2 – Различные типы диаграмм статической остойчивости.
Для судов с высоким надводным бортом и малой начальной метацентрической высотой характерна диаграмма с точкой перегиба и начальным участком, идущим выше касательной (рис. 7.2.б). Диаграммы такого вида имеют пассажирские суда, контейнеровозы. Диаграмму первого типа называют мягкой, а второго – жесткой. Эти названия связаны с тем, что в первом случае возрастание восстанавливающего момента на начальном участке происходит медленнее, чем по линейному закону, а во втором – быстрее. Заметим, что тип диаграммы может быть разным у одного и того же судна в зависимости от величины начальной метацентрической высоты, определяемой его загрузкой.
При отрицательной начальной метацентрической высоте диаграмма имеет вид, изображенный на (рис. 7.2.в). В этом случае начальный участок диаграммы расположен под осью абсцисс, прямое положение судна неустойчиво и оно будет плавать с углом крена  , соответствующим устойчивому положению равновесия.
, соответствующим устойчивому положению равновесия.
У судов низкобортных с развитыми надстройками (некоторые типы рыболовных судов) встречаются диаграммы с двумя максимумами (двугорбые), как на (рис. 7.2.г).
Плечи остойчивости формы и веса. Пантокарены, их виды.
Для построения диаграмм статической остойчивости, при различных состояниях нагрузки судна, используют интерполяционные кривые плеч остойчивости формы или универсальные диаграммы статической остойчивости. Такие вспомогательные диаграммы рассчитываются проектирующими организациями и включаются в комплект технической документации, передаваемой на судно.
В судовых документах встречаются различные виды интерполяционных кривых, отличающихся способом разделения плеча остойчивости на составные части формы и веса, в зависимости от положения точки (полюса), от которой измеряются эти плечи.
Обычно используемые способы разделения плеча остойчивости сводятся к следующим двум случаям (рис. 7.3) и (рис. 7.4).

Рисунок 7.3 – Схема разложения плеча поперечной статической остойчивости, на плечо формы и веса.
1. При накренении судна на угол 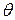 , изменяется его положение центра подводного объема судна
, изменяется его положение центра подводного объема судна  (центра величины накрененного судна), следовательно, равнодействующая сил поддержания
(центра величины накрененного судна), следовательно, равнодействующая сил поддержания  будет приложена в точке
будет приложена в точке  , а равнодействующая сил тяжести
, а равнодействующая сил тяжести  судна, приложенная в точке
судна, приложенная в точке  не изменит своего положения.
не изменит своего положения.
В качестве полюса, от которого измеряются плечи поперечной статической остойчивости до равнодействующих сил поддержания  и тяжести
и тяжести  судна, взята точка
судна, взята точка  , лежащая вначале системы координат, на пересечении основной и диаметральной плоскости судна.
, лежащая вначале системы координат, на пересечении основной и диаметральной плоскости судна.
Тогда плечо поперечной статической остойчивости представляется в виде:
 (7.2)
(7.2)
где,
 – плечо формы, измеряемое от точки
– плечо формы, измеряемое от точки  до точки
до точки  , в которую сместилась равнодействующая сил поддержания
, в которую сместилась равнодействующая сил поддержания  судна;
судна;
 – плечо веса, измеряемое от точки
– плечо веса, измеряемое от точки  до точки
до точки  , в которой приложена равнодействующая сил тяжести
, в которой приложена равнодействующая сил тяжести  судна;
судна;
 – аппликата центра тяжести судна;
– аппликата центра тяжести судна;
 – угол крена.
– угол крена.

Рисунок 7.4 – Схема разложения плеча поперечной статической остойчивости, на плечо формы и веса, с условным центром накренения судна.
2. В качестве полюса, от которого измеряются плечи поперечной статической остойчивости до равнодействующих сил поддержания  и тяжести
и тяжести  судна, взята точка
судна, взята точка  , несовпадающая с точкой
, несовпадающая с точкой  .
.
Тогда плечо поперечной статической остойчивости представляется в виде:
 (7.3)
(7.3)
где,
 – условное плечо формы, измеряемое от точки
– условное плечо формы, измеряемое от точки  до точки
до точки  , в которую сместилась равнодействующая сил поддержания
, в которую сместилась равнодействующая сил поддержания  судна;
судна;
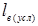 – условное плечо веса, измеряемое от точки
– условное плечо веса, измеряемое от точки  до точки
до точки  , в которой приложена равнодействующая сил тяжести
, в которой приложена равнодействующая сил тяжести  судна;
судна;
 – исправленная аппликата центра тяжести судна;
– исправленная аппликата центра тяжести судна;
 – аппликата до условного центра накренения
– аппликата до условного центра накренения  судна.
судна.
Типичный вид интерполяционных кривых, содержащих серию кривых, каждая из которых изображает зависимость плеч силы плавучести  (плеч остойчивости формы) в функции объемного водоизмещения
(плеч остойчивости формы) в функции объемного водоизмещения  и осадки судна
и осадки судна  показан на (рис. 7.5).
показан на (рис. 7.5).

Рисунок 7.5 – Пантокарены (интерполяционные кривые плеч остойчивости формы).
Все интерполяционные кривые строятся для диапазона водоизмещений от состояния судна порожнем, до состояния в полном грузу, для углов крена от 0° до 70° – 90°, обычно через равные интервалы в 10°. На каждой кривой указывается угол крена, которому она соответствует.
Интерполяционные кривые плеч остойчивости формы  могут быть представлены в табличном виде. Или в функции от объемного водоизмещения
могут быть представлены в табличном виде. Или в функции от объемного водоизмещения  судна (табл. 7.1). Или в функции от осадки
судна (табл. 7.1). Или в функции от осадки  судна (табл. 7.2).
судна (табл. 7.2).
Расчет плеч диаграммы статической остойчивости (ДСО), при использовании интерполяционных кривых, для данного объемного водоизмещения  и осадки
и осадки  судна, производится также в табличной форме (табл. 7.3).
судна, производится также в табличной форме (табл. 7.3).
Таблица 7.1 – Интерполяционные кривые плеч остойчивости формы  , в функции от объемного водоизмещения
, в функции от объемного водоизмещения  судна.
судна.
| Объемное водоизмещение, V, м3 | Плечи остойчивости формы,  , м; с аппликатой до условного центра накренения , м; с аппликатой до условного центра накренения  судна, судна,  м; при углах крена, м; при углах крена,  , град. , град.
| ||||||||
| 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | |
| 2,21 | 4,18 | 5,74 | 6,94 | 7,97 | 8,68 | 8,96 | 8,90 | 8,48 | |
| ××× | ××× | ××× | ××× | ××× | ××× | ××× | ××× | ××× | |
| ××× | ××× | ××× | ××× | ××× | ××× | ××× | ××× | ××× | |
| 1,66 | 3,34 | 5,00 | 6,29 | 7,33 | 8,04 | 8,40 | 8,50 | 8,12 |
Таблица 7.2 – Интерполяционные кривые плеч остойчивости формы  , в функции от осадки
, в функции от осадки  судна.
судна.
| Осадка, Т, м | Плечи остойчивости формы,  , м; с аппликатой до условного центра накренения , м; с аппликатой до условного центра накренения  судна, судна,  м; при углах крена, м; при углах крена,  , град. , град.
| ||||||||
| 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | |
| 4,50 | 3,21 | 5,18 | 6,74 | 7,94 | 8,97 | 9,68 | 9,96 | 9,90 | 9,48 |
| 5,00 | ××× | ××× | ××× | ××× | ××× | ××× | ××× | ××× | ××× |
| 10,00 | ××× | ××× | ××× | ××× | ××× | ××× | ××× | ××× | ××× |
| 10,50 | 2,66 | 3,34 | 6,00 | 7,29 | 8,33 | 9,04 | 9,40 | 9,50 | 9,12 |
Таблица 7.3 – Расчет плеч диаграммы статической остойчивости судна.
| Расчетные величины и формулы | Значения величин | |||||||||
Углы крена 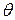 , град. , град.
| 00 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 |
Плечи остойчивости формы  , м. , м.
| снимается с пантокарен | |||||||||
Аппликата центра тяжести судна  , м. , м.
| ||||||||||
Аппликата условного центра накренения  , м. , м.
| ||||||||||
Исправленная аппликата центра тяжести судна
 , м. , м.
| ||||||||||
Плечи остойчивости веса  , м. , м.
| ||||||||||
Плечи статической остойчивости  , м. , м.
|
На оси абсцисс пантокарен (интерполяционных кривых плеч остойчивости формы), (рис. 7.5) откладывают расчетное объемное водоизмещения  или осадку
или осадку  судна и проводят вертикаль, ординаты точек, пересечения которой с кривыми определяют плечи формы
судна и проводят вертикаль, ординаты точек, пересечения которой с кривыми определяют плечи формы  , необходимые для выполнения расчета плеч диаграммы статической остойчивости в (табл. 7.3).
, необходимые для выполнения расчета плеч диаграммы статической остойчивости в (табл. 7.3).
По данным строки плеч статической остойчивости (табл. 7.3) строится диаграмма статической остойчивости (ДСО).
Универсальные диаграммы статической остойчивости.
На транспортных судах в качестве документа для построения диаграмм статической остойчивости (ДСО) получила распространение универсальная диаграмма статической остойчивости (УДСО). В отличие от интерполяционных кривых такая диаграмма позволяет определять плечи статической остойчивости для любого состояния нагрузки судна без всяких вычислений.
Универсальная диаграмма (УДСО) содержит серию кривых плеч статической остойчивости  , построенных для ряда весовых водоизмещений
, построенных для ряда весовых водоизмещений 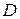 судна (обычно через равные интервалы), но для одной и той, же метацентрической высоты
судна (обычно через равные интервалы), но для одной и той, же метацентрической высоты  . Для любой другой метацентрической высоты
. Для любой другой метацентрической высоты  , исправленное плечо статической остойчивости
, исправленное плечо статической остойчивости  определяется синусоидальной поправкой.
определяется синусоидальной поправкой.
Для того чтобы избежать построения на диаграмме (УДСО) синусоидальной поправки, ось абсцисс разбивается в масштабе синусов углов крена от 0 до 1. В этом случае поправка (вычитаемое) изобразится наклонной прямой, исходящей из начала координат, а диаграммы остойчивости будут соответственно сдеформированы. Для удобства пользования диаграммой (УДСО) на оси абсцисс наносится шкала углов крена 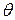 от 0° до 90°, которая будет неравномерной.
от 0° до 90°, которая будет неравномерной.
Диаграмма (УДСО) имеет две оси ординат с одинаковой ценой деления: левую, на которой нанесены значения плеча  , и правую, проходящую через точку оси абсцисс 90°, на которой нанесены значения метацентрической высоты
, и правую, проходящую через точку оси абсцисс 90°, на которой нанесены значения метацентрической высоты  .
.
Общий вид универсальной диаграммы статической остойчивости (УДСО) приведен на (рис. 7.6).
При пользовании универсальной диаграммой (УДСО), (рис.7.7) находят кривую, соответствующую расчетному весовому водоизмещению 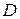 судна (если необходимо, интерполируют между соседними кривыми), а на вертикальной шкале справа находят точку
судна (если необходимо, интерполируют между соседними кривыми), а на вертикальной шкале справа находят точку  с расчетным значением
с расчетным значением  . И из начала координат проводят прямую
. И из начала координат проводят прямую  .
.
Тогда плечи статической остойчивости  изобразятся вертикальными отрезками между кривой
изобразятся вертикальными отрезками между кривой 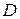 и прямой
и прямой  , измеренными в масштабе левой оси ординат. Угол заката
, измеренными в масштабе левой оси ординат. Угол заката  определится абсциссой точки пересечения кривой и прямой, а максимальное плечо
определится абсциссой точки пересечения кривой и прямой, а максимальное плечо  и угол максимума
и угол максимума  найдутся, если провести касательную к кривой
найдутся, если провести касательную к кривой 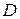 , параллельную прямой
, параллельную прямой  , как это показано на (рис. 7.7).
, как это показано на (рис. 7.7).

Рисунок 7.6 – Универсальные диаграммы статической остойчивости (УДСО).

Рисунок 7.7 – Использование универсальной диаграммы статической остойчивости (УДСО).
Практическое занятие № 8
Тема: Решение задач о статическом накренении судна по диаграмме статической остойчивости.
Основные задачи статической остойчивости.
Задачи о равновесии накрененного, статическим моментом, судна, встречающиеся в практике эксплуатации, сводятся к трем основным типам:
1. определение угла крена  при действии заданного кренящего момента
при действии заданного кренящего момента  ;
;
2. определение кренящего момента  по известному углу крена
по известному углу крена  ;
;
3. определение наибольшего кренящего момента  , который судно выдерживает не опрокидываясь.
, который судно выдерживает не опрокидываясь.
При решении будем пользоваться диаграммой статической остойчивости (ДСО), (рис. 8.1), построенной в моментах.

Рисунок 8.1 – Решение основных задач статической остойчивости.
Если диаграмма построена в плечах, то вместо кренящего момента  следует использовать кренящее плечо
следует использовать кренящее плечо  , приведенное к масштабу диаграммы делением кренящего момента на весовое водоизмещение судна:
, приведенное к масштабу диаграммы делением кренящего момента на весовое водоизмещение судна:
 . (8.1)
. (8.1)
где,
 – ускорение свободного падения, м/с2;
– ускорение свободного падения, м/с2;
 – весовое водоизмещение судна, т.
– весовое водоизмещение судна, т.
Допустим, что на судно действует внешний кренящий момент  . Положение равновесия найдется из условия равенства кренящего и восстанавливающего моментов. Для определения угла крена отложим по оси ординат диаграммы отрезок
. Положение равновесия найдется из условия равенства кренящего и восстанавливающего моментов. Для определения угла крена отложим по оси ординат диаграммы отрезок  , равный, в масштабе моментов, величине
, равный, в масштабе моментов, величине  и проведем горизонталь
и проведем горизонталь  до пересечения с диаграммой на (рис. 8.1).
до пересечения с диаграммой на (рис. 8.1).
Тогда угол  и будет искомым углом крена судна.
и будет искомым углом крена судна.
Обратная задача – определение действующего кренящего момента по углу крена судна для случая постоянного момента решается обратным построением. По оси абсцисс откладываем известный угол крена, проводим вертикаль до пересечения с диаграммой и через полученную точку – горизонталь до оси ординат, по которой прочитываем значение действующего момента. Если при отложенном угле крена диаграмма пересекается с осью абсцисс, то крен судна является следствием отрицательной начальной остойчивости, а не воздействия внешнего кренящего момента.
Третья задача – определение наибольшего выдерживаемого судном кренящего момента  решается измерением в масштабе по шкале моментов наибольшей ординаты диаграммы статической остойчивости. Если диаграмма построена в плечах остойчивости, то наибольший момент найдется по формуле
решается измерением в масштабе по шкале моментов наибольшей ординаты диаграммы статической остойчивости. Если диаграмма построена в плечах остойчивости, то наибольший момент найдется по формуле  , где
, где 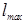 – наибольшая ордината диаграммы. Абсцисса максимума диаграммы
– наибольшая ордината диаграммы. Абсцисса максимума диаграммы  определит наибольший угол крена, до которого судно может быть наклонено постоянным моментом, не опрокидывая его.
определит наибольший угол крена, до которого судно может быть наклонено постоянным моментом, не опрокидывая его.
Практическое занятие № 9
Тема: Понятие о динамической остойчивости судна. Диаграмма динамической остойчивости, ее свойства. Расчет плеч динамической остойчивости.
Понятие о динамической остойчивости судна.
Внешние моменты, действующие на судно, различаются по характеру их приложения к судну.
Перекачка жидкого груза между цистернами, расположенными на разных бортах, прием жидкого груза на один борт представляют случаи, когда кренящий момент  возрастает настолько медленно, что скорость накренения судна практически незаметна. В таких случаях можно считать, что в каждый момент времени, восстанавливающий момент
возрастает настолько медленно, что скорость накренения судна практически незаметна. В таких случаях можно считать, что в каждый момент времени, восстанавливающий момент  уравновешивает кренящий
уравновешивает кренящий  и судно все время находится в равновесии. Такие кренящие моменты считаются приложенными статически.
и судно все время находится в равновесии. Такие кренящие моменты считаются приложенными статически.
Противоположным по характеру приложения является кренящий момент от действия шквала. Измерения скорости и давления ветра показывают, что при сильных шквалах нарастание давления до полной величины может происходить за единицы и даже доли секунды. За такое время судно не успевает отклониться на сколько-нибудь значительный угол и можно считать, что кренящий момент прикладывается к судну внезапно. Кренящий момент такого характера называется динамическим кренящим моментом, а противодействие судна такому моменту – динамической остойчивостью.
В этом случае, состояние равновесия судна при накренении на динамический угол крена  , если кренящий момент будет равен восстанавливающему моменту
, если кренящий момент будет равен восстанавливающему моменту  , не наступит. Только когда работа кренящего момента станет равной работе восстанавливающего момента
, не наступит. Только когда работа кренящего момента станет равной работе восстанавливающего момента  , накренение прекратится и для судна наступит условие равновесия.
, накренение прекратится и для судна наступит условие равновесия.
Таким образом, мерой динамической остойчивости судна является работа восстанавливающего момента  .
.
Диаграмма динамической остойчивости, ее свойства. Расчет плеч динамической остойчивости.
Диаграмма, изображающая зависимость работы восстанавливающего момента  от угла крена
от угла крена  , называется диаграммой динамической остойчивости (ДДО), (рис. 9.1).
, называется диаграммой динамической остойчивости (ДДО), (рис. 9.1).
Работа восстанавливающего момента от угла крена определяется формулой:
 . (9.1)
. (9.1)
Из формулы (9.1) ясно, что диаграмма динамической остойчивости (ДДО) есть интегральная кривая по отношению к диаграмме статической остойчивости (ДСО), которая является первообразной кривой.
Из сказанного следуют, что диаграмма динамической остойчивости (ДДО) обладает такими свойствами:
1. ордината диаграммы динамической остойчивости при угле крена 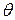 , с учетом масштаба, равна площади диаграммы статической остойчивости до этого же угла крена
, с учетом масштаба, равна площади диаграммы статической остойчивости до этого же угла крена 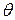 ;
;
2. в начале координат и при угле заката  диаграмма динамической остойчивости (ДДО) имеет соответственно минимум и максимум (устойчивое и неустойчивое положения равновесия судна);
диаграмма динамической остойчивости (ДДО) имеет соответственно минимум и максимум (устойчивое и неустойчивое положения равновесия судна);
3. углу максимума диаграммы статической остойчивости соответствует точка перегиба диаграммы динамической остойчивости;
4. диаграмма динамической остойчивости (ДДО) есть четная функция угла крена 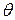 , и является кривой, симметричной относительно оси ординат. При крене на противоположный борт (
, и является кривой, симметричной относительно оси ординат. При крене на противоположный борт (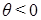 ) диаграмма продолжается как нечетная функция:
) диаграмма продолжается как нечетная функция:  .
.

Рисунок 9.1 – Диаграмма динамической остойчивости (ДДО).
Если восстанавливающий момент представить в виде  , то из формулы (9.1) следует:
, то из формулы (9.1) следует:

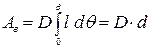 , (9.2)
, (9.2)
где,
 – плечо динамической остойчивости.
– плечо динамической остойчивости.
Для его определения из работы восстанавливающего момента, также можно использовать формулу:

 , (9.3)
, (9.3)
где,
 – ускорение свободного падения, м/с2;
– ускорение свободного падения, м/с2;
 – весовое водоизмещение судна, т.
– весовое водоизмещение судна, т.
Расчет плеч диаграммы динамической остойчивости (ДДО) выполняется интегрированием плеч диаграммы статической остойчивости (ДСО) в табличной форме (табл. 9.1).
Таблица 9.1 – Расчет плеч диаграммы динамической остойчивости судна.
| Расчетные величины и формулы | Значения величин | |||||||||
Углы крена 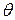 , град. , град.
| 00 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 |
Плечи статической остойчивости 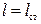 , м. , м.
| ||||||||||
Интегральные суммы  , м. , м.
| ||||||||||
Плечи динамической остойчивости
 ,м × рад. ,м × рад.
|
Интегральные суммы вычисляются методом трапеции по формуле:
 , (9.4)
, (9.4)
где, индекс  означает предыдущую колонку (табл. 9.1).
означает предыдущую колонку (табл. 9.1).
Это означает, что для вычисления интегральных сумм плеч динамической остойчивости используются формулы:
При угле крена  –
– 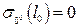 ;
;
При угле крена  –
–  ;
;
При угле крена  –
–  ;
;
При угле крена  –
–  ;
;
При угле крена  –
–  ;
;
При угле крена  –
–  ;
;
При угле крена  –
– 
 ;
;
При угле крена  –
– 
 ;
;
При угле крена  –
– 
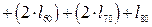 ;
;
При угле крена  –
– 
 .
.
При вычислении плеч динамической остойчивости в (табл. 9.1), шаг углов крена берется в радианной мере  рад. Приведенный в (табл. 9.1), способ расчета плеч динамической остойчивости пригоден только для постоянного шага на всем интервале углов крена
рад. Приведенный в (табл. 9.1), способ расчета плеч динамической остойчивости пригоден только для постоянного шага на всем интервале углов крена 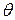 .
.
По данным строки плеч динамической остойчивости (табл. 9.1), строится в виде плавной кривой диаграмма динамической остойчивости (ДДО).
Практическое занятие № 10
Тема: Решение задач о динамическом накренении судна по диаграммам статической и динамической остойчивости.
Основные задачи динамической остойчивости.
Допустим, что на судно динамически подействовал кренящий момент 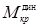 , который будем считать постоянным. Его график на диаграмме статической остойчивости (ДСО) изобразится горизонтальной прямой
, который будем считать постоянным. Его график на диаграмме статической остойчивости (ДСО) изобразится горизонтальной прямой  (рис. 10.1).
(рис. 10.1).

Рисунок 10.1 – Определение динамического угла крена.
На участке наклонения от  до
до  кренящий момент больше восстанавливающего и судно будет крениться с возрастающей угловой скоростью. В точке
кренящий момент больше восстанавливающего и судно будет крениться с возрастающей угловой скоростью. В точке  кренящий и восстанавливающий моменты уравновесятся, но судно придет в нее, имея некоторую угловую скорость, поэтому оно будет продолжать крениться. Восстанавливающий момент становится больше кренящего и угловая скорость будет убывать, пока не обратится в нуль при некотором угле крена
кренящий и восстанавливающий моменты уравновесятся, но судно придет в нее, имея некоторую угловую скорость, поэтому оно будет продолжать крениться. Восстанавливающий момент становится больше кренящего и угловая скорость будет убывать, пока не обратится в нуль при некотором угле крена  , после чего судно начнет возвращаться к положению равновесия
, после чего судно начнет возвращаться к положению равновесия  , перейдет его и, таким образом, будет совершать колебания около положения равновесия, пока они не затухнут благодаря силам сопротивления и судно не остановится при угле равновесия
, перейдет его и, таким образом, будет совершать колебания около положения равновесия, пока они не затухнут благодаря силам сопротивления и судно не остановится при угле равновесия  .
.
Практический интерес представляет угол наклонения судна, от динамически приложенного кренящего момента  , который называется динамическим углом крена
, который называется динамическим углом крена  . Очевидно, что судно при наклонении достигнет такого угла крена
. Очевидно, что судно при наклонении достигнет такого угла крена  , при котором оно полностью израсходует кинетическую энергию вращения, приобретенную за счет работы динамического кренящего момента.
, при котором оно полностью израсходует кинетическую энергию вращения, приобретенную за счет работы динамического кренящего момента.
Условием определения динамического угла крена является равенство работ кренящего и восстанавливающего моментов, т.е. равенство площадей  и
и  . Так как трапеция
. Так как трапеция  есть общая часть обеих указанных площадей, то их равенство эквивалентно равенству площадей
есть общая часть обеих указанных площадей, то их равенство эквивалентно равенству площадей  и
и  , изображающих соответственно работу избытка кренящего момента и работу избытка восстанавливающего момента. Из сказанного следует, что определение динамического угла крена, вызванного динамическим моментом заданной величины, сводится к нахождению положения вертикали
, изображающих соответственно работу избытка кренящего момента и работу избытка восстанавливающего момента. Из сказанного следует, что определение динамического угла крена, вызванного динамическим моментом заданной величины, сводится к нахождению положения вертикали  , ограничивающей равные по величине площади, заштрихованные на (рис. 10.1).
, ограничивающей равные по величине площади, заштрихованные на (рис. 10.1).
Вторая задача динамической остойчивости состоит в определении величины динамического кренящего момента, вызвавшего наклонение судна на угол  . Решается она построением вертикальной прямой
. Решается она построением вертикальной прямой  , определяющей
, определяющей  на (рис. 10.1), и подбором горизонтальной прямой
на (рис. 10.1), и подбором горизонтальной прямой  , выполняющей условие равенства заштрихованных площадей
, выполняющей условие равенства заштрихованных площадей  и
и  . Ордината этой прямой соответствует величине искомого кренящего момента
. Ордината этой прямой соответствует величине искомого кренящего момента  .
.
Третья задача динамической остойчивости заключается в нахождении наибольшего динамически приложенного кренящего момента, называемого опрокидывающим  , который судно может выдержать не опрокидываясь. Отыскание этого момента сводится к определению такой горизонтали
, который судно может выдержать не опрокидываясь. Отыскание этого момента сводится к определению такой горизонтали  , которая ограничивает площадь сегмента
, которая ограничивает площадь сегмента  , равную площади
, равную площади  (на рис. 10.2. заштрихованы).
(на рис. 10.2. заштрихованы).

Рисунок 10.2 – Определение наибольшего динамически приложенного момента  , выдерживаемого судном.
, выдерживаемого судном.
При этом определяется и предельный динамический угол крена  , на который судно может быть наклонено динамическим моментом
, на который судно может быть наклонено динамическим моментом  .
.
Теперь рассмотрим решение задач по определению динамического угла крена  при действии заданного кренящего момента
при действии заданного кренящего момента  и определению наибольшего динамического момента
и определению наибольшего динамического момента  , выдерживаемого судном по диаграмме динамической остойчивости (ДДО), (рис. 10.3).
, выдерживаемого судном по диаграмме динамической остойчивости (ДДО), (рис. 10.3).

Рисунок 10.3 – Решение основных задач по диаграмме динамической остойчивости (ДДО).
Допустим, что на судно динамически подействовал кренящий момент постоянной величины  . Приравняв работу кренящего момента к работе восстанавливающего момента
. Приравняв работу кренящего момента к работе восстанавливающего момента  , из формулы (9.1) получим линейную зависимость
, из формулы (9.1) получим линейную зависимость  , которая изображается прямой, исходящей из начала координат.
, которая изображается прямой, исходящей из начала координат.
Если диаграмма динамической остойчивости (ДДО) построена в масштабе плеч, тогда используем формулу (9.3) 
где,
 – ускорение свободного падения, м/с2;
– ускорение свободного падения, м/с2;
 – весовое водоизмещение судна, т.
– весовое водоизмещение судна, т.
Для построения линейной зависимости на оси абсцисс откладываем угол  рад., и по вертикали откладываем отрезок, равный ординате работе
рад., и по вертикали откладываем отрезок, равный ординате работе  . Которая при этом угле численно равна кренящему моменту
. Которая при этом угле численно равна кренящему моменту  .
.
Это прямая, проходящая через начало координат и верхний конец отрезка  , изображает искомую зависимость работы
, изображает искомую зависимость работы  кренящего момента от угла
кренящего момента от угла 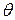 . Точка пересечения этой прямой с диаграммой динамической остойчивости (ДДО) определяет динамический угол крена
. Точка пересечения этой прямой с диаграммой динамической остойчивости (ДДО) определяет динамический угол крена  как угол, соответствующий равенству работ кренящего и восстанавливающего моментов
как угол, соответствующий равенству работ кренящего и восстанавливающего моментов  (рис. 10.3).
(рис. 10.3).
Для определения наибольшего динамического момента  , который выдержит судно не опрокидываясь, проводим касательную к диаграмме динамической остойчивости (ДДО). На оси абсцисс откладываем угол
, который выдержит судно не опрокидываясь, проводим касательную к диаграмме динамической остойчивости (ДДО). На оси абсцисс откладываем угол  рад., и по вертикали откладываем отрезок, равный ординате работе наибольшего динамического момента
рад., и по вертикали откладываем отрезок, равный ординате работе наибольшего динамического момента  .
.
Точка пересечения этой касательной с диаграммой динамической остойчивости (ДДО) определяет предельный динамический угол крена  , соответствующий равенству работ наибольшего динамического и восстанавливающего моментов
, соответствующий равенству работ наибольшего динамического и восстанавливающего моментов  (рис. 10.3).
(рис. 10.3).
Практическое занятие № 11
Тема: Силы, действующие на корпус судна. Общая и местная прочность корпуса. Расчет изгибающих моментов и перерезывающих сил. Прочность на тихой воде и на волнении.<
Date: 2015-10-19; view: 845; Нарушение авторских прав