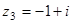Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Задание 7. Найти значение производной функции в точке, если
|
|
Контрольная работа 5
Задание 1. Найти модули и главные аргументы чисел и изобразить числа в комплексной плоскости:
1) 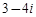 2)
2)  3)
3)  4)
4) 
| 1)  2)
2) 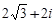 3)
3)  4)
4) 
| ||
1)  2)
2)  3)
3)  4)
4) 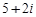
| 1)  2)
2)  3)
3)  4)
4) 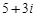
| ||
1)  2)
2) 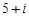 3)
3)  4)
4) 
| 1)  2)
2)  3)
3)  4)
4) 
| ||
1)  2)
2)  3)
3)  4)
4) 
| 1)  2)
2)  3)
3)  4)
4) 
| ||
1)  2)
2)  3)
3)  4)
4) 
| 1)  2)
2)  3)
3)  4)
4) 
|
Задание 2. Найти мнимую и вещественную часть комплексных чисел:
1)  2)
2)  3)
3)  4)
4) 
| 1)  2)
2)  3)
3)  4)
4) 
| ||
1)  2)
2)  3)
3)  4)
4) 
| 1)  2)
2)  3)
3) 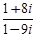 4)
4) 
| ||
1)  2)
2)  3)
3)  4)
4) 
| 1)  2)
2)  3)
3)  4)
4) 
| ||
1)  2)
2)  3)
3)  4)
4) 
| 1) 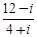 2)
2)  3)
3)  4)
4) 
| ||
1)  2)
2)  3)
3)  4)
4) 
| 1)  2)
2)  3)
3)  4)
4) 
|
Задание 3. Записать комплексные числа в тригонометрической и показательной форме:
1)  2)
2)  3)
3)  4)
4) 
| 1)  2)
2)  3)
3)  4)
4) 
| ||
1)  2)
2)  3)
3)  4)
4) 
| 1)  2)
2)  3)
3)  4)
4) 
| ||
1)  2)
2)  3)
3)  4)
4) 
| 1)  2)
2)  3)
3)  4)
4) 
| ||
1)  2)
2)  3)
3)  4)
4) 
| 1)  2)
2)  3)
3)  4)
4) 
| ||
1)  2)
2)  3)
3)  4)
4) 
| 1)  2)
2)  3)
3)  4)
4) 
|
Задание 4. Даны два комплексных числа. Найти действительную часть числа, если
 , , 
|  , , 
| ||
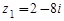 , , 
|  , , 
| ||
 , , 
|  , , 
| ||
 , , 
|  , , 
| ||
 , , 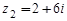
| 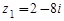 , , 
|
Задание 5. Дано комплексное число. Выполнить операции,,,, если

| 
| ||

| 
| ||

| 
| ||

| 
| ||

| 
|
Задание 6. Найти значение функций комплексного переменного,,, в точке

| 
| ||
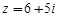
| 
| ||
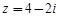
| 
| ||

| 
| ||

| 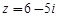
|
Задание 7. Найти значение производной функции в точке, если
 , , 
|  , , 
| ||
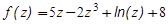 , , 
|  , , 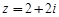
| ||
 , , 
|  , , 
| ||
 , , 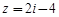
|  , , 
| ||
 , , 
|  , , 
|
Примечание: вариант определяется по последней цифре зачетки!!
Образец индивидуального задания по комплексным числам.
Задание 1. Найдите модули и главные аргументы чисел и изобразите числа в комплексной плоскости:
1) 
2) 
3) 
4) 
Задание 2. Найдите мнимую и вещественную часть комплексных чисел:
1) 
| 2) 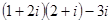
| 3) 
| 4) 
|
Задание 3. Запишите комплексные числа в тригонометрической и показательной форме:
1) 
| 2) 
| 3) 
| 4) 
|
Задание 4. Даны два комплексных числа  ,
,  . Тогда действительная часть числа
. Тогда действительная часть числа  равна …
равна …
Задание 5. Дано комплексное число 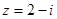 . Выполнить операции:
. Выполнить операции:
1) 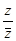
| 2) 
| 3) 
| 4) 
|
Задание 6. Найдите значение функции комплексного переменного в точке
:
1) 
| 2) 
| 3) 
| 4) 
|
Задание 7. Если  , то значение производной этой функции в точке
, то значение производной этой функции в точке  равно …
равно …
Решение задачи 1)
Будем использовать материал лекции (2) (см., в частности, определения 6 и 7 и формулы (1), (2) и (3)).
1) 

Найдем главное значение аргумента из равенства: Тогда 2)

Имеем, Найдем главное значение аргумента, пользуясь равенством Тогда Очевидно, угол Если 3) |
|
 .
.
 .
.
Тогда  , где
, где  .
.
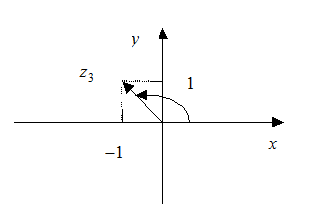
Из рисунка 22 видно, что  угол II четверти. При
угол II четверти. При 
 .
.
4) 
|

 Имеем,
Имеем,  .
.
 .
.
Тогда  , где
, где  . Из рисунка 23 видно, что
. Из рисунка 23 видно, что  угол III четверти. Если
угол III четверти. Если  , то
, то  .
.
Решение задачи 2).
Воспользуемся определением 1 из лекции 1.
1) 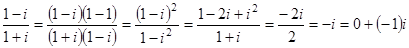
 ;
;  .
.
2) 
 ;
;  .
.
3) 
 ;
; 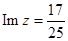 .
.
4) 


 ;
; 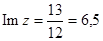 .
.
Решение задачи 3)
1) 
Решение этой задачи опирается на решение примера 4 из лекции 2.
|
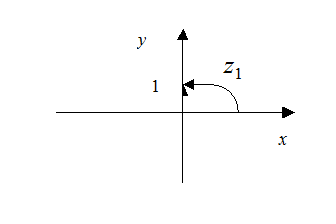
 Имеем,
Имеем,  . Из рисунка 24 видно, что угол
. Из рисунка 24 видно, что угол  равен
равен  .
.
Тригонометрическая форма комплексного числа имеет вид

Воспользуемся определением 10 и соотношением (13) из лекции 4. Получим показательную форму комплексного числа

2) 
|


Имеем,  .
.
 .
.
Тогда 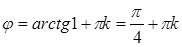 , где
, где  . Из рисунка 25 видно, что
. Из рисунка 25 видно, что  угол I четверти. Если
угол I четверти. Если  , то
, то  .
.


3) 
|

 Имеем,
Имеем,  .
.
 .
.
Тогда  , где
, где  .
.
Угол  располагается во II четверти.
располагается во II четверти.
При 
 .
.
 .
.
 .
.
4) 
|

 Имеем,
Имеем,  .
.
Из рисунка видно, что угол  равен
равен  . Тогда
. Тогда 
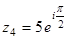
Решение задачи 4)
Воспользуемся материалом лекции 1.






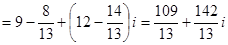 .
.
Тогда 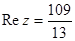 .
.
Решение задачи 5)
1) 

2) 
3) 
4) 
 .
.
Решение задачи 6)
1) 
2) 
3) 

4) 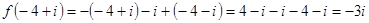
Решение задачи 7)

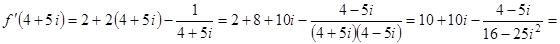

Date: 2015-10-19; view: 449; Нарушение авторских прав
 .
. .
.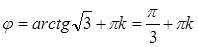 , где
, где  .
.

 .
.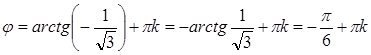 , где
, где  .
.