
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Измерение скорости звука
|
|
Грубое измерение скорости звука в воздухе может произвести каждый.
Путешествуя в горах, катаясь на лодке по тихой реке, окаймленной крутыми или лесистыми берегами, находясь перед опушкой густого леса, легко воспроизвести знакомое всем явление эхо. Подобно тому как волны на воде, встречая на пути препятствие, отражаются от него, так и звук отражается от преграды. Если звуковые волны падают на преграду под прямым углом, отраженные волны распространяются точно в обратном направлении.
Явление эхо, или отражение звука от препятствия на пути распространения звуковых волн, позволяют сравнительно простым способом измерять скорость звука. Для такого измерения нужно иметь часы с секундной стрелкой или, лучше, секундомер. Замечая момент посылки звука (крик, хлопанье в ладоши, стук) и момент приема эха, можно определить скорость звука с, если известно расстояние L до отражающей поверхности (леса или берега). Скорость звука с определится из формулы
 ,
,
где t – измеренный промежуток времени. По этой формуле число 2 стоит потому, что звук дважды проходит расстояние L. При помощи этой формулы можно определить расстояние L до препятствия, зная скорость звука с и промежуток времени t. На этом принципе, как мы увидим дальше, основаны измерения глубины морей и рек при помощи так называемых эхолотов.
Можно также произнести измерение скорости звука воспользовавшись тем обстоятельством, что скорость распространения света неизмеримо больше скорости звука (примерно в миллион раз). Мы видим клубок белого пара и уже потом слышим свисток приближающегося паровоза; видим молнию и только через некоторое время слышим раскат грома. Скорость света равна 300 000 км/сек; в настоящее время в природе не обнаружено скорости переноса энергии большей, чем эта скорость.
Если на расстоянии L, от места наблюдения создать звук одновременно со вспышкой света (например, взрыв, выстрел) и измерить промежуток времени между световой вспышкой и приходом звукового сигнала в точку наблюдения, то скорость звука будет равна:
 .
.
При таком измерении мы пренебрегаем временем распространения света от источника звука до места его приема. Но это время столь ничтожно, что пренебрежение им практически не вносит никакой ошибки в результат измерения.
Имеется много других более точных способов измерения скорости звука в воздухе; с некоторыми из них мы познакомимся в дальнейшем. Скорость звука при температуре 0°С оказывается равной 331,5 м/сек, или около 1200 км/час.
Чтобы нагляднее представить себе величину этой скорости, укажем, что скорость современных реактивных самолетов близка к скорости звука (например, пассажирский самолет ТУ-104 может развить скорость около 1000 км/час) и может быть даже больше ее. Скорость полета снарядов противотанковой и зенитной артиллерии — 1000 и более м/сек, т.е. в несколько раз больше скорости звука; скорость полета ракеты при выводе спутника на орбиту несколько более 8 км/ceк.
От чего зависит скорость звука. Чем же определяется значение скорости звука в воздухе? Можно показать, что скорость распространения продольной волны в упругой среде выражается формулой
 ,
,
где Е — так называемый модуль объемной упругости, или величина, обратная сжимаемости среды, и 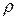 — плотность среды. Смысл величины Е мы можем уяснить на следующем примере.
— плотность среды. Смысл величины Е мы можем уяснить на следующем примере.
Нажмем на ручку велосипедного насоса, закрыв выходное отверстие резинового шланга. Если первоначальный объем воздуха под поршнем был V0, и давление р0, то после сжатия до давления р этот объем уменьшится и станет равным V. Изменение объема равно V0 — V, а его относительное изменение 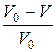 . Чем больше сила
. Чем больше сила  , которая сжимает воздух (или какой-либо другой газ), тем больше будет относительное изменение объема; именно, относительное изменение объема газа прямо пропорционально приложенной силе:
, которая сжимает воздух (или какой-либо другой газ), тем больше будет относительное изменение объема; именно, относительное изменение объема газа прямо пропорционально приложенной силе:
 .
.
В этой формуле k — некоторая постоянная величина, называемая сжимаемостью газа; чем меньше относительное изменение объема при заданной силе F, тем меньше сжимаемость газа. Из этой формулы следует, что сжимаемость равна относительному изменению объема при изменении давления на единицу. Величина  , обратная сжимаемости, называется модулем, или коэффициентом объемной упругости среды, или просто объемной упругостью.
, обратная сжимаемости, называется модулем, или коэффициентом объемной упругости среды, или просто объемной упругостью.
Итак, упругость есть сила, противодействующая сжатию воздуха. Внешнее давление, под которым воздух находится, сближает частицы воздуха, сила же упругости стремится его расширить. При равенстве этих сил воздух находится в равновесии. Внешнее давление, таким образом, служит мерой упругости, и упругость воздуха, как и других газов, численно равна абсолютной величине давления, которое газ оказывает на единицу поверхности, т. е. на 1 см2. Формулу для скорости звука можно поэтому записать в виде

В этой формуле Р — давление на уровне моря при 0°С. Оно равно 1033,6 Г/см2 и должно быть представлено в абсолютных единицах. Вспомним, что в механике за единицу силы принимают силу, сообщающую массе в 1 г ускорение в 1 см/сек2. Эта единица силы называется диной. Так как по закону Ньютона сила равна массе, умноженной на ускорение, а ускорение силы тяжести равно 980,6 см/сек2, то сила, с которой земля притягивает 1 г, равна 980,6 абс. единиц. Таким образом, атмосферное давление Р, выраженное в абсолютных единицах, будет равно 1033,6×980,6 = 1013500 абс. единиц. Абсолютная единица давления называется б а р о м. Бар — это давление силы в 1 дину на 1 см2.
Что касается плотности воздуха 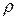 , то при температуре 0°С и нормальном атмосферном давлении эта плотность, т. е. масса 1 см3, выраженная в граммах, равна 0,001293. Если подставить эти значения для Р и
, то при температуре 0°С и нормальном атмосферном давлении эта плотность, т. е. масса 1 см3, выраженная в граммах, равна 0,001293. Если подставить эти значения для Р и 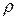 в последнюю формулу, то окажется, что скорость звука равна 280 м/сек. Такое значение для с теоретически впервые получил Ньютон. Эта величина намного отличается от той скорости, с которой действительно распространяется звук в воздухе, равной, как мы уже указывали, 331,5 м/сек при 0°С.
в последнюю формулу, то окажется, что скорость звука равна 280 м/сек. Такое значение для с теоретически впервые получил Ньютон. Эта величина намного отличается от той скорости, с которой действительно распространяется звук в воздухе, равной, как мы уже указывали, 331,5 м/сек при 0°С.
Дело в том, что в нашем рассуждении при обосновании этой формулы мы не учитывали одного обстоятельства. При сжатии воздуха увеличивается давление и, следовательно, растет упругость воздуха. Но, кроме этого, воздух, как и всякий газ, при сжатии нагревается, а при разрежении охлаждается. Изменение температуры воздуха приводит к добавочному изменению его упругости; при сжатии за счет повышения температуры упругость несколько возрастает, при разрежении — несколько уменьшается.
Добавочное изменение упругости воздуха при сжатии может, конечно, получиться только в том случае, если сжатие происходит так, что выделившееся тепло не успевает уйти. Точно так же, если быстро произвести разрежение, получившаяся разность в температуре не успеет выровняться. Такой процесс, при котором не происходит обмена теплом с окружающей средой, называется адиабатическим процессом. Когда происходит выравнивание температуры (т.е. когда температура постоянна), процесс называется изотермическим.
В предыдущем рассуждении мы принимали во внимание только изменение упругости за счет сжатий и разрежений воздуха, но упустили из виду, что эти сжатия и разрежения сопровождаются изменениями температуры. Изменения же температуры, как мы видим, приводят к добавочному изменению упругости воздуха. На это обстоятельство впервые указал Лаплас.
Лаплас показал, что отношение величины упругости при адиабатическом сжатии к величине упругости при медленном сжатии, когда температура сжатого воздуха успевает выровняться с температурой окружающей среды, равно отношению количеств тепла, необходимых для нагревания единицы массы воздуха на 1°С при постоянном давлении и при постоянном объеме. Это отношение называется отношением теплоемкостей при постоянном давлении ср и при постоянном объеме  . Для воздуха
. Для воздуха  .Если мы учтем эти добавочные изменения упругости воздуха, то формула для скорости звука запишется в виде:
.Если мы учтем эти добавочные изменения упругости воздуха, то формула для скорости звука запишется в виде:
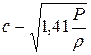 .
.
Легко проверить вычислением, что из этой формулы для с получается в точности то значение скорости звука, которое дает эксперимент, т.е. 331,5 м/сек (при 0°С).
Таким образом, скорость звука увеличивается благодаря изменениям в температуре, производимым самой звуковой волной, и процесс распространения звука есть процесс адиабатический. Эти изменения температуры очень малы; они не влияют на среднюю температуру воздуха, так как в сгущениях температура несколько возрастает, но зато в разрежениях понижается.
Date: 2015-10-18; view: 539; Нарушение авторских прав