
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Нормативные и расчетные значения характеристик бетона
|
|
Нормативные значения прочностных характеристик бетона
5.1.8 Основными прочностными характеристиками бетона являются нормативные значения:
- сопротивления бетона осевому сжатию Rb,n;
- сопротивления бетона осевому растяжению Rbt,n.
Нормативные значения сопротивления бетона осевому сжатию (призменная прочность) и осевому растяжению (при назначении класса бетона по прочности на сжатие) принимают в зависимости от класса бетона по прочности на сжатие В согласно таблице 5.1.
При назначении класса бетона по прочности на осевое растяжение В t, нормативные значения сопротивления бетона осевому растяжению Rbt,n принимают равными числовой характеристике класса бетона на осевое растяжение.
Расчетные значения прочностных характеристик бетона
5.1.9 Расчетные значения сопротивления бетона осевому сжатию Rb и осевому растяжению Rbt, определяют по формулам:
 ; ;
| (5.1) |
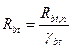 ; ;
| (5.2) |
Значения коэффициента надежности по бетону при сжатии γb принимают равными:
1,3 - для предельных состояний по несущей способности (первая группа);
1,0 - для предельных состояний по эксплуатационной пригодности (вторая группа).
Значения коэффициента надежности по бетону при растяжении γbt принимают равными:
1,5 - для предельных состояний по несущей способности при назначении класса бетона по прочности на сжатие;
1,3 - для предельных состояний по несущей способности при назначении класса бетона по прочности на осевое растяжение;
1,0 - для предельных состояний по эксплуатационной пригодности.
Расчетные значения сопротивления бетона Rb, Rbt, Rb,ser, Rbt,ser (c округлением) в зависимости от класса бетона по прочности на сжатие и осевое растяжение приведены: для предельных состояний первой группы - соответственно в таблицах 5.2 и 5.3, второй группы - в таблице 5.1.
Таблица 5.1
| Вид сопротивления | Нормативные значения сопротивления бетона Rb,n и Rbt,n и расчетные значения сопротивления бетона для предельных состояний второй группы Rb,ser и Rbt,ser, МПа, при классе бетона по прочности на сжатие | ||||||||||
| B10 | B15 | В20 | В25 | B30 | В35 | В40 | В45 | В50 | В55 | В60 | |
| Сжатие осевое (призменная прочность) Rb,n, Rb,ser | 7,5 | 11,0 | 15,0 | 18,5 | 22,0 | 25,5 | 29,0 | 32,0 | 36,0 | 39,5 | 43,0 |
| Растяжение осевое Rbt,n, Rbt,ser | 0,85 | 1,1 | 1,35 | 1,55 | 1,75 | 1,95 | 2,1 | 2,25 | 2,45 | 2,6 | 2,75 |
Таблица 5.2
| Вид сопротивления | Расчетные значения сопротивления бетона для предельных состояний первой группы Rb и Rbt МПа, при классе бетона по прочности на сжатие | ||||||||||
| B10 | B15 | В20 | В25 | B30 | В35 | В40 | В45 | В50 | В55 | В60 | |
| Сжатие осевое (призменная прочность) Rb | 6,0 | 8,5 | 11,5 | 14,5 | 17,0 | 19,5 | 22,0 | 25,0 | 27,5 | 30,0 | 33,0 |
| Растяжение осевое Rbt | 0,56 | 0,75 | 0,9 | 1,05 | 1,15 | 1,3 | 1,4 | 1,5 | 1,6 | 1,7 | 1,8 |
Таблица 5.3
| Вид сопротивления | Расчетные значения сопротивления бетона для предельных состояний первой группы Rbt, МПа, при классе бетона по прочности на осевое растяжение | ||||||
| В t 0,8 | В t 1,2 | В t 1,6 | В t 2,0 | В t 2,4 | В t 2,8 | В t 3,2 | |
| Растяжение осевое Rbt | 0,62 | 0,93 | 1,25 | 1,55 | .1,85 | 2,15 | 2,45 |
5.1.10 В необходимых случаях расчетные значения прочностных характеристик бетона умножают на следующие коэффициенты условий работы γbi, учитывающие особенности работы бетона в, конструкции (характер нагрузки, условия.окружающей среды и т.д.):
а) γb1 - для бетонных и железобетонных конструкции, вводимый к расчетным значениям сопротивлений Rb и Rbt и учитывающий влияние длительности действия статической нагрузки:
γb1 = 1,0 - при непродолжительном (кратковременном) действии нагрузки;
γb1 = 0,9при продолжительном (длительном) действии нагрузки;
б) γb2 - для бетонных конструкций, вводимый к расчетным значениям сопротивления Rb и учитывающий характер разрушения таких конструкций;
γb2 = 0,9;
в) γb3 - для бетонных и железобетонных конструкций, бетонируемых в вертикальном положении, вводимый к расчетному значению сопротивления бетона Rb
γb3 = 0,9;
Влияние попеременного замораживания и оттаивания, а также отрицательных температур учитывают коэффициентом условий работы бетона γb4 ≤1,0 Для надземных конструкций, подвергаемых атмосферным воздействиям окружающей среды при расчетной температуре наружного воздуха в холодный период минус 40 °С и выше, принимают коэффициенту γb4 = 1,0. В остальных случаях значения коэффициента γb4 принимают в зависимости от назначения конструкции и условий окружающей среды согласно специальным указаниям.
Деформационные характеристики бетона
5.1.11 Основными деформационными характеристиками бетона являются значения:
- предельных относительных деформаций бетона при осевом сжатии и растяжении (при однородном напряженном состоянии бетона) ε b0 и ε bt0;
- начального модуля упругости Еb;
- коэффициента (характеристики) ползучести φb,cr
- коэффициента поперечной деформации бетона (коэффициента Пуассона) νb,P
- коэффициента линейной температурной деформации бетона αbt
5.1.12 Значения предельных относительных деформаций бетона принимают равными:
при непродолжительном действии нагрузки:
ε b0 = 0,002 - при осевом сжатии;
ε bt0 = 0,0001 - при осевом растяжении;
при продолжительном действии нагрузки - по таблице 5.6 в зависимости от относительной влажности окружающей среды.
5.1.13 Значения начального модуля упругости бетона при сжатии и растяжении принимают в зависимости от класса бетона по прочности на сжатие В согласно таблице 5.4.
При продолжительном действии нагрузки значения начального модуля деформаций бетона определяют по формуле
 ; ;
| (5.3) |
где φb,cr - коэффициент ползучести, принимаемый согласно 5.1.14.
5.1.14 Значения коэффициента ползучести бетона φb,cr принимают в зависимости от условий окружающей среды (относительной влажности воздуха) и класса бетона. Значения коэффициента ползучести бетона приведены в таблице 5.5.
5.1.15 Значение коэффициента поперечной деформации бетона допускается принимать νb,P = 0,2.
5.1.16 Значение коэффициента линейной температурной деформации бетона при изменении температуры от минус 40 до плюс 50 °С принимают: αbt = 1∙10-5 оС-1.
Таблица 5.4
| Значения начального модуля упругости бетона при сжатии и растяжении Еb, МПа∙10-3 при классе бетона по прочности на сжатие | ||||||||||
| В10 | В15 | В20 | В25 | В30 | В35 | В40 | В45 | В50 | В55 | В60 |
| 19,0 | 24,0 | 27,5 | 30,0 | 32,5 | 34,5 | 36,0 | 37,0 | 38,0 | 39,0 | 39,5 |
Таблица 5.5
| Относительная влажность воздуха окружающей среды, % | Значения коэффициента ползучести φb,cr при классе бетона на сжатие | ||||||||||
| В10 | В15 | В20 | В25 | В30 | В35 | В40 | В45 | В50 | В55 | В60 | |
| Выше 75 | 2,8 | 2,4 | 2,0 | 1,8 | 1,6 | 1,5 | 1,4 | 1,3 | 1,2 | 1,1 | 1,0 |
| 40-75 | 3,9 | 3,4 | 2,8 | 2,5 | 2,3 | 2,1 | 1,9 | 1,8 | 1,6 | 1,5 | 1,4 |
| Ниже 40 | 5,6 | 4,8 | 4,0 | 3,6 | 3,2 | 3,0 | 2,8 | 2,6 | 2,4 | 2,2 | 2,0 |
| Примечание - Относительную влажность воздуха окружающей среды. принимают по СНиП 23-01 как среднюю месячную относительную влажность наиболее теплого месяца для района строительства. |
Таблица 5.6
| Относительная влажность воздуха окружающей среды. % | Относительные деформации бетона при продолжительном действии нагрузки | |||||
| При сжатии | При растяжении | |||||
| ε b0 ∙103 | ε b2 ∙103 | ε b1,red ∙103 | ε bt0 ∙103 | ε bt2 ∙103 | ε bt1,red ∙103 | |
| Выше 75 | 3,0 | 4,2 | 2,4 | 0,21 | 0,27 | 0,19 |
| 40-75 | 3.4 | 4,8 | 2.8 | 0,24 | 0,31 | 0,22 |
| Ниже 40 | 4,0 | 5.6 | 3.4 | 0,28 | 0,36 | 0,26 |
| Примечание - Относительную влажность воздуха окружающей среды принимают по СНиП 23-01 как среднюю месячную относительную влажность наиболее теплого месяца для района строительства. |
Диаграммы состояния бетона


а - трехлинейная диаграмма состояния сжатого бетона;
б - двухлинейная диаграмма состояния сжатого бетона
Рисунок 5.1 - Диаграммы состояния сжатого бетона
5.1.17 В качестве расчетных диаграмм состояния бетона, определяющих связь между напряжениями и относительными деформациями, принимают трехлинейную и двухлинейную диаграммы (рисунок 5.1, а, б).
Диаграммы состояния бетона используют при расчете железобетонных элементов по нелинейной деформационной модели.
5.1.18 При трехлинейной диаграмме (рисунок 5.1, а) сжимающие напряжения бетона σ b в зависимости от относительных деформаций укорочения бетона ε b определяют по формулам:
при 0 ≤ ε b ≤ ε b1
 ; ;
| (5.4) |
при ε b1 < ε b < ε b0
 ; ;
| (5.5) |
при ε b0 ≤ ε b ≤ ε b2
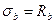 ; ;
| (5.6) |
Значения напряжений σ b1 принимают:
σ b1 = 0,6 Rb;
а значения относительных деформаций ε b1 принимают:
 ;
;
Значения относительных деформаций ε b2 принимают:
- при непродолжительном действии нагрузки ε b2 = 0,0035;
- при продолжительном действии нагрузки - по таблице 5.6.
Значения Rb, Eb и ε b0 принимают согласно 5.1.9, 5.1.10, 5.1.12, 5.1.13.
5.1.19 При двухлинейной диаграмме (рисунок 5.1, б) сжимающие напряжения бетона σ b в зависимости от относительных деформаций ε b определяют по формулам:
при 0 ≤ ε b ≤ ε b1, где 
 ; ;
| (5.7) |
при ε b1 ≤ ε b ≤ ε b2
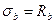 ; ;
| (5.8) |
Значения приведенного модуля деформации бетона Eb,red принимают:
 ; ;
| (5.9) |
Значения относительных деформаций ε b1,red принимают:
- при непродолжительном действии нагрузки ε b1,red = 0,0015;
- при продолжительном действии нагрузки - по таблице 5.6.
Значения Rb, ε b2 принимают, как в 5.1.18.
5.1.20 Растягивающие напряжения бетона σ bt в зависимости от относительных деформаций ε bt определяют по приведенным в 5.1.18 и 5.1.19 диаграммам. При этом расчетные значения сопротивления бетона сжатию Rb заменяют на расчетные значения сопротивления бетона растяжению Rbt согласно 5.1.9, 5.1.10, значения начального модуля упругости Ebt, определяют согласно 5.1.13, значения относительной деформации ε bt0 принимают согласно 5.1.12, значения относительной деформации ε bt2 принимают при непродолжительном действии нагрузки ε bt2 = 0,00015, при продолжительном действии нагрузки - по таблице 5.6. Для двухлинейной диаграммы принимают ε bt1,red = 0,00008 - при непродолжительном действии нагрузки, а при продолжительном - по таблице 5.6; значения Ebt,red определяют по формуле (5.9), подставляя в нее Rbt и ε bt1,red.
5.1.21 При расчете прочности железобетонных элементов по нелинейной деформационной модели для определения напряженно-деформированного состояния сжатой зоны бетона используют диаграммы состояния сжатого бетона, приведенные в 5.1.18 и 5.1.19 с деформационными характеристиками, отвечающими непродолжительному действию нагрузки. При этом в качестве наиболее простой используют двухлинейную диаграмму состояния бетона.
5.1.22 При расчете образования трещин в железобетонных конструкциях по нелинейной деформационной модели для определения напряженно-деформированного состояния сжатого и растянутого бетона используют трехлинейную диаграмму состояния бетона, приведенную в 5.1.18 и 5.1.20 с деформационными характеристиками, отвечающими непродолжительному действию нагрузки. Двухлинейную диаграмму (5.1.19) как наиболее простую используют для определения напряженно-деформированного состояния растянутого бетона при упругой работе сжатого бетона.
5.1.23 При расчете деформаций железобетонных элементов по нелинейной деформационной модели при отсутствии трещин для определения напряженно-деформированного состояния в сжатом и растянутом бетоне используют трехлинейную диаграмму состояния бетона с учетом непродолжительного и продолжительного действия нагрузки. При наличии трещин для определения напряженно-деформированного состояния сжатого бетона помимо указанной выше диаграммы используют как наиболее простую двухлинейную диаграмму состояния бетона с учетом непродолжительного и продолжительного действия нагрузки.
5.1.24 При расчете раскрытия нормальных трещин по нелинейной деформационной модели для определения напряженно-деформированного состояния в сжатом бетоне используют диаграммы состояния, приведенные в 5.1.18 и 5.1.19 с учетом непродолжительного действия нагрузки. При этом в качестве наиболее простой используют двухлинейную диаграмму состояния бетона.
5.1.25 Влияние попеременного замораживания и оттаивания, а также отрицательных температур на деформационные характеристики бетона учитывают коэффициентом условий работы γbt ≤ 1,0. Для надземных конструкций, подвергаемых атмосферным воздействиям окружающей среды при расчетной температуре наружного воздуха в холодный период минус 40 °С и выше, принимают коэффициент γbt = 1,0. В остальных случаях значения коэффициента γbt, принимают в зависимости от назначения конструкций и условий окружающей среды.
Date: 2015-10-21; view: 449; Нарушение авторских прав