Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Регіональний пошук. Методи
|
|
Задача. На заданій множині S із N точок задано запитний регіон R. Знайти підмножину точок множини S (або їх кількість), які містяться в регіоні R.
Одновимірний регіональний пошук. Множина з N точок на осі x являє файл, а запитним регіоном є відрізок [ x',x" ] (який називається x - регіоном). Ефективний регіональний пошук реалізується через метод, який базується на методі двійкового пошуку. Структура даних, яка забезпечує вказану дію, є прошите двійкове дерево, т.т. таке збалансоване двійкове дерево, листки якого додатково зв’язані у списку, який виражає порядок абсцис; дерево і список обробляються на фазах відповідногопошуку й вибірки. Оцінки: оптимальна як по часу запиту q(logN+k), так і по пам’яті q(N).
Алгоритм 2-D-дерева. (складність попередньої обробки: 
, пошуку: 
). Означення. Назвемо узагальненим прямокутником таку область на площині, яка визначена декартовим добутком [x1, x2]´[y1,y2] x- інтервалу - [x1, x2] та у – інтервалу - [y1,y2], включаючи граничні випадки, коли в довільній комбінації допускається: x1= - ¥, x2 = ¥, y1= - ¥, y2 = ¥.
Нехай задана множина S із N точок на площині. Для побудови структури даних, яка називається “2-D дерево” використовується схема “розподіляй та володарюй” суть якої полягає в рекурсивному розбиті площини на прямокутники R (v), означені вище. Результатом розбиття є бінарне дерево пошуку, вузлами якого є точки із заданої множини S на площині.
Проектуються усі точки множини S на вісі ОХ та ОУ. Знаходиться медіана списку точок впорядкованих по х, проводиться вертикаль. Точка буде коренем шуканого дерева і розіб'є список на дві рівнопотужні підмножини, для яких існують списки вопрядковані по у. Для них визначаються медіани і будуються горизонталі. Ті точки будуть наступними вузлами шуканого дерева.Для зручності при побудові шуканого дерева ведемо позначення для вузлів трьох різних типів: кружки - не листові вузли з вертикальною лінією розрізу, квадрати - не листові вузли з горизонтальною лінією розрізу, точки - листки.
Метод дерева регіонів. (складність попередньої обробки: 
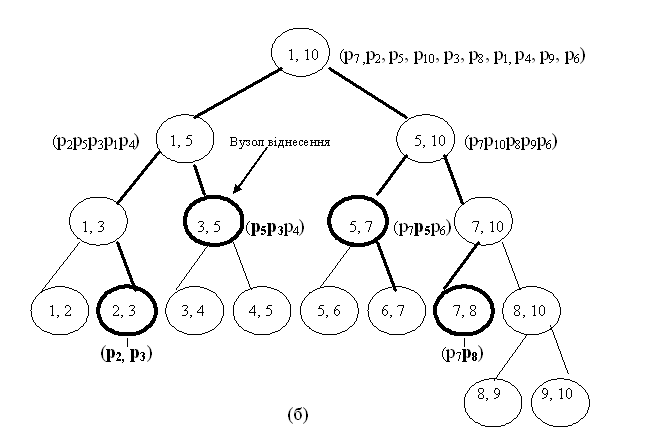
, пошук: 
). Будується дворівнева структура даних (дерево регіонів), перший рівень якої – дерево відрізків по одній із координат (наприклад х), а другий – вузли дерева відрізків прошиті упорядкованими списками по іншій координаті (наприклад у). На побудованому дереві регіонів виконується операції вставки інтервалу (проекція запитного регіону на вісь ОХ), що дозволяє визначити вузли віднесення. Далі у вузлах віднесення застосовується дихотомія пошуку по іншій координаті (у).
Метод прямого доступу: Площина розбивається на комірки прямими, що проходять через всі дані точки (пари комірок утворюються класи еквівалентності відносно результатів пошуку). Для кожнох пари комірок встановлюється відповідна множина точок. Для співставлення точки одній комірці - двійковий пошук по x, у координатам. Звертання до файлу - константа. Пам'ять O(N5)
Date: 2015-09-24; view: 354; Нарушение авторских прав